มีน้อง ๆ คนไหนกำลังเรียนอยู่ชั้น ม.6 หรือกำลังเตรียมตัวเลื่อนชั้น แล้วกำลังกังวลว่าคณิต ม.6 จะยากมาก ๆ กันอยู่หรือเปล่าา ต้องบอกก่อนว่าเนื้อหาคณิต ม.6 เป็นเนื้อหาที่ต่อยอดมาจากคณิต ม.4 กับคณิต ม.5 นี่แหละ
ซึ่งสรุปเนื้อหาคณิต ม.6 ที่พี่เอามาฝากวันนี้ก็เป็นเรื่อง ลำดับและอนุกรม นั่นเองง พร้อมไขข้อสงสัย ลำดับเลขคณิต, ลำดับเรขาคณิต, อนุกรมเลขคณิต, อนุกรมเรขาคณิต คืออะไร ? แถมพี่ยังมีตัวอย่างโจทย์พร้อมวิธีทำเพื่อให้ทุกคนเข้าใจง่าย ๆ ด้วยยยยย ไปดูกันเล้ย
ความหมายของลำดับ
บทนิยาม
ลำดับ (sequence) คือ ฟังก์ชันที่มีโดเมนเป็นเซต \left \{ 1,2,3,…,n \right \} หรือมีโดเมนเป็นเซตของจำนวนเต็มบวก
ในการเขียนแสดงลำดับ
เรียก a_{1} ว่า พจน์ที่ 1 ของลำดับ
เรียก a_{2} ว่า พจน์ที่ 2 ของลำดับ
เรียก a_{3} ว่า พจน์ที่ 3 ของลำดับ
\vdots
และเรียก a_{n} ว่า พจน์ที่ n ของลำดับ หรือพจน์ทั่วไปของลำดับ
ตัวอย่างที่ 1 จงเขียนสี่พจน์แรกของลำดับ a_{n}= 2n+1
วิธีทำ
\\a_{1}= 2\left ( 1 \right )+1= 3
\\
a_{2}= 2\left ( 2 \right )+1= 5
\\
a_{3}= 2\left ( 3\right )+1= 7
\\
a_{4}= 2\left ( 4 \right )+1= 9
ดังนั้น สี่พจน์แรกของลำดับ คือ 3, 5, 7, 9
ลำดับจำกัดและลำดับอนันต์
ลำดับจำกัด (finite sequence) คือ ลำดับที่มีโดเมนเป็นเซต \left \{ 1,2,3,…,n \right \} ซึ่งเขียนแสดงลำดับจำกัด ด้วย a_{1},a_{2},a_{3},…,a_{n}
ลำดับอนันต์ (infinite sequence) คือ ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก ซึ่งเขียนแสดงลำดับอนันต์ ด้วย a_{1},a_{2},a_{3},…,a_{n},…
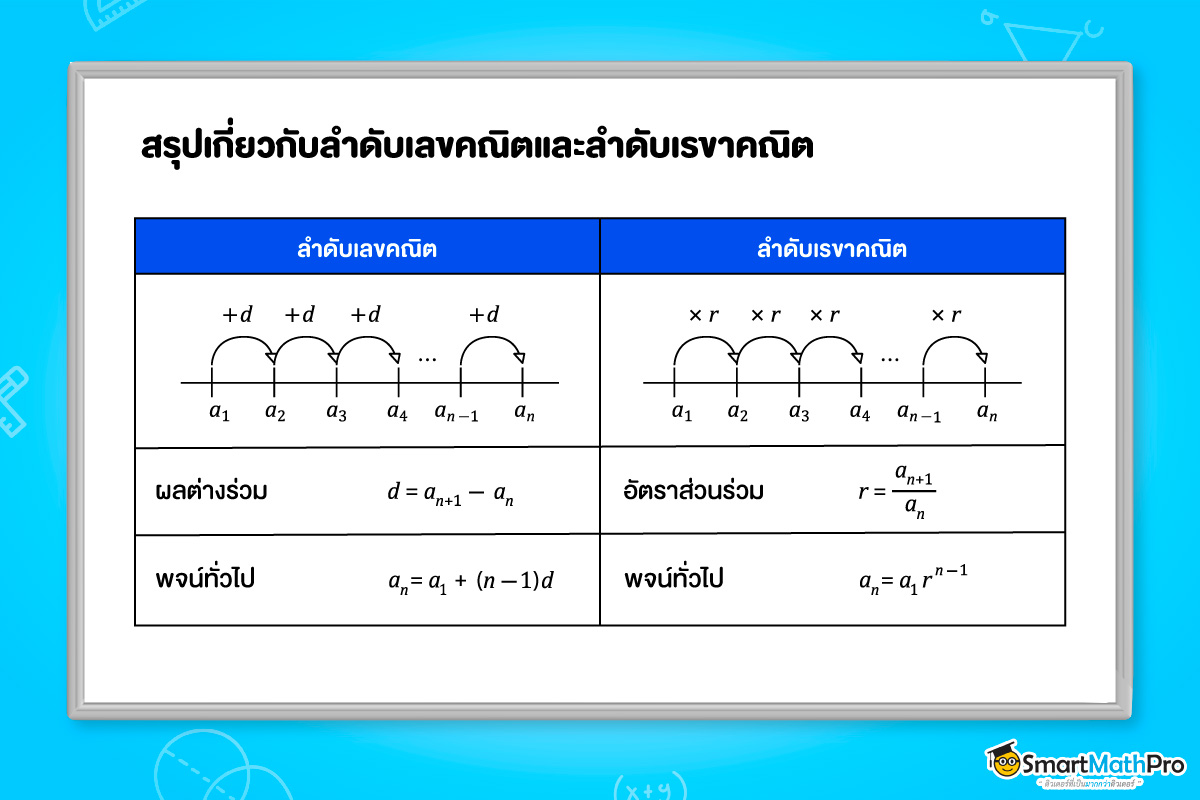
ลำดับเลขคณิต
บทนิยาม
ลำดับเลขคณิต (arithmetic sequence) คือ ลำดับซึ่งมีผลต่างที่ได้จากการนำพจน์ที่ n+1 ลบด้วยพจน์ที่ n เป็นค่าคงตัวที่เท่ากัน
สำหรับทุกจำนวนเต็มบวก n และเรียกค่าคงตัวที่เป็นผลต่างนี้ว่า ผลต่างร่วม (common difference:d)
ถ้าลำดับ a_{1},a_{2},a_{3},…,a_{n}เป็นลำดับเลขคณิต แล้ว d=a_{n+1}-a_{n} สำหรับทุกจำนวนเต็มบวก n
ตัวอย่างที่ 2 จงหาผลต่างร่วม (d) ของลำดับเลขคณิตต่อไปนี้
1) 2,5,8,…
จะได้ว่า d=3
2) 2,2,2,…
จะได้ว่า d=0
3) 15,10,5,0,…
จะได้ว่า d=-5
สูตรพจน์ทั่วไปของลำดับเลขคณิต
ให้ a_{1},a_{2},a_{3},…,a_{n} เป็นลำดับเลขคณิต จะมีพจน์ทั่วไปของลำดับ คือ
a_{n}=a_{1}+\left ( n-1 \right )d
ตัวอย่างที่ 3 จงหาพจน์ทั่วไปของลำดับเลขคณิต 3,7,11,…
วิธีทำ
จาก a_{1}=3 และ a_{2}=7
จะได้ว่า d=a_{2}-a_{1}=7-3=4
จาก a_{n}=a_{1}+\left ( n-1 \right )d
จะได้ว่า a_{n}=3+(n-1)(4)
\\a_{n}=3+4n-4
\\a_{n}=4n-1
ดังนั้น พจน์ทั่วไปของลำดับเลขคณิต 3,7,11,… คือ a_{n}=4n-1
ลำดับเรขาคณิต
บทนิยาม
ลำดับเรขาคณิต (geometric sequence) คือ ลำดับซึ่งมีอัตราส่วนของพจน์ที่ n+1 ต่อพจน์ที่ n เป็นค่าคงตัวที่เท่ากัน สำหรับทุกจำนวนเต็มบวก n และเรียกค่าคงตัวที่เป็นอัตราส่วนนี้ว่า อัตราส่วนร่วม (common ratio: r)
ถ้าลำดับ a_{1},a_{2},a_{3},…,a_{n} เป็นลำดับเรขาคณิต แล้ว r=\frac{a_{n+1}}{a_{n}} สำหรับทุกจำนวนเต็มบวก n
ตัวอย่างที่ 4 จงหาอัตราส่วนร่วม (r) ของลำดับเรขาคณิตต่อไปนี้
1) 2,4,8,…
จะได้ว่า r=2
2) \frac{1}{3},\frac{1}{9},\frac{1}{27},…
จะได้ว่า r=\frac{1}{3}
3) 3,3,3,…
จะได้ว่า r=1
สูตรพจน์ทั่วไปของลำดับเรขาคณิต
ให้ a_{1},a_{2},a_{3},…,a_{n} เป็นลำดับเรขาคณิต จะมีพจน์ทั่วไปของลำดับ คือ
a_{n}=a_{1}r^{n-1}
ตัวอย่างที่ 5 จงหาพจน์ทั่วไปของลำดับเรขาคณิต 1,4,16,…
วิธีทำ
จาก a_{1}=1 และ a_{2}=4
จะได้ว่า r=\frac{a_{2}}{a_{1}}=\frac{4}{1}=4
จาก a_{n}=a_{1}r^{n-1}
จะได้ว่า a_{n}=(1)(4)^{n-1}
a_{n}=4^{n-1}
ดังนั้น พจน์ทั่วไปของลำดับเรขาคณิต 1,4,16,… คือ a_{n}=4^{n-1}
ลิมิตของลำดับอนันต์
ความหมายของลิมิตของลำดับอนันต์
บทนิยาม
ให้ a_{1},a_{2},a_{3},…,a_{n},… เป็นลำดับอนันต์ ถ้า n มากขึ้นโดยไม่มีที่สิ้นสุด
แล้ว a_{n} เข้าใกล้หรือเท่ากับจำนวนจริง L เพียงจำนวนเดียวเท่านั้น จะเขียน
a_{n}=L และจะเรียก L ว่า ลิมิตของลำดับ
ลำดับลู่เข้า คือ ลำดับอนันต์ที่มีลิมิต และลำดับลู่ออก คือ ลำดับอนันต์ที่ไม่ใช่ลำดับลู่เข้า
ตัวอย่างที่ 6 จงพิจารณาว่าลำดับต่อไปนี้เป็นลำดับลู่เข้าหรือลำดับลู่ออก
1) 3,3,3,…
ตอบ เป็นลำดับลู่เข้า
2) -6,-3,0,…
ตอบ เป็นลำดับลู่ออก
3) a_{n}=\frac{1}{4n}
ตอบ เป็นลำดับลู่เข้า
สมบัติของลิมิตของลำดับอนันต์
ให้ a_{n},b_{n},t_{n} เป็นลำดับของจำนวนจริง A,B เป็นจำนวนจริง และ c เป็นค่า
คงตัวใด ๆ โดยที่ a_{n}=A และ b_{n}=B จะได้ว่า
• ถ้า t_{n}=c ทุกจำนวนเต็มบวก n แล้ว t_{n}= c=c
• ca_{n}=c a_{n}=cA
• \left ( a_{n}\pm b_{n} \right )= a_{n}\pm b_{n}=A\pm B
• \left ( a_{n}\cdot b_{n} \right )= a_{n}\cdot b_{n}=A\cdot B
• ถ้า b_{n}\neq 0 ทุกจำนวนเต็มบวก n และ B\neq 0 แล้ว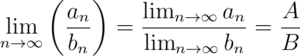 
• ให้ m เป็นจำนวนเต็มที่มากกว่า 1 แล้ว 
ตัวอย่างที่ 7 จงหาลิมิตของลำดับ เมื่อ a_{n}=\frac{3n-2}{n}
วิธีทำ\left ( \frac{3n-2}{n} \right )
= \left ( \frac{3n}{n} -\frac{2}{n}\right )
= \frac{3n}{n}- \frac{2}{n}
= 3 – \frac{2}{n}
=3-0=3
อนุกรมจำกัด
ความหมายของอนุกรมจำกัด
บทนิยาม
ถ้า a_{1},a_{2},a_{3},…,a_{n} เป็นลำดับจำกัดที่มี n พจน์ จะเรียกการเขียนแสดงการบวกของทุกพจน์
ของลำดับในรูป a_{1}+a_{2}+a_{3}+\cdots+a_{n} ว่า อนุกรมจำกัด (finite series)
เราจะเรียก a_{n} ว่า พจน์ที่ n ของอนุกรม และให้ S_{n} แทนผลบวก n พจน์แรกของอนุกรม
พิจารณาลำดับต่อไปนี้
1,3,5,7,9,11
จะได้ว่า
S_{6}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+a_{6}
=1+3+5+7+9+11
=36
อนุกรมเลขคณิต
จากสองสูตรของอนุกรมเลขคณิต จะเห็นว่าสูตรแรกเราจะใช้เมื่อเราทราบพจน์แรกและพจน์ที่ n ส่วนสูตรที่สองเราจะใช้เมื่อไม่ทราบพจน์ที่ n
ตัวอย่างที่ 8 จงหาผลบวกของอนุกรมเลขคณิต 4+7+10+\cdots +31
วิธีทำ
ขั้นตอนที่ 1 หาค่า n
จาก a_{1}=4,a_{n}=31 และ d=7-3=4
จากสูตรพจน์ทั่วไปของลำดับเลขคณิตคือ a_{n}=a_{1}+\left ( n-1 \right )d
จะได้ว่า \\31=4+(n-1)
\\31=4+3n-3
\\30=3n
\\n=10
ขั้นตอนที่ 2 หาผลบวกของอนุกรมเลขคณิต
จากสูตรอนุกรมเลขคณิต S_{n}=\frac{n}{2}\left ( a_{1}+a_{n} \right )
จะได้ว่า S_{10}=\frac{10}{2}\left ( 4+31 \right )=5(35)=175
อนุกรมเรขาคณิต
น้องจะเห็นว่าสูตรเรขาคณิตมี 2 สูตรซึ่งเราแยกออกมาเป็น 2 สูตรเพื่อให้ตัวส่วนเป็นบวกและง่ายต่อการคิด แต่จริง ๆ แล้วเราสามารถจำสูตรเดียวได้เลยน้า ได้ค่าเท่ากันเลย
ตัวอย่างที่ 9 จงหาผลบวกของอนุกรมเรขาคณิต 800+400+200+\cdots +25
วิธีทำ
ขั้นตอนที่ 1 หาค่า n
จาก a_{1}=800 และ r=\frac{400}{800}=\frac{1}{2}
จากสูตรพจน์ทั่วไปของลำดับเรขาคณิตคือ a_{n}=a_{1}r^{n-1}
จะได้ว่า \\25=800\left ( \frac{1}{2} \right )^{n-1}
\\\frac{1}{32}=\left ( \frac{1}{2} \right )^{n-1}
\\\left ( \frac{1}{2} \right )^{5}=\left ( \frac{1}{2} \right )^{n-1}
5=n-1
n=6
ขั้นตอนที่ 2 หาผลบวกของอนุกรมเรขาคณิต
จากสูตรอนุกรมเรขาคณิต S_{n}=\frac{a_{1}(1-r^{n})}{1-r}
จะได้ว่า S_{6}=\frac{800(1-(\frac{1}{2})^{6})}{1-\frac{1}{2}}=\frac{800(\frac{63}{64})}{\frac{1}{2}}=1575
อนุกรมอนันต์
ความหมายของอนุกรมอนันต์
อนุกรมอนันต์ คือ อนุกรมของลำดับอนันต์
กำหนดอนุกรมอนันต์ a_{1}+a_{2}+a_{3}+\cdots +a_{n}+\cdots
ให้ S_{1},S_{2},S_{3},…,S_{n},… เป็นลำดับของผลบวกย่อยของอนุกรมนี้
อนุกรมลู่เข้า ก็ต่อเมื่อ S_{n} เป็นลำดับลู่เข้า หรือกล่าวได้ว่า S_{n}=S เมื่อ S เป็นจำนวนจริง
และเรียก S ว่าผลบวกของอนุกรมอนันต์
อนุกรมลู่ออก ก็ต่อเมื่อ S_{n} เป็นลำดับลู่ออก หรือกล่าวได้ว่า S_{n} ไม่มีค่า
อนุกรมเรขาคณิตอนันต์
ตัวอย่างที่ 10 จงพิจารณาว่าอนุกรม 1+\frac{1}{3}+\frac{1}{9}+\cdots +\frac{1}{3^{n-1}}+\cdots เป็นอนุกรมลู่เข้าหรืออนุกรมลู่ออก ถ้าเป็นอนุกรมลู่เข้า จงหาผลบวกของอนุกรม
วิธีทำ
พิจารณา 1+\frac{1}{3}+\frac{1}{9}+\cdots +\frac{1}{3^{n-1}}+\cdots
จะได้ว่า r=\frac{1}{3} ซึ่ง \left | r \right |=\left | \frac{1}{3} \right |=\frac{1}{3}<1
ดังนั้น อนุกรมนี้เป็นอนุกรมลู่เข้า
โดยผลบวกของอนุกรมเท่ากับ \frac{a_{1}}{1-r}=\frac{1}{1-\frac{1}{3}}=\frac{1}{\frac{2}{3}}=\frac{3}{2}
อนุกรมรูปแบบพิเศษ
อนุกรมเทเลสโคปิก
อนุกรมเทเลสโคปิก คือ อนุกรมที่สามารถจัดให้อยู่ในรูปของ a_{n}-a_{n+1} ได้ ให้น้อง ๆ จัดรูปให้เป็นเศษส่วนย่อย โดยมีสูตรคือ
\frac{1}{ab}=(\frac{1}{b-a})(\frac{1}{a}-\frac{1}{b})
เราลองไปดูการหาผลบวกของอนุกรมเทเลสโคปิก และใช้สูตรผ่านตัวอย่างต่อไปนี้กัน
ตัวอย่างที่ 11 จงหาผลบวกของอนุกรม \frac{1}{3\times 6}+\frac{1}{6\times 9}+\frac{1}{9\times 12}+\cdots +\frac{1}{27\times 30}
วิธีทำ \frac{1}{3\times 6}+\frac{1}{6\times 9}+\frac{1}{9\times 12}+\cdots +\frac{1}{27\times 30}
=(\frac{1}{3})(\frac{1}{3}-\frac{1}{6})+(\frac{1}{3})(\frac{1}{6}-\frac{1}{9})+(\frac{1}{3})(\frac{1}{9}-\frac{1}{12})+\cdots +(\frac{1}{3})(\frac{1}{27}-\frac{1}{30})
=(\frac{1}{3})[(\frac{1}{3}-\frac{1}{6})+(\frac{1}{6}-\frac{1}{9})+(\frac{1}{9}-\frac{1}{12})+\cdots +(\frac{1}{27}-\frac{1}{30})]
=(\frac{1}{3})(\frac{1}{3}-\frac{1}{30})
=(\frac{1}{3})(\frac{9}{30})
=\frac{1}{10}
อนุกรมผสม
อนุกรมผสมมีหลายรูปแบบ เช่น อนุกรมผสมระหว่างอนุกรมเลขคณิตกับอนุกรมเรขาคณิต อนุกรมผสมระหว่างอนุกรมเลขคณิตกับอนุกรมอนันต์ เป็นต้น และด้วยรูปแบบที่ไม่ตายตัวของอนุกรมผสม ทำให้วิธีการหาค่าของอนุกรมผสมมีหลากหลาย แต่ไม่ยากเกินความสามารถน้อง ๆ แน่นอนนน
ตัวอย่างที่ 12 จงหาผลบวกของอนุกรม \frac{1}{2}+\frac{3}{4}+\frac{5}{8}+\frac{7}{16}+\frac{9}{32}+\frac{11}{64}
วิธีทำ กำหนดให้ S=\frac{1}{2}+\frac{3}{4}+\frac{5}{8}+\frac{7}{16}+\frac{9}{32}+\frac{11}{64}
นำ \frac{1}{2} คูณทั้งสองข้างของสมการ
จะได้ว่า \frac{1}{2}S=\frac{1}{4}+\frac{3}{8}+\frac{5}{16}+\frac{7}{32}+\frac{9}{64}+\frac{11}{128}
ดังนั้น
S-\frac{1}{2}S=\left (\frac{1}{2}+\frac{3}{4}+\frac{5}{8}+\frac{7}{16}+\frac{9}{32}+\frac{11}{64} \right )-\left (\frac{1}{4}+\frac{3}{8}+\frac{5}{16}+\frac{7}{32}+\frac{9}{64}+\frac{11}{128} \right )
\frac{1}{2}S=\frac{1}{2}+\frac{2}{4}+\frac{2}{8}+\frac{2}{16}+\frac{2}{32}+\frac{2}{64}-\frac{11}{128}
เนื่องจาก \frac{2}{4}+\frac{2}{8}+\frac{2}{16}+\frac{2}{32}+\frac{2}{64} เป็นอนุกรมเรขาคณิตที่มี a_{1}=\frac{2}{4}=\frac{1}{2},r=\frac{1}{2} และ n=5
และผลบวก n พจน์แรกของอนุกรมเรขาคณิต คือ S_{n}=\frac{a_{1}(1-r^{n})}{1-r}
ดังนั้น
\frac{2}{4}+\frac{2}{8}+\frac{2}{16}+\frac{2}{32}+\frac{2}{64}=\frac{\frac{1}{2}(1-(\frac{1}{2})^{5})}{1-\frac{1}{2}}=\frac{31}{32}
จะได้ว่า \frac{1}{2}S=\frac{1}{2}+\frac{31}{32}-\frac{11}{128}=\frac{177}{128}
ดังนั้น S=(\frac{177}{128})(2)=\frac{177}{64}
สัญลักษณ์แสดงการบวก
เพื่อความสะดวกในการเขียนอนุกรม เราจะใช้อักษรกรีก \sum (อ่านว่า ซิกมา) เป็นสัญลักษณ์แสดงการบวก
สามารถเขียนได้เป็น \sum_{i=1}^{n}a_{i} หรือ \sum_{i=1}^{\infty }a_{i} แต่ไม่จำเป็นต้องเป็นตัวแปร i น้า และสามารถเริ่มต้นที่ใด ๆ ก็ได้ ไม่จำเป็นต้องเริ่มที่ 1 เช่น \sum_{n=0}^{3}(n+2)=2+3+4+5
สมบัติของซิกมา
กำหนดให้ n เป็นจำนวนเต็มบวกใด ๆ จะได้ว่า
1) \sum_{i=1}^{n}c=nc เมื่อ c เป็นค่าคงตัว
2) \sum_{i=1}^{n}ca_{i}=c\sum_{i=1}^{n}a_{i}เมื่อ c เป็นค่าคงตัว
3) \sum_{i=1}^{n}(a_{i}\pm b_{i})=\sum_{i=1}^{n}a_{i}\pm \sum_{i=1}^{n}b_{i}
จากสมบัติของซิกมา จะเห็นว่าเราสามารถกระจายซิกมาเข้าไปในการบวกและลบได้ แต่เราไม่สามารถกระจายเข้าไปในการคูณและการหารได้ ระวังด้วยน้า
ตัวอย่างที่ 13 จงหา \sum_{i=1}^{4}(i^{2}-i)
วิธีทำ \sum_{i=1}^{4}(i^{2}-i)=\sum_{i=1}^{4}i^{2}-\sum_{i=1}^{4}i
=(1+4+9+16)-(1+2+3+4)
=30-10
=20
ดอกเบี้ยและมูลค่าเงิน
ในบทนี้ เราสามารถนำความรู้เรื่องลำดับและอนุกรมมาประยุกต์ใช้ในการคิดดอกเบี้ยและมูลค่าเงินได้ด้วย ลองไปดูกันเลย
ดอกเบี้ยทบต้น
เราจะใช้ทั้งสองสูตรนี้ในการคำนวณหาเงินรวม โดยสูตรที่ต่างกันขึ้นกับว่าเป็นการคิดดอกเบี้ยทบต้นปีละ 1 ครั้ง หรือปีละหลายครั้ง
มูลค่าของเงิน
ค่างวด
เงินฝาก
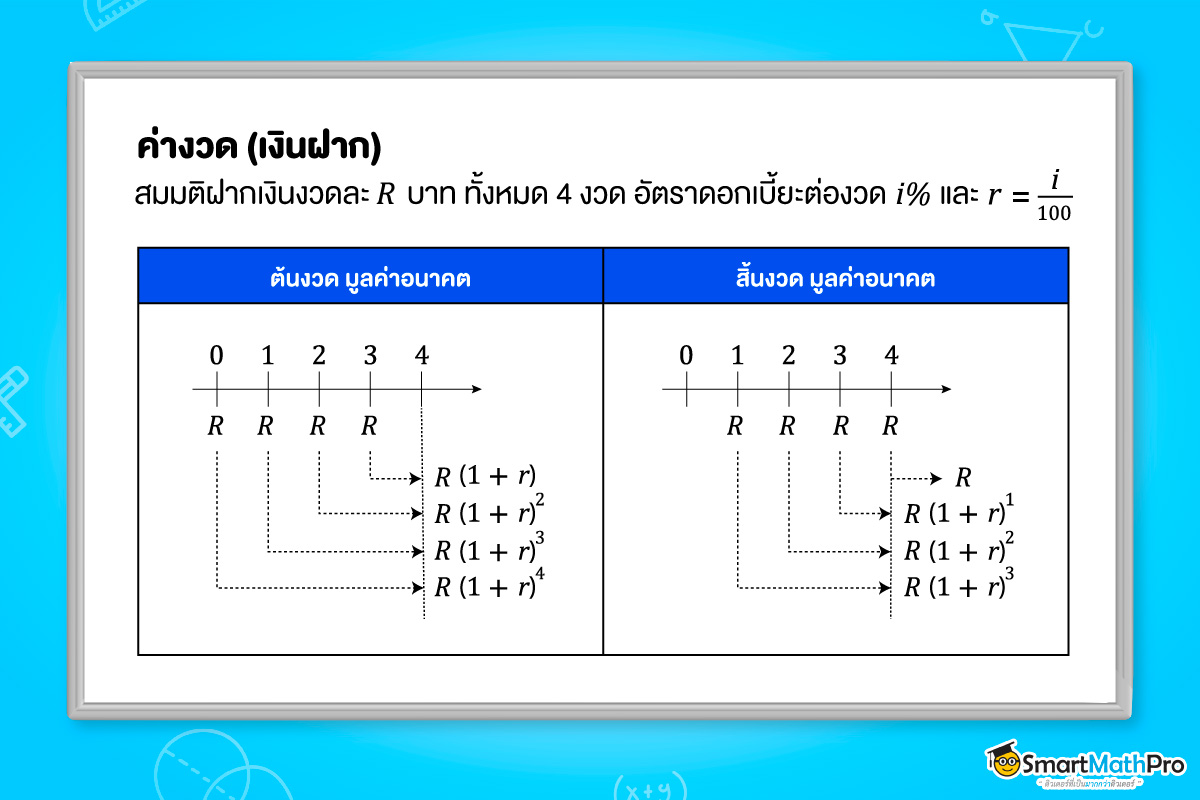
ถ้ารวมเงินทั้งหมดเข้าด้วยกัน จะเรียกว่า เงินรวม ใช้ในเรื่องการฝากประจำ
จากรูป เงินรวมของต้นงวด: R(1+r)+R(1+r)^{2}+R(1+r)^{3}+R(1+r)^{4}
เงินรวมของสิ้นงวด: R+R(1+r)+R(1+r)^{2}+R(1+r)^{3}
ลองไปดูการคิดเงินรวมจากตัวอย่างต่อไปนี้กัน
ตัวอย่างที่ 14 จอร์จเก็บเงินเดือนละ 2,000 บาท เป็นเวลา 6 เดือน โดยฝากธนาคารทุกต้นเดือน อยากทราบว่าเมื่อสิ้นเดือนที่ 6 จอร์จจะมีเงินเก็บเท่าใด หากธนาคารคิดดอกเบี้ย 24% ต่อปี และดอกเบี้ยคิดทบต้นทุกเดือน
วิธีทำ i=\frac{24}{12}=2 จะได้ i=\frac{2}{100}=0.02
S_{6}=\frac{2000(1.02)(1.02^{6}-1)}{1.02-1}=12,868.57
ดังนั้น จอร์จจะมีเงินเก็บ 12,868.57 บาท
ตัวอย่างที่ 15 จุ้ยเก็บเงินเดือนละ 2,000 บาท เป็นเวลา 6 เดือน โดยฝากธนาคารทุกสิ้นเดือน อยากทราบว่าเมื่อสิ้นเดือนที่ 6 จุ้ยจะมีเงินเก็บเท่าใด หากธนาคารคิดดอกเบี้ย 6 ต่อปี และดอกเบี้ยคิดทบต้นทุกเดือน
วิธีทำ i=\frac{24}{12}=2 จะได้ i=\frac{2}{100}=0.02
S_{6}=\frac{2000(1.02^{6}-1)}{1.02-1}=12,616.24
ดังนั้น จุ้ยจะมีเงินเก็บ 12,616.24 บาท
จากตัวอย่างที่ 14 และ 15 เราจะได้ว่าการฝากเงินที่เงินฝาก ระยะเวลาการฝาก ดอกเบี้ยเท่ากัน แต่ช่วงเวลาในการฝากต่างกัน คือต้นงวดและสิ้นงวด จะได้เงินรวมที่ไม่เท่ากัน
เงินผ่อน
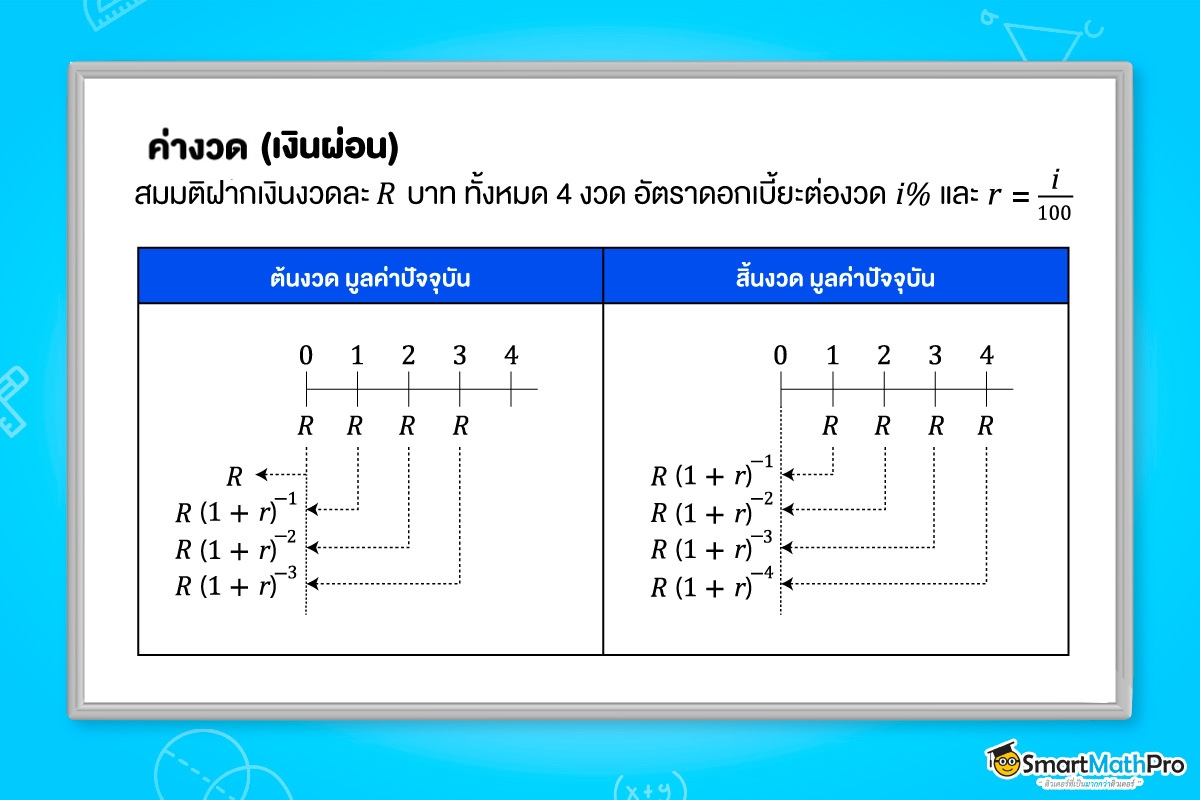
ถ้ารวมเงินทั้งหมดเข้าด้วยกัน จะเรียกว่า มูลค่าปัจจุบันของเงินผ่อนทั้งหมดใช้ในเรื่องการผ่อนสินค้า
เช่น เงินผ่อนของต้นงวด : R+R(1+r)^{-1}+R(1+r)^{-2}+R(1+r)^{-3}
เงินผ่อนของสิ้นงวด : R(1+r)^{-1}+R(1+r)^{-2}+R(1+r)^{-3}+R(1+r)^{-4}
ดูคลิปติวฟรี ลำดับและอนุกรม ม.6
คลิปติว ลำดับและอนุกรม ม.6 จาก SmartMathPro
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
เป็นยังไงบ้างง สำหรับสรุปเนื้อหาเรื่องลำดับและอนุกรม ม.6 ที่พี่เอามาฝากทุกคน อย่างที่น้อง ๆ เห็นด้านบนเลยว่าเรื่องนี้สามารถเอาไประยุกต์ใช้ในการคิดดอกเบี้ยและมูลค่าเงินได้ด้วย ทำให้เวลาทำโจทย์อาจจะต้องอาศัยการวิเคราะห์ประมาณหนึ่ง พี่แนะนำว่าให้ทบทวนโดยการทำโจทย์บ่อย ๆ น้า จะได้คล่องมือ ใครไม่รู้จะไปหาโจทย์จากไหนมาฝึกก็สามารถเข้าไปดาวน์โหลดข้อสอบลำดับและอนุกรม ม.6 กันได้เลยย
ส่วนน้อง ๆ ที่คิดว่าตัวเองยังไม่แม่นเนื้อหาบทนี้ ฝึกทำโจทย์แล้วก็ยังไม่เข้าใจ แนะนำให้เสริมพื้นฐานบทที่ควรรู้ก่อนเรียนอย่างบทเลขยกกำลังหรือฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึมเพิ่ม อาจจะช่วยทำให้เข้าใจในเรื่อง ลำดับและอนุกรมมากขึ้น ค่อย ๆ ทบทวนไป พี่เชื่อว่าทุกคนทำได้แน่นอนน !!
แต่ถ้าอยากตัวช่วยพี่ก็มีคอร์สมาแนะนำด้วยยยย เป็นคอร์สเสริมเกรดคณิตม.ปลาย ที่น้อง ๆ สามารถเลือกจัดแพ็กเองได้ โดยในคอร์ส พี่สอนเนื้อหาละเอียด อิงตามหลักสูตร สสวท. ปีล่าสุด แถมพาตะลุยโจทย์ และแบบฝึกหัดเพียบบบ ใครสนใจ คลิก ไปดูรายละเอียดได้น้าา
บทความ แนะนำ
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
สถิติ ม.6 สรุปเนื้อหาสถิติและข้อมูล พร้อมโจทย์แบบจัดเต็ม ! - SmartMathPro
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
A-Level คณิต 1, A-Level คณิต 2 TCAS67 สอบอะไรบ้าง? อัปเดตล่าสุด
ข้อสอบ A-Level คณิต 1 และคณิต 2 67 ออกอะไรบ้าง ? พร้อมแจกบทน่าเก็บ
A Level คณิตศาสตร์ 1 กับ 2 ต่างกันยังไง? ยื่นคณะไหนได้บ้าง?
บทความ แนะนำ
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม ได้ที่ Line : @smartmathpronews
รวมถึงข่าวสารต่าง ๆ อัปเดตอย่างเรียลไทม์
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
Twitter : @PanSmartMathPro
Tiktok : @pan_smartmathpro
