สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!

พอพูดถึงเรื่องการแก้สมการ น้อง ๆ หลายคนอาจจะคุ้นเคยกับเรื่องสมการเชิงเส้นตัวแปรเดียวที่เราเคยเรียนกันมา
ตอนม.1 แต่จริง ๆ แล้วเนี่ย ยังมีอีกเรื่องที่น้อง ๆ อาจจะสับสนเพราะชื่อคล้ายกันอยู่ นั่นก็คือ สมการกำลังสองตัวแปรเดียว นั่นเองงง ซึ่งวันนี้พี่ได้เตรียมทั้งสรุปเนื้อหา ตัวอย่างโจทย์พร้อมทั้งวิธีทำแบบละเอียดทั้งแบบที่ใช้สูตร และไม่ใช้สูตร มาให้ทุกคนด้วย ถ้าน้อง ๆ พร้อมแล้วไปทำความรู้จักสมการกำลังสองตัวแปรเดียวกันเลย !!

สนใจหัวข้อไหน ... กดอ่านเลย

สมการกำลังสองตัวแปรเดียว

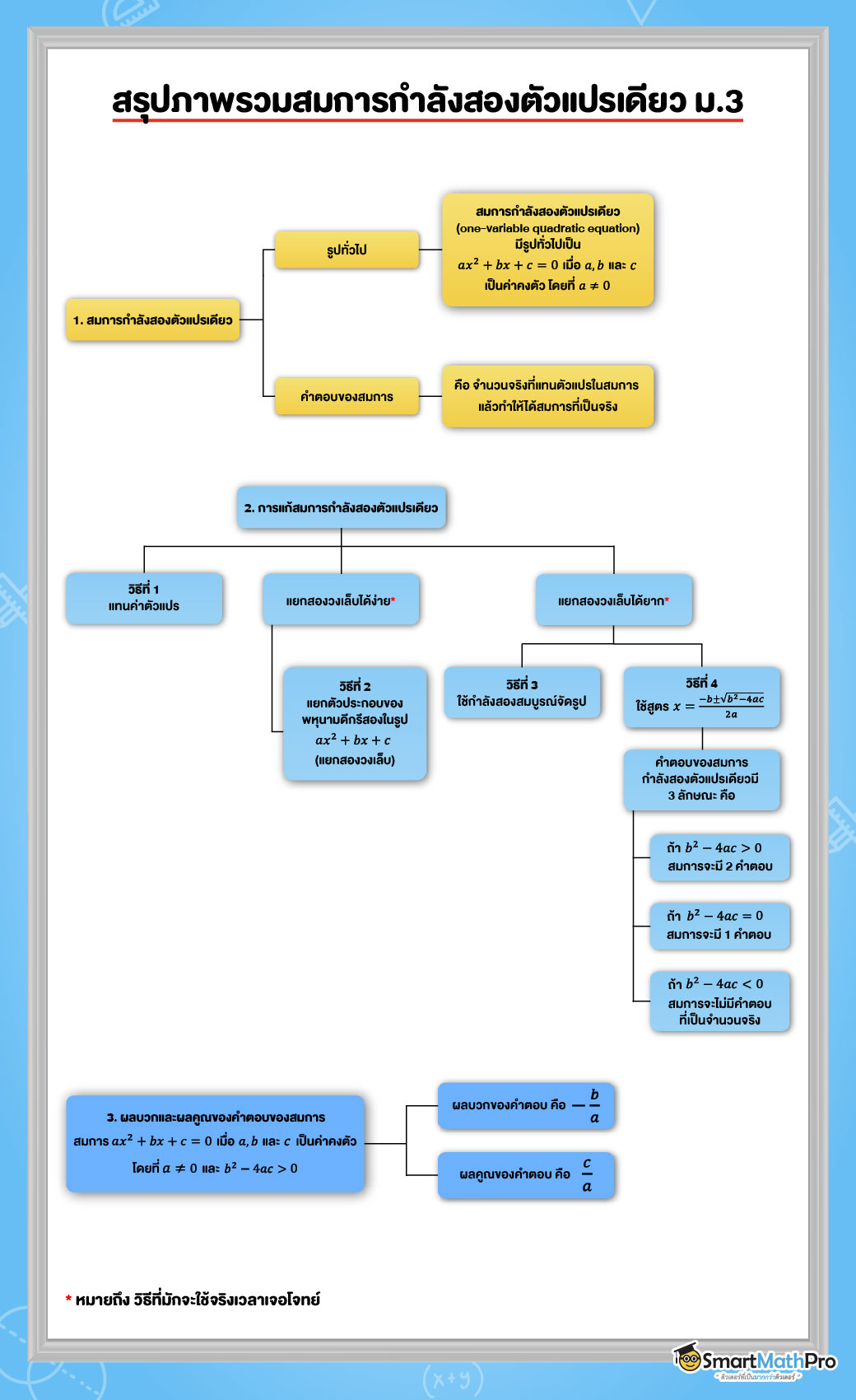
สมการกำลังสองตัวแปรเดียว คืออะไร ?

น้อง ๆ เคยรู้จักพหุนาม เช่น $3x^2 ,\ 2x^2+x,\ x^2-5$ และ $3x^2-6x+1$ ซึ่งเป็นพหุนามดีกรีสองมาแล้ว ในหัวข้อนี้เราจะมาเรียนเรื่องที่มีชื่อบทคล้ายกันนั่นคือสมการกำลังสองตัวแปรเดียว ซึ่งเป็นการนำพหุนามดีกรีสองมาใช้ต่อยอดนั่นเอง

เรามาพิจารณากันก่อนดีกว่า ว่าสมการแบบไหนนะ ที่เป็นสมการกำลังสองตัวแปรเดียว และสมการไหนที่ไม่เป็นสมการกำลังสองตัวแปรเดียว

จากรูปข้างต้น น้อง ๆ จะสังเกตได้ว่าสมการกำลังสองตัวแปรเดียวจะต้องมีลักษณะที่เมื่อจัดรูปแล้วมีรูปทั่วไปเป็นดังนี้

สมการกำลังสองตัวแปรเดียว คือ สมการของพหุนามตัวแปรเดียวที่มีดีกรีเท่ากับ 2 มีรูปทั่วไปเป็น
$ax^2+bx+c=0$ เมื่อ $x$ เป็นตัวแปร $a, b$ และ $c$ เป็นค่าคงตัว โดยที่ $a\neq 0$

หรือข้อสังเกตที่ดูได้ง่ายที่สุดเลยคือ สมการนั้นต้องมีตัวแปรเดียว ไม่ว่าจะเป็น $x, y$ หรือ $z$ ก็ได้นะ แต่ย้ำว่าต้องมีตัวแปรเดียว และต้องเป็นพหุนามที่มีดีกรีสอง ถ้าเป็นตามนี้แล้วไม่ว่าสัมประสิทธิ์นำจะเป็นบวก ลบ หรือเศษส่วนก็จะถือว่าเป็นสมการกำลังสองตัวแปรเดียวทั้งหมดเลยนะ

ก่อนที่จะไปแก้สมการกัน เราจะนิยมเขียนสมการที่โจทย์ให้มาให้อยู่ในรูปทั่วไปก่อน เพื่อให้เราแก้สมการได้ง่ายขึ้น ดังนั้นเรามาซ้อมเขียนสมการกำลังสองตัวแปรเดียวในรูปทั่วไปในตัวอย่างต่อไปนี้กันเลยดีกว่า

คำตอบของสมการกำลังสองตัวแปรเดียว

คำตอบของสมการ คือ จำนวนจริงที่เรานำไปแทนตัวแปรในสมการแล้วทำให้ได้สมการที่เป็นจริง ซึ่งคำตอบของสมการกำลังสองตัวแปรเดียวดังตัวอย่างต่อไปนี้

จากตัวอย่างข้างต้น น้อง ๆ บางคนอาจจะลองแทนค่าจำนวนจริงอื่น ๆ นอกจาก $x=0$ ลงในสมการ $x^2-x=0$ แล้วทำให้ได้สมการที่เป็นจริงอีกใช่ไหม นั่นแสดงว่าจำนวนคำตอบของสมการกำลังสองตัวแปรเดียวอาจไม่ได้มีเพียงคำตอบเดียวก็ได้ โดยน้อง ๆ ลองสังเกตตัวอย่างต่อไปนี้

น้อง ๆ จะสังเกตเห็นว่าในตัวอย่างแรก สมการ $x^2-x=0$ มีจำนวนจริงสองจำนวน ที่เมื่อนำไปแทนแล้วทำให้สมการเป็นจริง ดังนั้นสมการนี้จะมีจำนวนจริงสองจำนวนเป็นคำตอบ

ตัวอย่างถัดมา $y^2-4y+4=0$ มีจำนวนจริงเพียงจำนวนเดียวเป็นคำตอบ และ $x^2+4=0$ ไม่มีจำนวนจริงใดเป็นคำตอบเลย ในตัวอย่างนี้น้อง ๆ บางคนอาจจะจัดรูปสมการให้เป็น $x^2=-4$ ก่อนได้ แล้วจะพบว่าไม่มีจำนวนจริงไหนเลยที่เมื่อเรานำไปยกกำลังสองแล้วจะมีค่าเป็นจำนวนลบ

ดังนั้นสมการกำลังสองตัวแปรเดียวอาจมี 2 คำตอบ, 1 คำตอบ หรือไม่มีคำตอบที่เป็นจำนวนจริงเลยก็ได้ โดยในทางคณิตศาสตร์สมการกำลังสองตัวแปรเดียวมีคำตอบได้ไม่เกิน 2 คำตอบ

วิธีการแก้สมการกำลังสองตัวแปรเดียว

ความเป็นจริงพี่ไม่แนะนำให้น้อง ๆ ใช้วิธีการค่อย ๆ หาจำนวนจริงเพื่อนำไปแทนในสมการทีละตัวเพื่อตรวจสอบว่าจำนวนจริงนั้นทำให้สมการเป็นจริงหรือเท็จ เนื่องจากต้องใช้เวลามากและไม่สะดวก อาจจะหาจำนวนจริงที่เป็นคำตอบได้ไม่ครบหรืออาจหาไม่เจอ เช่น คำตอบเป็นจำนวนลบ เป็นเศษส่วน หรืออาจจะเป็นจำนวนอตรรกยะ !!!

ดังนั้นในการแก้สมการกำลังสองตัวแปรเดียวในบทนี้จะกล่าวถึงวิธีการที่สะดวกกว่าการแทนค่าทีละจำนวนไว้ 2 วิธี ได้แก่ การแยกตัวประกอบ และ การใช้สูตร โดยวิธีแรกจะเป็นวิธีที่เราจะได้ใช้ความรู้เรื่องการแยกตัวประกอบของพหุนามที่เคยเรียนมาช่วยแก้สมการได้อย่างที่พี่บอกตอนแรกน้าา

ถึงตรงนี้น้อง ๆ คนไหนที่ยังแยกตัวประกอบของพหุนามไม่คล่อง สามารถไปดูบทความที่พี่สรุปไว้ให้ได้เลย มีทั้งคำอธิบาย ตัวอย่าง แถมแจกแบบฝึดหัดให้ฟรีอีกด้วยยย

การแก้สมการกำลังสองตัวแปรเดียวโดยใช้การแยกตัวประกอบ

ในกรณีที่เราสามารถแยกตัวประกอบของ $ax^2+bx+c$ ให้อยู่ในรูปของการคูณกันสองพหุนามของพหุนามดีกรีหนึ่ง (แยกเป็นสองวงเล็บ) เนื่องจากในที่นี้พหุนามใช้แทนจำนวน เราจะใช้สมบัติของจำนวนจริงต่อไปนี้มาใช้ในการหาคำตอบของสมการ

สมบัติของจำนวนจริง
ถ้า $m$ และ $n$ เป็นจำนวนจริง และ $mn=0$ แล้ว $m=0$ หรือ $n=0$

นั่นคือหากพหุนามทั้งสองคูณกันแล้วมีค่าเท่ากับศูนย์ เราจะได้ว่าจะต้องมีพหุนามใดพหุนามหนึ่ง หรือทั้งสองพหุนามที่มีค่าเท่ากับศูนย์

เช่น

$(x)(x+1)=0$
มีพหุนามสองพหุนามคูณกัน คือ $x$ คูณกับ $x+1$ เมื่อสองพหุนามนั้นคูณกันแล้วได้ศูนย์
ดังนั้น ต้องมีพหุนามใดพหุนามหนึ่ง หรือทั้งสองพหุนามมีค่าเท่ากับศูนย์
จะได้ $x=0$ หรือ $x+1=0$

ถึงตรงนี้น้อง ๆ พอจะมองออกไหมว่าเราสามารถใช้การแยกตัวประกอบและสมบัติของจำนวนจริงมาแก้สมการได้อย่างไร จะเห็นว่าเราได้ $x=0$ ซึ่งเราจะได้คำตอบหนึ่งของสมการออกมาแล้วคือ 0 และส่วนที่เป็น $x+1=0$ เราจะต้องดำเนินการอีกเล็กน้อยก็จะได้คำตอบแล้ว พี่จะขอยกตัวอย่างการแก้สมการโดยใช้การแยกตัวประกอบแบบเต็ม ๆ ในตัวอย่างต่อไปนี้เลย

จากการตรวจคำตอบข้างต้น น้อง ๆ จะเห็นว่าเมื่อเรานำคำตอบที่ได้จากการแก้สมการด้วยวิธีการแยกตัวประกอบมาแทนลงในสมการ จะทำให้สมการเป็นจริง นั่นคือคำตอบที่เราหามาถูกต้องนั่นเองง

การแก้สมการโดยการใช้การแยกตัวประกอบสามารถนำมาใช้กับการแก้โจทย์ปัญหาเกี่ยวกับสมการกำลังสองตัวแปรเดียวได้เช่นกัน โดยน้อง ๆ จะต้องนำข้อมูลที่โจทย์กำหนดมาสร้างสมการกำลังสองตัวแปรเดียวให้ได้ จากนั้นเราก็จะทำการแก้สมการก็จะสามารถหาคำตอบได้แล้ว โดยลองกำหนดสิ่งที่โจทย์ต้องการให้หาเป็น $x$ ก็จะง่ายขึ้น ดังตัวอย่าง
ต่อไปนี้

(ต่อจากตัวอย่างที่ 3) เนื่องจาก $x$ แทนจำนวนเต็ม ดังนั้น $x$ จึงเป็นได้ทั้งจำนวนเต็มลบและจำนวนเต็มบวก

กรณีที่ 1
จำนวนที่มากกว่ามีค่าเท่ากับ -15
จะได้ว่า อีกจำนวนหนึ่งมีค่าเท่ากับ -16
กรณีที่ 2
จำนวนที่มากกว่ามีค่าเท่ากับ 16
จะได้ว่า อีกจำนวนหนึ่งมีค่าเท่ากับ 15

ตรวจสอบคำตอบกับเงื่อนไขของโจทย์

1) ผลคูณของ -15 และ -16 คือ (-15)(-16)=240

2) ผลคูณของ 15 และ 16 คือ (15)(16)=240

ดังนั้น จำนวนเต็มทั้งสองนั้นมี 2 ชุด คือ -15, -16 และ 15, 16

การแก้สมการกำลังสองตัวแปรเดียวโดยใช้สูตร

จากวิธีการแก้สมการโดยใช้การแยกตัวประกอบ อาจมีบางสมการที่ไม่สะดวกที่จะใช้วิธีแยกตัวประกอบ
เช่น $x^2-5x+5$ ดังนั้นน้อง ๆ สามารถใช้สูตรต่อไปนี้ในการช่วยแก้สมการได้

ตัวอย่างต่อไปนี้จะแสดงให้เห็นว่า หาก $b^2-4ac\geq 0$ จะได้ว่าสมการกำลังสองตัวแปรเดียวนั้นจะมี 2 คำตอบที่เป็นจำนวนจริง

ตัวอย่างต่อไปนี้จะแสดงให้เห็นว่า หาก $b^2-4ac=0$ จะได้ว่าสมการกำลังสองตัวแปรเดียวนั้นจะมีคำตอบที่เป็นจำนวนจริงเพียงคำตอบเดียว

ตัวอย่างต่อไปนี้จะแสดงให้เห็นว่า หาก $b^2-4ac<0$ จะได้ว่าสมการกำลังสองตัวแปรเดียวนั้นจะไม่มีคำตอบที่เป็นจำนวนจริง

เพื่อเป็นการประหยัดเวลาในการทำข้อสอบ ไม่โดนข้อสอบช็อตฟีลว่าแทนค่าลงในสูตรมาตั้งนาน สูตรก็ค่อนข้างยาว
แต่สมการไม่มีคำตอบเป็นจำนวนจริง

เราอาจตรวจสอบว่าสมการที่กำลังจะแก้นั้นมีคำตอบเป็นจำนวนจริงหรือไม่ก่อนก็ได้นะ ด้วยการแทนค่า $a, b$ และ $c$ ลงใน $b^2-4ac$ ก่อนที่จะแทนค่าในสูตรเต็ม เช่นในตัวอย่างก่อนหน้าคือตัวอย่างที่ 4 – 6 พี่จะตรวจสอบเฉพาะ $b^2-4ac$
มีค่ามากกว่าหรือเท่ากับศูนย์หรือไม่ แล้วจึงจะหาคำตอบของสมการต่อไป

น้อง ๆ ที่อ่านมาจนถึงตรงนี้ พี่เชื่อว่าคงจะเห็นภาพรวมของสมการกำลังสองตัวแปรเดียวกันแล้ว แต่แค่อ่านอย่างเดียวอาจจะยังไม่พอน้า ควรฝึกทำโจทย์เยอะ ๆ เพื่อให้เกิดความคุ้นชินด้วย สามารถดาวน์โหลดแบบฝึกหัด สมการกำลังสองตัวแปรเดียว ม.3 มาฝึกทำกันได้เลย และถ้าใครมีข้อสงสัย หรืออยากเข้าใจเนื้อหาให้ละเอียดขึ้น พี่แนะนำให้ไปดูคลิปติวเรื่องสมการกำลังสองตัวแปรเดียวเพิ่มเติมก็ได้น้าา

ติวคณิตศาสตร์ ม.ต้น กับ SmartMathPro

สำหรับน้อง ๆ ม.3 ที่ต้องการเก็บเกรดวิชาคณิตศาสตร์ให้ปัง ๆ แต่เคยลองทบทวนเนื้อหาด้วยตัวเองแล้ว ยังเจอจุดที่ไม่เข้าใจและอยากให้มีคนช่วยไกด์

พี่ขอแนะนำตัวช่วยอย่าง คอร์สคณิต ม.3 สอนโดยพี่ปั้น SmartMathPro ให้เลยย โดยแพ็กนี้จะสอนเนื้อหาทุกบททั้งเทอม 1 และเทอม 2 สอนสนุก เข้าใจง่าย (ใครพื้นฐานไม่ดีก็เรียนได้สบายมากก > <) พร้อมพาตะลุยโจทย์และมีแบบฝึกหัดให้แบบจัดเต็ม ไต่ระดับตั้งแต่แนวซ้อมมือ ข้อสอบในโรงเรียน และข้อสอบแข่งขัน ถ้าใครสนใจดูรายละเอียดเพิ่มเติม คลิก