
มีใครพอจะคุ้น ๆ กับชื่อบทเรียนในวิชาคณิตศาสตร์ อย่างเรื่อง ความน่าจะเป็น บ้างมั้ยน้าาา พี่เชื่อว่าน้อง ๆ หลายคนพอเห็นเรื่องนี้แล้วต้องสงสัยแน่ ๆ เลยว่าทำไมเรื่องที่เคยเรียนตอน ม.ต้น ถึงได้กลับมาเรียนอีกครั้งในคณิตม.ปลาย วันนี้พี่จะพาทุกคนไปหาคำตอบผ่านสรุปเนื้อหาเรื่องความน่าจะเป็น ม.5 ไปดูกันดีกว่าว่าสำหรับคณิตม.ปลาย บทนี้จะเรียนอะไร ยากกว่าม.ต้นมั้ย แถมพี่ยังมีตัวอย่างโจทย์ให้ทุกคนไว้ลองทำด้วยน้าา > <
สนใจหัวข้อไหน ... กดอ่านเลย
Toggleการนับและความน่าจะเป็น ม.5
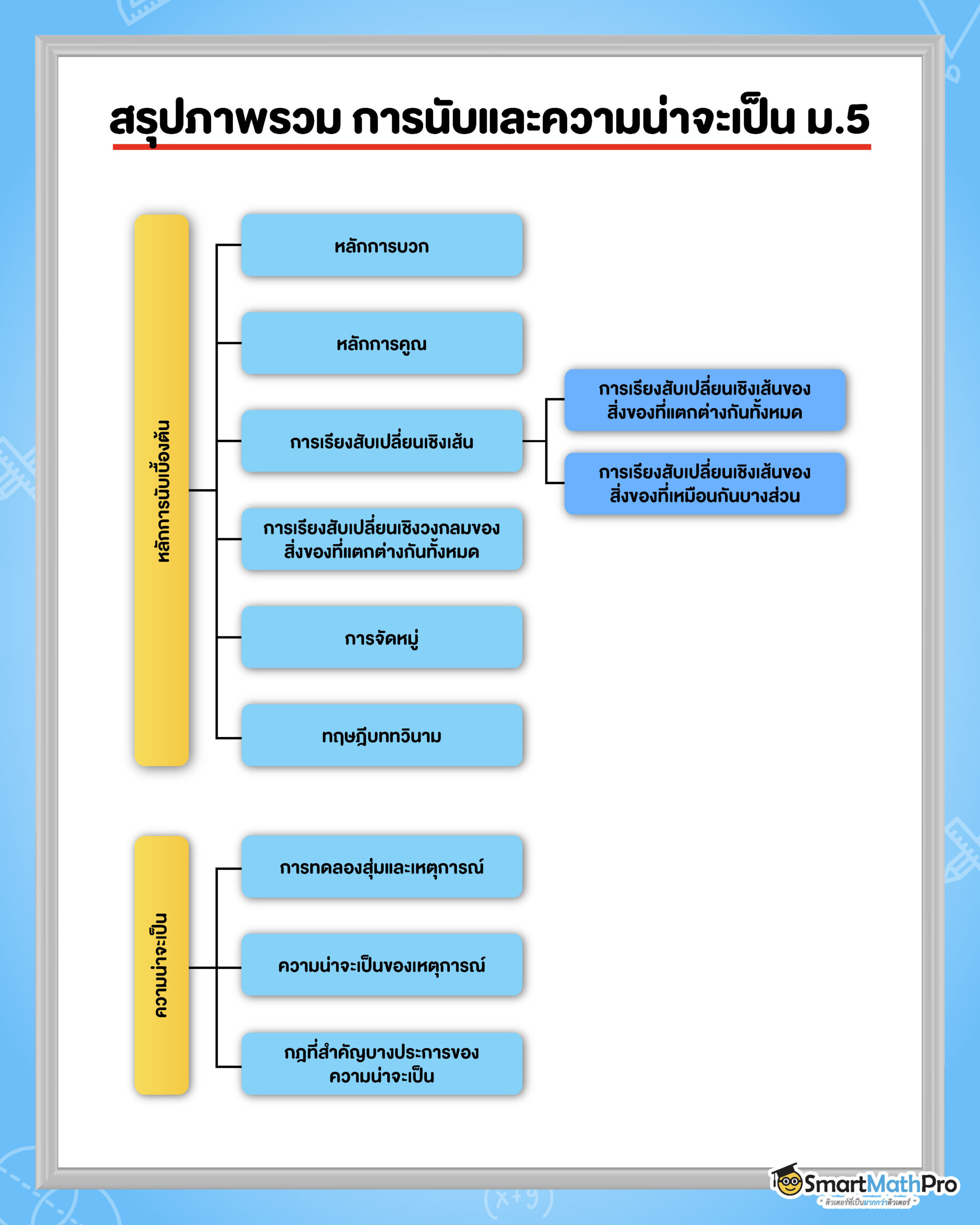
หลักการนับเบื้องต้น
น้อง ๆ เคยสงสัยไหม ว่าหัวข้อ หลักการนับเบื้องต้น จะกล่าวถึงการนับอะไร หมายถึงการนับจำนวนรึเปล่าา คำตอบก็คือหัวข้อนี้จะนับทุกอย่างเลยที่เราสนใจไม่ว่าจะเป็นสิ่งของ วิธีการหรือจำนวนก็ตาม แต่เราจะไม่นับอย่างสะเปะสะปะ เราจะนับแบบผู้มีหลักการมากขึ้น ซึ่งหลักการที่ว่าจะมีอะไรบ้าง เราไปดูพร้อมกันเลย !!
หลักการบวกและหลักการคูณ
หลักการบวก
ถ้าสามารถแบ่งวิธีการทำงานหนึ่งออกเป็น k กรณี ทำได้กรณีละ n_{k} วิธี และการทำงานในแต่ละกรณีทำให้งานเสร็จสมบูรณ์ แล้วจะสามารถทำงานนี้ได้ทั้งหมด n_{1}+n_{2}+n_{3}+ \cdots +n_{k} วิธี
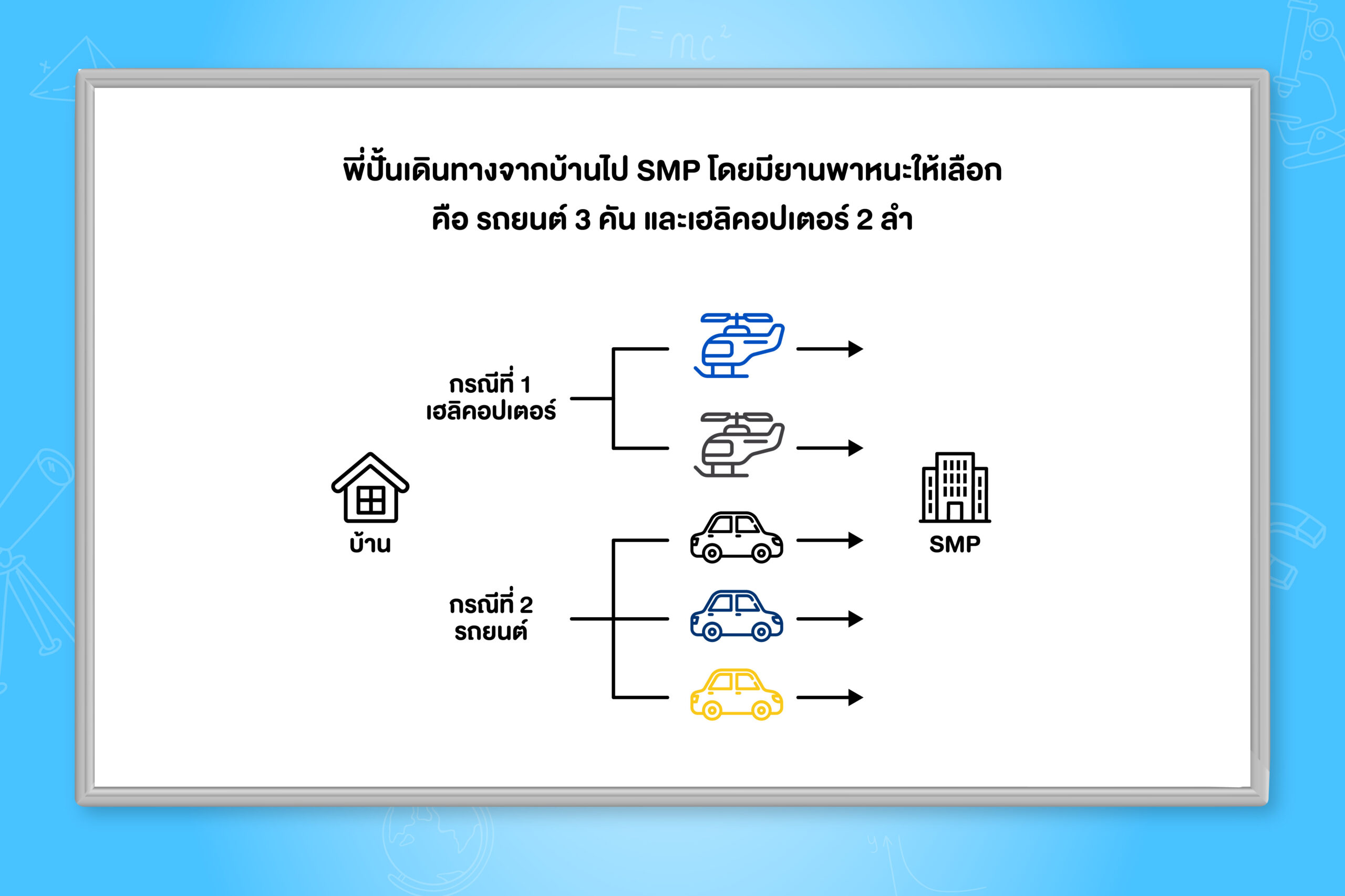
เช่น ถ้าพี่ปั้นต้องการเดินทางจากบ้าน ไปที่ SMP โดยมียานพาหนะ คือ รถยนต์ 3 คัน และเฮลิคอปเตอร์ 2 ลำ
พี่ปั้นสามารถเดินทางไปที่ SMP โดยใช้พาหนะอย่างเดียว ได้ 3+2=5 วิธี
หลักการคูณ
ถ้าสามารถแบ่งขั้นตอนการทำงานออกเป็น k ขั้นตอน ทำได้ขั้นตอนละ n_{k} วิธี
ซึ่งต้องทำต่อเนื่องกันแล้วจะสามารถทำงานนี้ได้ทั้งหมด n_{1}\times n_{2}\times n_{3}\times \cdots \times n_{k} วิธี
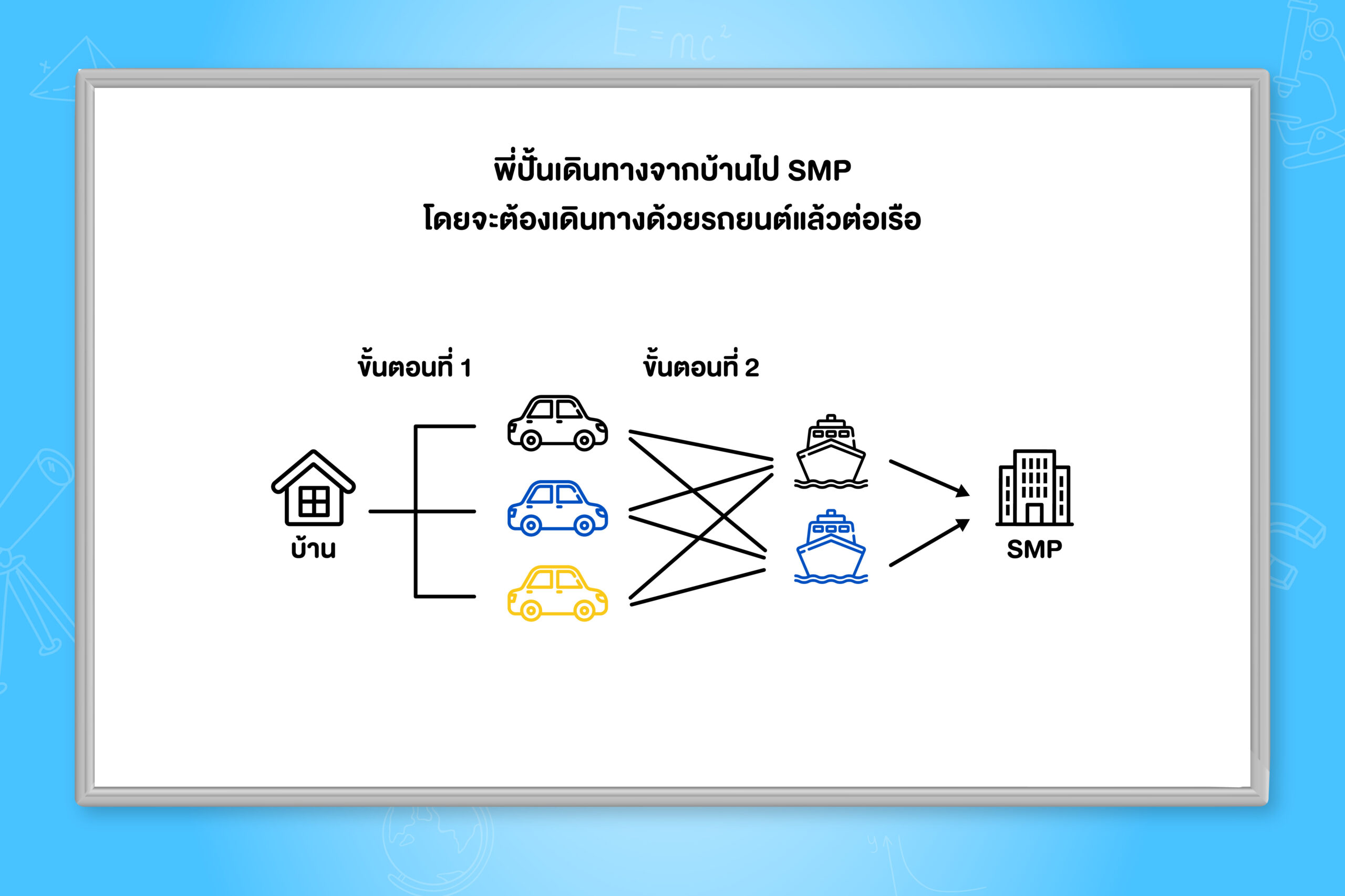
เช่น พี่ปั้นต้องการเดินทางจากบ้าน ไปที่ SMP โดยต้องเดินทางด้วยรถยนต์ แล้วต่อด้วยทางเรือ ถ้าพี่ปั้นมีรถยนต์ 3 คัน และเรือ 2 ลำ พี่ปั้นสามารถเดินทางไปที่ SMP โดยใช้ทั้งรถยนต์และเรือ ได้ 3\times 2=6 วิธี
พี่มีข้อสังเกตง่าย ๆ ว่าโจทย์ลักษณะไหนควรใช้หลักการบวกหรือหลักการคูณ ถ้าแต่ละวิธีทำให้งานเสร็จสมบูรณ์ เป็นการแบ่งกรณี จะต้องใช้หลักการบวก แต่ถ้างานที่ต้องทำต้องแบ่งขั้นตอนที่ต่อเนื่องกันงานถึงจะเสร็จสมบูรณ์จะต้องใช้หลักการคูณนั่นเอง
การเรียงสับเปลี่ยนเชิงเส้น
ในหัวข้อนี้เราจะมาเรียงสิ่งของต่าง ๆ กัน โดยมีเงื่อนไขคือจะเรียงเป็นเส้นตรงเท่านั้นน้า ยกตัวอย่างเหตุการณ์ที่น้อง ๆ สามารถเจอได้บ่อย ๆ เช่น การเข้าแถวหน้าชั้นเรียน โดยจะแบ่งการเรียงสับเปลี่ยนเชิงเส้นออกเป็น 2 แบบ คือการเรียงสับเปลี่ยนเชิงเส้นของสิ่งของที่แตกต่างกันทั้งหมด และการเรียงสับเปลี่ยนเชิงเส้นของสิ่งของที่ไม่แตกต่างกันทั้งหมด (บางชิ้นเหมือนกัน) จะมีวิธีคิดอย่างไรบ้าง ไปอ่านต่อกันได้เลยย
สิ่งของแตกต่างกันทั้งหมด
มีของที่แตกต่างกัน n ชิ้น นำมาเรียงทั้งหมด n ชิ้น ได้ n! วิธี
เช่น มีหนังสือ 4 วิชาที่แตกต่างกัน วิชาละ 1 เล่ม ต้องการนำทั้ง 4 เล่มมาเรียงกันเป็นเส้นตรง ได้
4!=4 \times 3 \times 2 \times 1=24 วิธี
มีของที่แตกต่างกัน n ชิ้น เลือกมาเรียง r ชิ้น ได้ P_{n,r}=\frac{n!}{(n-r)!} วิธี
ตัวอย่างที่ 1 พ่อ แม่ พี่ชาย พี่สาวและน้องหญิง นั่งเรียงกันเพื่อถ่ายรูป จะสามารถเรียงกันได้กี่วิธี ถ้าต้องการให้พ่อและแม่ไม่นั่งติดกัน
วิธีทำ
พี่ชาย พี่สาวและน้องหญิง สามารถนั่งตรงไหนก็ได้ แสดงว่าเลือกที่นั่งได้ 3! วิธี
พ่อและแม่ ต้องเลือกที่นั่งที่เป็นที่ว่างระหว่างแต่ละคน (มี 2 ที่นั่ง) หัวแถวหรือท้ายแถวรวมกัน มีทั้งหมด 4 ช่องว่าง
ให้พ่อและแม่นั่ง แสดงว่าเลือกที่นั่งได้ P_{4,2} วิธี
ทั้ง 5 คนสามารถนั่งได้ 3!\times P_{4,2} วิธี
จาก 3!= 3\times 2\times 1 =6
และ P_{4,2}=\frac{4!}{\left (4-2 \right )!}=\frac{4!}{2!}=4\times 3=12
ดังนั้น ทั้ง 5 คนสามารถนั่งได้ทั้งหมด 6\times 12=72 วิธี
สิ่งของไม่แตกต่างกันทั้งหมด
ถ้ามีสิ่งของ n ชิ้น ซึ่งมี n_{k} ชิ้นที่เหมือนกันในกลุ่มที่ k โดยที่ n_{1}+n_{2}+\cdots+n_{k}=n แล้วจำนวนวิธีเรียงสับเปลี่ยน เท่ากับ \frac{n!}{\left ( n_{1} \right )!\times \left ( n_{2} \right )!\times …\times \left ( n_{k} \right )!} วิธี
เช่น นำตัวอักษร A, A, B, B, B มาเรียงเป็นเส้นตรง
จะได้ว่ามีตัวอักษรทั้งหมด 5 ตัว แต่มี A ซ้ำกัน 2 ตัว และ B ซ้ำกัน 3 ตัว
จะได้ \frac{5!}{2!3!}=10 วิธี
การเรียงสับเปลี่ยนเชิงวงกลม
นอกจากการเรียงสับเปลี่ยนเชิงเส้นมาแล้วเราจะเรียงสับเปลี่ยนสิ่งของเชิงวงกลมได้ด้วย การนำสิ่งของชุดเดียวกันมาเรียงสับเปลี่ยนเชิงเส้นและเชิงวงกลมจะมีจำนวนวิธีที่แตกต่างกันด้วย พี่จะขอเปรียบเทียบให้ดูในแผนภาพต่อไปนี้น้า
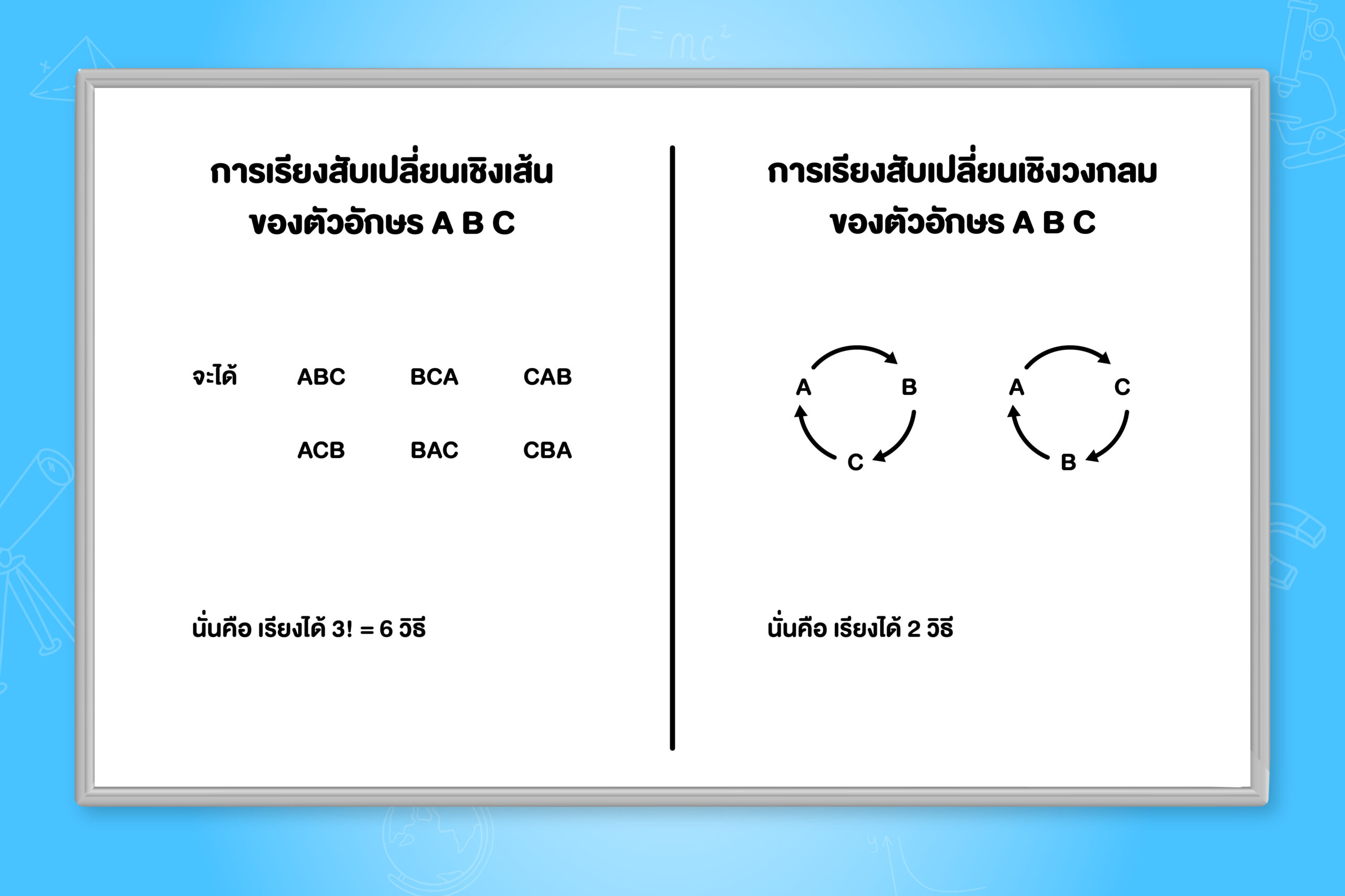
จำนวนวิธีในการเรียงสับเปลี่ยนเชิงวงกลมของสิ่งของที่แตกต่างกัน n ชิ้น เท่ากับ (n-1)! วิธี
ตัวอย่างที่ 2 นำรูปปั้นที่แตกต่างกันจำนวน 20 ตัว มาเรียงเป็นวงกลมเพื่อตกแต่งสวน ซึ่งรูปปั้นทั้งหมดจะมีรูปปั้นหมาและแมวอย่างละ 1 ตัว ถ้าต้องการจัดให้รูปปั้นหมาและแมวอยู่ติดกัน จะวางรูปปั้นได้ทั้งหมดกี่แบบ
วิธีทำ
ต้องการจัดวางให้รูปปั้นหมาและแมวอยู่ติดกัน จะถือว่ารูปปั้นหมาและแมวรวมกันเสมือนเป็นรูปปั้นตัวเดียวกัน
ดังนั้น จะเสมือนมีรูปปั้นทั้งหมด 19 ตัว ซึ่งเรียงเป็นวงกลมได้ (19-1)!=18! แบบ
เนื่องจาก สามารถสลับที่รูปปั้นหมาและแมวได้ 2 แบบ
ดังนั้น จะจัดรูปปั้นทั้งหมดเป็นวงกลมโดยที่รูปปั้นหมาและแมวอยู่ติดกันได้ 18!\times 2 แบบ
การจัดหมู่ของสิ่งของที่แตกต่างกันทั้งหมด
ถ้าน้อง ๆ กำลังสงสัยว่าการเรียงสับเปลี่ยนกับการจัดหมู่มีความแตกต่างกันอย่างไร ให้ลองคิดตามพี่น้า
ถ้าพี่มีลูกอมอยู่ในกล่องทั้งหมด 3 เม็ด โดยมีลูกอมสีเขียว (G) สีแดง (R) และสีม่วง (P) อย่างละหนึ่งเม็ด ให้น้อง ๆ พิจารณาการหยิบต่อไปนี้
- หยิบลูกอม 2 เม็ด โดยหยิบทีละเม็ดและไม่ใส่คืน
จะได้ GR, GP, RG, RP, PG, PR นั่นคือได้ 6 วิธี
น้องจะเห็นว่า GR RG ถือเป็นวิธีที่แตกต่างกัน เพราะการหยิบสิ่งของทีละ 1 ชิ้นและไม่ใส่คืน เราจะ “สนใจลำดับ” ในการหยิบด้วย - หยิบลูกอม 2 เม็ด ครั้งหนึ่ง โดยหยิบพร้อมกัน
จะได้ GR, GP, RP นั่นคือได้ 3 วิธี
น้องจะเห็นว่า พี่ไม่สลับ GR กับ RG แล้ว เพราะการหยิบลูกอมขึ้นมาพร้อมกัน เราจะ “ไม่สนใจลำดับ” ในการหยิบ จะถือว่าการหยิบลูกอมได้สีเขียวและสีแดง หรือหยิบได้สีแดงและสีเขียว เป็นวิธีเดียวกัน
ถ้าน้อง ๆ เข้าใจความแตกต่างของการเรียงสับเปลี่ยนและการจัดหมู่แล้ว มาดูสูตรต่อไปนี้พร้อมกันเลย
จำนวนวิธีจัดหมู่ของสิ่งของที่แตกต่างกันทั้งหมด n ชิ้น โดยเลือกคราวละ r ชิ้น คือ
C_{n, r}=\binom{n}{r}=\frac{n!}{(n-r)!r!} วิธี
ตัวอย่างที่ 3 เจริญมีหนังสือทั้งหมด 10 เล่ม พรต้องการยืมหนังสือจากเจริญไปอ่าน 3 เล่ม จงหาว่าพรจะยืมหนังสือจากเจริญได้ทั้งหมดกี่วิธี
วิธีทำ
ต้องการเลือกหนังสือ 3 เล่ม จากหนังสือทั้งหมด 10 เล่ม ทำได้ C_{10, 3}
จะได้ว่า C_{10, 3}=\frac{10!}{(10-3)!3!}=\frac{10!}{7!3!}=\frac{10\times 9\times 8}{3\times 2\times 1}=120
ดังนั้น จะเลือกยืมหนังสือ 3 เล่ม จากทั้งหมด 10 เล่ม ได้ 120 วิธี
ทฤษฎีบททวินาม
ให้น้อง ๆ ลองมาพิจารณาการสร้างพหุนามต่อไปนี้ เมื่อ x, y เป็นจำนวนจริงใด ๆ
(x+y)^2
= (x+y)(x+y)
=x^2+2xy+y^2
(x+y)^3 = (x+y)(x+y)(x+y) =(x^2+2xy+y^2)(x+y) =x^3+3x^2y+3xy^2+y^3
จะสังเกตเห็นว่าการกระจาย (x+y)^n เมื่อ n เป็นจำนวนเต็มบวก ทำได้โดยเลือก x หรือ y อย่างใดอย่างหนึ่งของแต่ละวงเล็บมาคูณกัน แล้วนำผลลัพธ์ที่ได้มาบวกกัน
เช่น จาก (x+y)^3 ให้เลือก y จาก 2 วงเล็บใด ๆ มาคูณกัน และเลือก x จาก 1 วงเล็บที่เหลือมา จะได้พจน์ จาก xy^2 ซึ่งจะมีทั้งหมด 3 พจน์ จึงได้เป็น 3xy^2 และทำในทำนองเดียวกันจนครบรูปแบบ เราก็จะได้การกระจาย (x+y)^n ตามที่เราต้องการ
การกระจาย (x+y)^n สามารถสรุปเป็นทฤษฎีบทได้ดังนี้

ถ้าน้อง ๆ ต้องการพิจารณาเพียงบางพจน์จากการกระจาย (x+y)^n สามารถใช้สูตรด้านล่างนี้ได้เลยย
พจน์ที่ r+1 จากการกระจาย (x+y)^n จะมีค่าเท่ากับ T_{r+1}=\binom{n}{r}x^{n-r}y^r
ตัวอย่างที่ 4 จงหาสัมประสิทธิ์ของ x^4y^5 ในการกระจาย (2x+3y)^9
วิธีทำ
จากทฤษฎีบททวินาม พจน์ที่มี x^4y^5 คือ
\binom{9}{5}(2x)^4(3y)^5=\frac{9!}{4!5!}\cdot 2^43^5x^4y^5=(126) 2^43^5x^4y^5
ดังนั้น สัมประสิทธิ์ของ x^4y^5 คือ (126)2^43^5
ความน่าจะเป็น
ก่อนเราจะเข้าเนื้อหาเกี่ยวกับความน่าจะเป็น พี่ขอพาน้อง ๆ มาทำความรู้จักกับคำสำคัญที่ควรรู้กันก่อนน้าา
คำสำคัญ
การทดลองสุ่ม (Random experiment)
การทดลองซึ่งทราบว่าผลลัพธ์อาจจะเป็นอะไรได้บ้าง แต่บอกอย่างแน่นอนไม่ได้ว่า ในแต่ละครั้งที่ทดลองผลที่เกิดขึ้นจะเป็นอะไร
ปริภูมิตัวอย่าง (Sample space)
เซตที่มีสมาชิกเป็นผลลัพธ์ที่อาจจะเป็นไปได้ทั้งหมดของการทดลองสุ่ม
เหตุการณ์ (Event)
เซตที่มีสมาชิกเป็นผลลัพธ์ที่เราสนใจจากการทดลองสุ่มซึ่งเป็นสับเซตของปริภูมิตัวอย่าง
ตอนนี้น้อง ๆ ได้รู้จักคำสำคัญของเรื่องความน่าจะเป็นแล้ว มารู้จักบทนิยามของความน่าจะเป็นกันต่อดีกว่า
ความหมายของความน่าจะเป็น
ความน่าจะเป็น หมายถึงจำนวนที่บ่งบอกถึงโอกาสที่เหตุการณ์นั้น ๆ จะเกิดขึ้นซึ่งมีบทนิยามทางคณิตศาสตร์ดังนี้
บทนิยาม
ให้ S แทนปริภูมิตัวอย่างซึ่งเป็นเซตจำกัด โดยที่สมาชิกทุกตัวของ S มีโอกาสเกิดขึ้นเท่ากัน และให้ E แทนเหตุการณ์ที่เป็นสับเซตของ S
ความน่าจะเป็นของเหตุการณ์ E เขียนแทนด้วย P(E) นิยามโดย
P(E)= \frac{n(E)}{n(S)}
เมื่อ n(E) แทนจำนวนสมาชิกของเหตุการณ์ E
และ n(S) แทนจำนวนสมาชิกของปริภูมิตัวอย่าง S
P(E)=0 หมายความว่า เหตุการณ์ E ไม่มีโอกาสเกิดขึ้น
P(E)=1 หมายความว่า เหตุการณ์ E จะเกิดขึ้นอย่างแน่นอน
ตัวอย่างที่ 5 เด็กชายปั้นปูนสุ่มหยิบสลาก 2 ใบจากกล่องที่บรรจุสลากหมายเลข 1 – 5 อย่างละ 1 ใบ จงหาความน่าจะเป็นที่หยิบสลากได้หมายเลขที่เป็นจำนวนคี่ทั้ง 2 ใบ
วิธีทำ
n(S) คือ จำนวนสมาชิกของเหตุการณ์ที่หยิบสลาก 2 ใบจากสลาก 5 ใบ
n(S)=\binom{5}{2}=10
เหตุการณ์หยิบสลากได้จำนวนคี่ทั้ง 2 ใบ เนื่องจากหมายเลขที่เป็นจำนวนคี่มี 3 ตัว ได้แก่ หมายเลข 1, 3, 5 เลือกหยิบมา 2 ใบ
n(E)=\binom{3}{2}=3
ดังนั้น ความน่าจะเป็นที่หยิบสลากได้จำนวนคี่ทั้ง 2 ใบเท่ากับ P(E)=\frac{n(E)}{n(S)}=\frac{3}{10}
ตัวอย่างที่ 6 มีลูกบอลสีเขียว 5 ลูก และมีลูกบอลสีแดง 4 ลูก จงหาความน่าจะเป็นที่จะหยิบลูกบอลขึ้นมา 3 ลูกแล้วได้ลูกบอกสีเขียวอย่างน้อย 1 ลูก
วิธีทำ
ปริภูมิตัวอย่าง คือ จำนวนสมาชิกของเหตุการณ์ที่หยิบลูกบอล 3 ลูกจากลูกบอลทั้งหมด 9 ลูก
n(S)=\binom{9}{3}=\frac{9!}{6!3!}= 84
เหตุการณ์หยิบลูกบอลสีเขียวอย่างน้อย 1 ลูก
แนวคิด : ถ้าคิดด้วยวิธีตรงตัวเราต้องคิดกรณีที่หยิบลูกบอลสีเขียวได้ 1 ลูก, หยิบลูกบอลสีเขียวได้ 2 ลูก, และหยิบลูกบอลสีเขียวได้ 3 ลูก ดังนั้นพี่จึงแนะนำให้น้องใช้เทคนิคนำจำนวนสมาชิกของปริภูมิตัวอย่างลบด้วยเหตุการณ์ตรงข้าม ({E}') ดีกว่า
เหตุการณ์หยิบไม่ได้ลูกบอลสีเขียวเลย นั่นคือ จากลูกบอลสีแดง 4 ลูกหยิบมา 3 ลูก
จะได้ว่า n({E}')=\binom{4}{3}= 4
เหตุการณ์หยิบลูกบอลสีเขียวอย่างน้อย 1 ลูก
จะได้ว่า n(E) = n(S) – n({E}')=84–4=80
ดังนั้น ความน่าจะเป็นที่จะหยิบลูกบอลขึ้นมา 3 ลูกแล้วได้ลูกบอกสีเขียวอย่างน้อย 1 ลูก เท่ากับ
P(E)=\frac{n(E)}{n(S)}=\frac{80}{84}= \frac{20}{21}
พื้นฐานของความน่าจะเป็น
- ให้ S แทนปริภูมิตัวอย่างซึ่งเป็นเซตจำกัด สำหรับเหตุการณ์ E ใด ๆ จะได้ว่า 0\le P(E)\le1
- ความน่าจะเป็นของปริภูมิตัวอย่าง S เท่ากับ 1 หรือ P(S)=1
- ความน่าจะเป็นของเหตุการณ์ที่เป็นเซตว่างหรือเหตุการณ์ที่เป็นไปไม่ได้ เท่ากับ 0 หรือ P(\emptyset)=0
กฎที่สำคัญบางประการของความน่าจะเป็น
ให้ S เป็นปริภูมิตัวอย่างซึ่งเป็นเซตจำกัด และ A, B เป็นเหตุการณ์ใด ๆ จะได้ว่า
- ความน่าจะเป็นของเหตุการณ์ A หรือ เหตุการณ์ B คือ P(A\cup B)
ความน่าจะเป็นของเหตุการณ์ A และ เหตุการณ์ B คือ P(A\cap B)
โดยมีความสัมพันธ์ดังนี้
P(A\cup B)=P(A)+P(B)-P(A\cap B) - เมื่อ A\cap B= \varnothing แสดงว่าเหตุการณ์ A และเหตุการณ์ B ไม่เกิดร่วมกัน (mutually exclusive events) จะได้ว่า P(A\cap B)=0 และ P(A\cup B)=P(A)+P(B)
- ความน่าจะเป็นของเหตุการณ์ที่ประกอบด้วยสมาชิกที่อยู่ในปริภูมิตัวอย่าง แต่ไม่อยู่ในเหตุการณ์นั้น คือ
P(A^\prime)=1-P(A) - ความน่าจะเป็นของเหตุการณ์ที่ประกอบด้วยสมาชิกที่อยู่ใน A แต่ไม่อยู่ในเหตุการณ์ B คือ
P(A-B)=P(A)-P(A\cap B)
ติวคณิตศาสตร์ ม.ปลาย กับ SmartMathPro
เนื้อหาคณิตศาสตร์ ม.ปลาย อาจดูเป็นเรื่องยากในความคิดของน้อง ๆ หลายคน แต่ที่จริงถ้าเรามีพื้นฐานที่ดี ทบทวนบทเรียนและฝึกทำโจทย์บ่อย ๆ ก็จะทำให้เข้าใจในเนื้อหามากขึ้น แต่ถ้าใครยังกังวล กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากได้คนช่วยไกด์
พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
ข้อสอบคณิตพร้อมเฉลย
ดูคลิปติวคณิต ม.5 เทอม 1 และ 2
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
สมบัติบางประการของความน่าจะเป็นจะมีลักษณะคล้าย ๆ กับสมบัติในเรื่องเซตเลย ถ้าจำสมบัติในเรื่องเซตได้ การจำสมบัติความน่าจะเป็นนี้ไปใช้ไม่ใช่เรื่องยากเลยน้าา ดังนั้นการมีพื้นฐานแน่น ๆ ถึงได้สำคัญมาก เพราะน้อง ๆ สามารถต่อยอดได้หลายบทเลย แต่ใครที่รู้สึกว่าพื้นฐานไม่แน่น หรือยังไม่มั่นใจ พี่แนะนำให้ลองโหลดโจทย์และแบบฝึกหัดมาลองทำดูน้า การฝึกทำโจทย์เยอะ ๆ จะช่วยทบทวนเนื้อหาไปในตัวด้วยย
บทความ แนะนำ
บทความ แนะนำ

ทีมวิชาการคณิตศาสตร์
ผู้อยู่เบื้องหลังการจัดทำคอร์สเรียนร่วมกับพี่ติวเตอร์
และผู้เขียนบทความวิชาการคณิตศาสตร์ของสถาบัน SmartMathPro

ทีมวิชาการคณิตศาสตร์
ผู้อยู่เบื้องหลังการจัดทำคอร์สเรียนร่วมกับพี่ติวเตอร์
และผู้เขียนบทความวิชาการคณิตศาสตร์ของสถาบัน SmartMathPro
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro





















