มีน้อง ๆ ม.6 คนไหนอยากได้สรุปเนื้อหาคณิตศาสตร์ ม.ปลาย อยู่บ้างงง สำหรับบทที่พี่เอามาฝากทุกคนวันนี้คือ
บทตัวแปรสุ่มและการแจกแจงความน่าจะเป็น ม.6 นั่นเองง
โดยพี่ได้สรุปหัวข้อสำคัญ ๆ มาให้ทุกคนตั้งแต่ การแจกแจงความน่าจะเป็นของตัวแปรสุ่มไม่ต่อเนื่อง (ค่าคาดหมาย,
การแจกแจงทวินาม) และการแจกแจงความน่าจะเป็นของตัวแปรสุ่มต่อเนื่อง (การแจกแจงปกติมาตรฐาน และการแจกแจงปกติ) จะมีเนื้อหาอย่างไรบ้าง ไปดูกันเล้ยยย
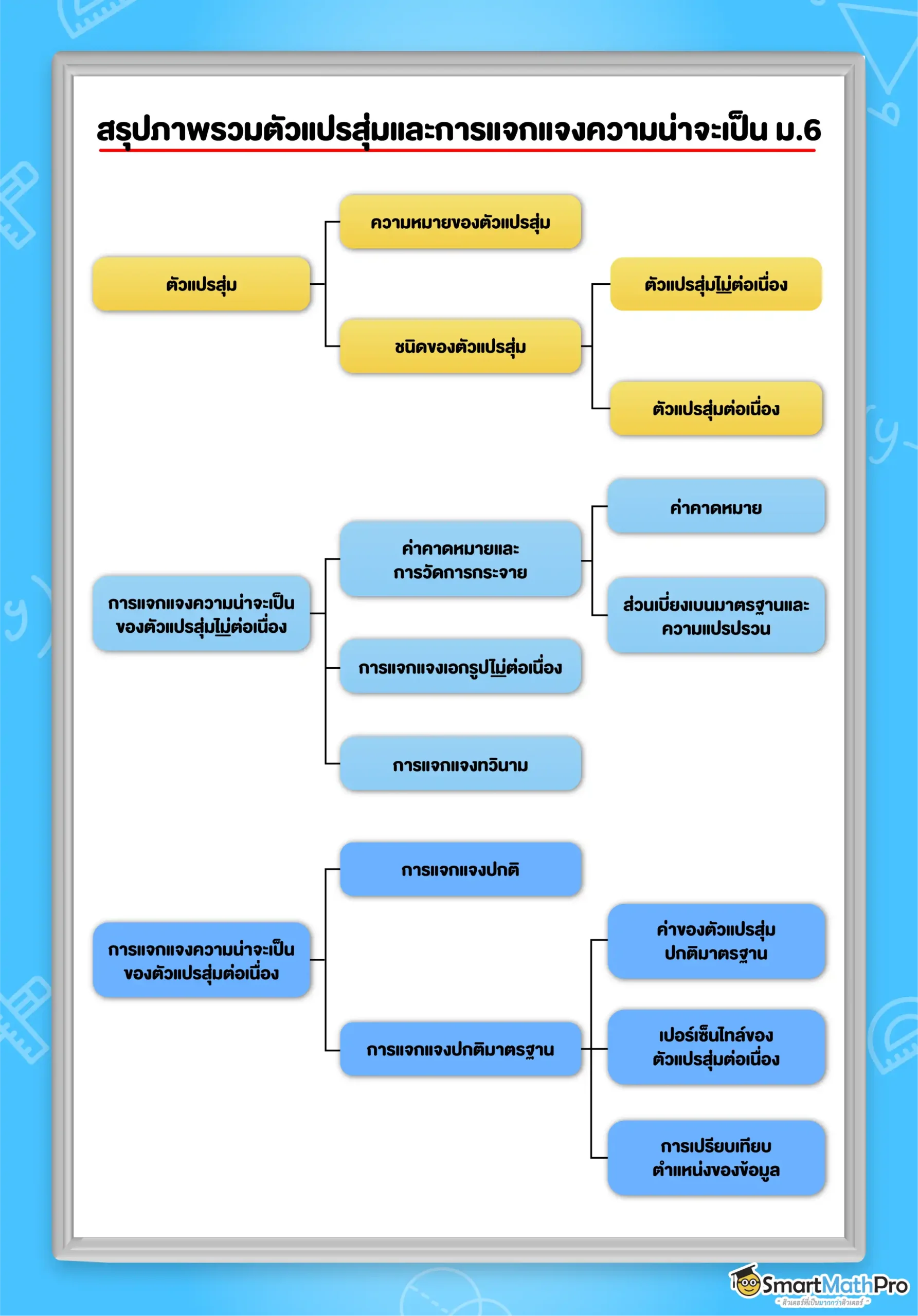
ตัวแปรสุ่ม
ความหมายของตัวแปรสุ่ม
เราลองมาโยนเหรียญที่เที่ยงตรง 1 เหรียญ 2 ครั้งกัน โดย H แทนเหรียญขึ้นหัว และ T แทนเหรียญขึ้นก้อย จะได้ปริภูมิตัวอย่างของการทดลองสุ่มนี้ คือ \left\{TT, HT, TH, HH\right\} ซึ่งถ้าเราลองมานับจำนวนครั้งที่เหรียญขึ้นหัว จากการโยนเหรียญจะได้ว่า
TT มีเหตุการณ์ที่เหรียญขึ้นหัว 0 ครั้ง
TH และ HT มีเหตุการณ์ที่เหรียญขึ้นหัว 1 ครั้ง
HH มีเหตุการณ์ที่เหรียญขึ้นหัว 2 ครั้ง
จากการทดลองสุ่มครั้งนี้ สิ่งที่เราสนใจ คือ จำนวนครั้งที่เหรียญขึ้นหัว ซึ่งเราจะเรียกสิ่งนี้ว่าตัวแปรสุ่ม และผลลัพธ์ที่ได้จากตัวแปรสุ่ม \left (0, 1, 2 \right) ครั้ง จะเรียกว่า ค่าของตัวแปรสุ่ม หรือ ค่าที่เป็นไปได้ของตัวแปรสุ่ม
บทนิยาม
ตัวแปรสุ่ม (random variable) คือ ฟังก์ชันจากปริภูมิตัวอย่างของการทดลองสุ่มไปยังเซตของจำนวนจริง
และเรียกสมาชิกของเรนจ์ของตัวแปรสุ่มว่า ค่าของตัวแปรสุ่ม มักจะใช้ X, Y, Z (ตัวอักษรพิมพ์ใหญ่) แทนตัวแปรสุ่ม ใช้ x, y, z (ตัวอักษรพิมพ์เล็ก) แทนค่าของตัวแปรสุ่ม และใช้ X=x แทนเหตุการณ์ที่ค่าของตัวแปรสุ่มเป็น x
ตัวอย่างที่ 1 กำหนดให้ตัวแปรสุ่ม X คือ จำนวนครั้งที่ลูกเต๋าขึ้นแต้ม 3 จากการโยนลูกเต๋า 1 ลูก 3 ครั้ง จงหาค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่ม X
แนวคิด
สามารถเกิดได้ทั้งหมด 4 กรณี
- กรณีที่ 1 โยนลูกเต๋า 3 ครั้ง ขึ้นแต้ม 3 ทั้งหมด 0 ครั้ง
แปลว่าไม่มีครั้งไหนขึ้นแต้ม 3 เลย (เช่น ทอดลูกเต๋าได้แต้ม 2, 1, 4 ตามลำดับ)
จะได้ว่า ค่าของตัวแปรสุ่ม X คือ 0 เขียนได้เป็น X=0 - กรณีที่ 2 โยนลูกเต๋า 3 ครั้ง ขึ้นแต้ม 3 ทั้งหมด 1 ครั้ง
แปลว่าอาจจะเป็นครั้งที่ 1, 2 หรือ 3 ก็ได้ แต่ขึ้นเพียงครั้งเดียว (เช่น ทอดลูกเต๋าได้แต้ม 3, 1, 4 ตามลำดับ)
จะได้ว่า ค่าของตัวแปรสุ่ม X คือ 1 เขียนได้เป็น X=1 - กรณีที่ 3 โยนลูกเต๋า 3 ครั้ง ขึ้นแต้ม 3 ทั้งหมด 2 ครั้ง
แปลว่าอาจจะเป็นครั้งที่ 1, 2 หรือ 3 ก็ได้ แต่ขึ้นรวมกันทั้งหมด 2 ครั้ง (เช่น ทอดลูกเต๋าได้แต้ม 3, 1, 3 ตามลำดับ)
จะได้ว่า ค่าของตัวแปรสุ่ม X คือ 2 เขียนได้เป็น X=2 - กรณีที่ 4 โยนลูกเต๋า 3 ครั้ง ขึ้นแต้ม 3 ทุกครั้ง (นั่นคือ ทอดลูกเต๋าได้แต้ม 3, 3, 3 ตามลำดับ)
จะได้ว่า ค่าของตัวแปรสุ่ม X คือ 3 เขียนได้เป็น X=3
ตอบ ค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่ม X คือ 0, 1, 2, 3
เราจะสามารถเขียนในรูปสัญลักษณ์ได้เป็น X=x โดยที่ x\in \left\{0, 1, 2, 3\right\}
ชนิดของตัวแปรสุ่ม
โดยทั่วไปตัวแปรสุ่มสามารถแบ่งได้เป็น 2 ชนิด ตามลักษณะของค่าที่เป็นไปได้ของตัวแปรสุ่ม ดังนี้
- ตัวแปรสุ่มไม่ต่อเนื่อง (discrete random variable) คือ ตัวแปรสุ่มที่ค่าที่เป็นไปได้ทั้งหมดเขียนอยู่ในรูปเซต
ที่สามารถนับจำนวนสมาชิกได้ หรือสามารถเขียนเรียงลำดับจากน้อยไปมากได้ เช่น ตัวแปรสุ่ม
X_{1} คือ จำนวนพี่น้อง (คน) ทั้งหมด ของนักเรียนในห้อง - ตัวแปรสุ่มต่อเนื่อง (continuous random variable) คือ ตัวแปรสุ่มที่ค่าที่เป็นไปได้ทั้งหมด
เขียนอยู่ในรูปช่วงที่เป็นสับเซตของ \mathbb{R} เช่น ตัวแปรสุ่ม X_{2} คือ เวลา (วินาที) ที่นักกีฬาใช้ในการวิ่งรอบสนาม 400 เมตร
การแจกแจงความน่าจะเป็นของตัวแปรสุ่มไม่ต่อเนื่อง
การนําความน่าจะเป็นของการเกิดค่าแต่ละค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่ม มาแสดงในรูปตารางหรือกราฟ เพื่ออธิบายลักษณะของตัวแปรสุ่ม เรียกว่า การแจกแจงความน่าจะเป็น ดังตัวอย่างต่อไปนี้
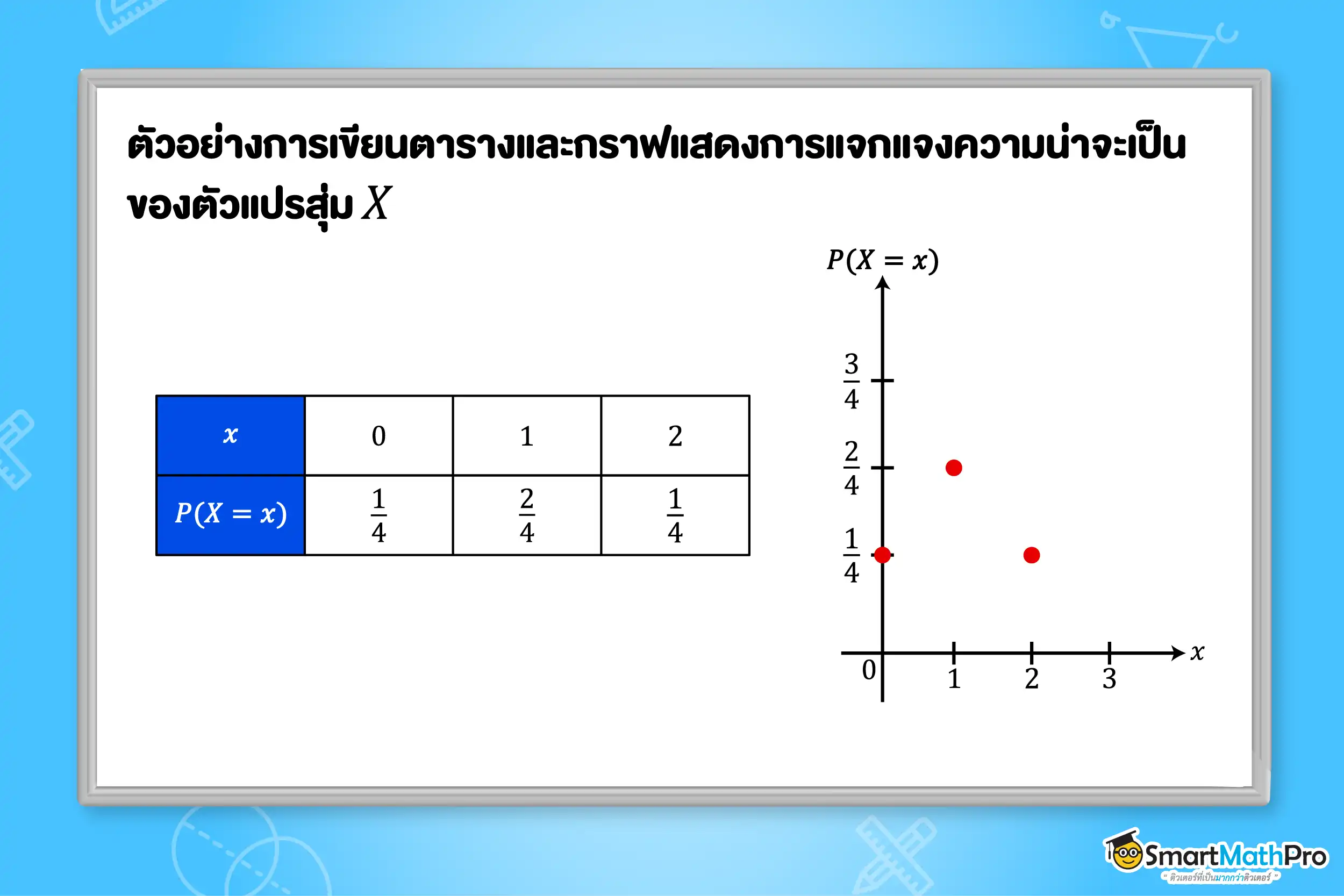
ตัวอย่างที่ 2 ให้ตัวแปรสุ่ม X คือ จำนวนครั้งที่เหรียญขึ้นหัว จากการที่หมีเนยโยนเหรียญเที่ยงตรง 1 เหรียญ 2 ครั้ง จงเขียนแสดงการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X ในรูปตารางและกราฟ
แนวคิด เราจะสร้างตารางโดยแบ่งเป็น จำนวนครั้งเหรียญที่ขึ้นหัว x ครั้ง และค่าของความน่าจะเป็น P(X=x)
ค่ากลางและการวัดการกระจาย
ค่าคาดหมายของตัวแปรสุ่มไม่ต่อเนื่อง
ตัวอย่างที่ 3 จำนวนเงินที่นักเรียน ม.6 ของโรงเรียน SMP จำนวน 20 คน นำมาโรงเรียน เป็นดังตารางความถี่
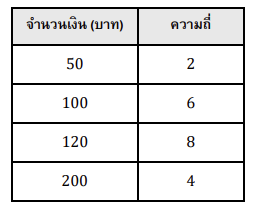
ถ้าสุ่มนักเรียน 1 คน จากห้องนี้ และให้ตัวแปรสุ่ม X คือ จำนวนเงิน (บาท) ของนักเรียนที่สุ่มได้ จงหาค่าคาดหมายของตัวแปรสุ่ม X
วิธีทำ
พิจารณาสิ่งที่โจทย์กำหนดให้
จาก \mu _{x}=\sum_{i=1}^{n}x_{i}\cdot P(X=x_{i})
\mu _{x}=x_{1}\cdot P(X=x_{1})+x_{2}\cdot P(X=x_{2})+x_{3}\cdot P(X=x_{3})+x_{4}\cdot P(X=x_{4})
จะได้ว่า \mu _{x}=(50)\left ( \frac{2}{20} \right )+(100)\left ( \frac{6}{20} \right )+(120)\left ( \frac{8}{20} \right )+(200)\left ( \frac{4}{20} \right )
\mu _{x}=5+30+48+40
\mu _{x}=123 บาท
ค่าคาดหมายของตัวแปรสุ่ม X คือ 123 บาท
ส่วนเบี่ยงเบนมาตรฐานของตัวแปรสุ่มไม่ต่อเนื่อง
น้อง ๆ รู้ไหมว่า นอกจากค่าคาดหมายแล้ว เราสามารถนิยามส่วนเบี่ยงเบนมาตรฐานของตัวแปรสุ่มเพื่อใช้ในการวัดการกระจายของค่าที่เป็นไปได้ของตัวแปรสุ่มว่ามีความแตกต่างจากค่าคาดหมายมากหรือน้อยเพียงใดได้ด้วย
ตัวอย่างที่ 4 สุ่มนักเรียนของพี่ลั่นปุ้นมา 1 คน จากทั้งหมด 5 คน ให้ตัวแปรสุ่ม X คือ จำนวนไก่แจ้ในบ้านของนักเรียนที่สุ่มได้ โดยข้อมูลของจำนวนไก่แจ้ของนักเรียนเป็นดังตารางต่อไปนี้
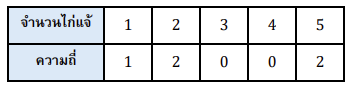
จงหาส่วนเบี่ยงเบนมาตรฐานและความแปรปรวน
แนวคิด เนื่องจากสูตรส่วนเบี่ยงเบนมาตรฐาน มีการนำค่า x แต่ละตัวลบออกด้วยค่าคาดหมาย ดังนั้นเราจะหาค่าคาดหมายของตัวแปรสุ่มก่อน เพื่อนำไปหาส่วนเบี่ยงเบนมาตรฐาน และเมื่อได้ส่วนเบี่ยงเบนมาตรฐานเราสามารถนำไปยกกำลังสอง เพื่อหาค่าความแปรปรวนต่อได้
วิธีทำ พิจารณาค่าคาดหมายของตัวแปรสุ่ม X
\mu _{x}=\sum_{i=1}^{n}x_{i}\cdot P(X=x_{i})
\mu _{x}=(1)\left ( \frac{1}{5} \right )+(2)\left ( \frac{2}{5} \right )+(3)\left ( \frac{0}{5} \right )+(4)\left ( \frac{0}{5} \right )+(5)\left ( \frac{2}{5} \right )
\mu _{x}=0.2+0.8+0+0+2
\mu _{x}=3
1. ส่วนเบี่ยงเบนมาตรฐานของตัวแปรสุ่ม X
\sigma _{x}=\sqrt[]{\sum_{i=1}^{n}(x_{i}-\mu _{x})^{2}\cdot P(X=x_{i})}
\sigma _{x}=\sqrt{(1-3)^{2}\cdot \left ( \frac{1}{5} \right )+(2-3)^{2}\cdot \left ( \frac{2}{5} \right )+(3-3)^{2}\cdot\left ( \frac{0}{5} \right )+(4-3)^{2}\cdot \left ( \frac{0}{5} \right )+(5-3)^{2}\cdot \left ( \frac{2}{5} \right ) }
\sigma _{x}=\sqrt{\left ( \frac{4}{5} \right )+\left ( \frac{2}{5} \right )+0+0+\left ( \frac{8}{5} \right ) }
\sigma _{x}=\sqrt{\frac{14}{5}}
2. ความแปรปรวนของตัวแปรสุ่ม X
จากส่วนเบี่ยงเบนมาตรฐานของตัวแปรสุ่ม \sigma _{x}=\sqrt[]{\frac{14}{5}}
จะได้ ความแปรปรวนของตัวแปรสุ่มเป็น \sigma_{x}^{2}=\frac{14}{5} หรือ \sigma_{x}^{2}=2.8 นั่นเอง
ส่วนเบี่ยงเบนมาตรฐานของตัวแปรสุ่ม X คือ \sqrt{\frac{14}{5}} และความแปรปรวนของตัวแปรสุ่ม X คือ \frac{14}{5}
การแจกแจงเอกรูปไม่ต่อเนื่อง
จากบทนิยาม เราสรุปได้ว่าค่าที่เป็นไปได้ของตัวแปรสุ่มแต่ละค่าจะต้องมีความน่าจะเป็นเท่ากันนั่นเอง
- การแจกแจงความน่าจะเป็นของตัวแปรสุ่มที่เป็นการแจกแจงเอกรูปไม่ต่อเนื่อง
เช่น ตัวแปรสุ่ม X คือ จำนวนครั้งที่เหรียญขึ้นก้อยจากการโยนเหรียญเที่ยงตรง 1 เหรียญ 1 ครั้ง จะได้ว่า P(X=x)=\frac{1}{2} โดยที่ x\in \left\{ 0, 1 \right\} - การแจกแจงความน่าจะเป็นของตัวแปรสุ่มที่ไม่เป็นการแจกแจงเอกรูปไม่ต่อเนื่อง
เช่น ตัวแปรสุ่ม X คือ จำนวนครั้งที่เหรียญขึ้นก้อย จากการโยนเหรียญเที่ยงตรง 1 เหรียญ 2 ครั้ง เนื่องจาก P(X=1)=\frac{2}{4} แต่ P(X=2)=\frac{1}{4} ดังนั้น P(X=1)\neq P(X=2)
การแจกแจงทวินาม
บทนิยาม
การแจกแจงทวินาม คือ การแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X ซึ่งคือจำนวนครั้งของการเกิดผลสำเร็จจากการทดลองสุ่ม n ครั้ง เป็นอิสระกัน โดยในแต่ละครั้งมีโอกาสเกิดผลสำเร็จด้วยความน่าจะเป็นเท่ากับ p และไม่เกิดผลสำเร็จด้วยความน่าจะเป็นเท่ากับ 1-p
จากบทนิยาม การแจกแจงทวินามคือตัวแปรสุ่มไม่ต่อเนื่องที่มีลักษณะดังนี้
- เป็นการทำการทดลองซ้ำ ๆ กัน โดยแต่ละครั้งจะเป็นอิสระต่อกัน
- ผลที่ได้จะมี 2 แบบเสมอ คือ สำเร็จหรือไม่สำเร็จ
- ในแต่ละครั้งของการทดลองสุ่ม ความน่าจะเป็นที่สำเร็จ คือ p และไม่สำเร็จคือ 1-p
และเราสามารถเขียนสัญลักษณ์ X\sim B(n,p) เพื่อแสดงว่าการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X เป็นการแจกแจงทวินามที่มี n และ p เป็นพารามิเตอร์ โดย
n หมายถึงจำนวนครั้งของการทดลองสุ่ม
p หมายถึงความน่าจะเป็นที่จะเกิดผลสำเร็จในการทดลองสุ่มแต่ละครั้ง
นอกจากจะเขียน P(X=x) แทนความน่าจะเป็นของเหตุการณ์ที่ค่าของตัวแปรสุ่ม X เป็น x แล้วยังสามารถเขียนในรูปของอสมการได้ เช่น P(X<x) แทน ความน่าจะเป็นของตัวแปรสุ่ม X ที่มีค่าน้อยกว่า x และ P(X\geq x) แทน ความน่าจะเป็นของตัวแปรสุ่ม X ที่มีค่ามากกว่าหรือเท่ากับ x
ตัวอย่างที่ 5 กำหนดให้ X\sim B(5,0.3) จงหา
1. P(x=2)
วิธีทำ
จาก X\sim B(5,0.3)
จะได้ว่า n=5 และ p=0.3 จากทฤษฎีบท P(X=x)=\binom{n}{x}p^{x}(1-p)^{n-x}
จะได้ว่า P(X=2)=\binom{5}{2}(0.3)^{2}(1-0.3)^{5-2}\approx 0.31
2. P(X<2)
วิธีทำ
P(X<2)
=P(X=0)+P(X=1)
=\binom{5}{0}(0.3)^{0}(1-0.3)^{5-0}+\binom{5}{1}(0.3)^{1}(1-0.3)^{5-1}
\approx 0.53
ตัวอย่างที่ 6 น้องปั้นเป่ายิงฉุบกับเพื่อน พบว่าโอกาสที่น้องปั้นจะเป่ายิงฉุบชนะในแต่ละครั้งคือ 0.4 ที่เหลือเป็นแพ้หมด (สมมติว่าหากเป่ายิงฉุบเสมอจะไม่นับ ต้องเป่ายิงฉุบใหม่) กำหนดให้ตัวแปรสุ่ม X คือ จำนวนครั้งที่น้องปั้นเป่ายิงฉุบชนะ หากน้องปั้นเป่ายิงฉุบทั้งหมด 6 ครั้ง จงหา
แนวคิด จากโจทย์ น้องปั้นเป่ายิงฉุบ 6 ครั้งและโอกาสที่จะชนะ 0.4 เราจะได้ว่า n=6 และ p=0.4 ดังนั้น 1-p=0.6
1. ความน่าจะเป็นที่น้องปั้นจะเป่ายิงฉุบชนะอย่างน้อย 1 ครั้ง
วิธีทำ
แสดงว่าโจทย์ต้องการหา P(X\geq 1)
จาก P(X\geq 1)=P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)+P(X=6)
น้องจะเห็นว่าเราต้องคำนวณเยอะมากเพื่อหาค่าของ P(X\geq 1)
แต่เราสามารถหา P(X\geq 1) จาก 1-P(x< 1)=1-P(x=0) ได้น้า
จะได้ว่า P(x\geq 1)=1-P(X=0)=1-\binom{6}{0}(0.4)^{0}(1-0.4)^{6-0}\approx 0.95
2. ค่าคาดหมายของการเป่ายิงฉุบและอธิบายความหมาย
วิธีทำ
จาก \mu _{x}=np=6(0.4)=2.4
หมายความว่าโดยเฉลี่ยแล้วจากการที่น้องปั้นเป่ายิงฉุบ 6 ครั้ง จะชนะ 2.4 ครั้ง
3. ส่วนเบี่ยงเบนมาตรฐานของการเป่ายิงฉุบและอธิบายความหมาย
วิธีทำ
จาก \sigma _{x}=\sqrt{np(1-p)}=\sqrt{6(0.4)(0.6)}=1.2
หมายความว่าในการเป่ายิงฉุบ 6 ครั้ง จำนวนครั้งที่จะชนะจะต่างจากค่าคาดหมาย 1.2 ครั้ง
การแจกแจงความน่าจะเป็นของตัวแปรสุ่มต่อเนื่อง
เรนจ์ของตัวแปรสุ่มต่อเนื่องเป็นช่วงที่เป็นสับเซตของจำนวนจริง ซึ่งมีสมาชิกเป็นจำนวนอนันต์ ดังนั้นกราฟของการแจกแจงความน่าจะเป็นของตัวแปรสุ่มต่อเนื่องจะมีลักษณะเป็นเส้นโค้ง เรียกว่า เส้นโค้งความหนาแน่น (density curve)
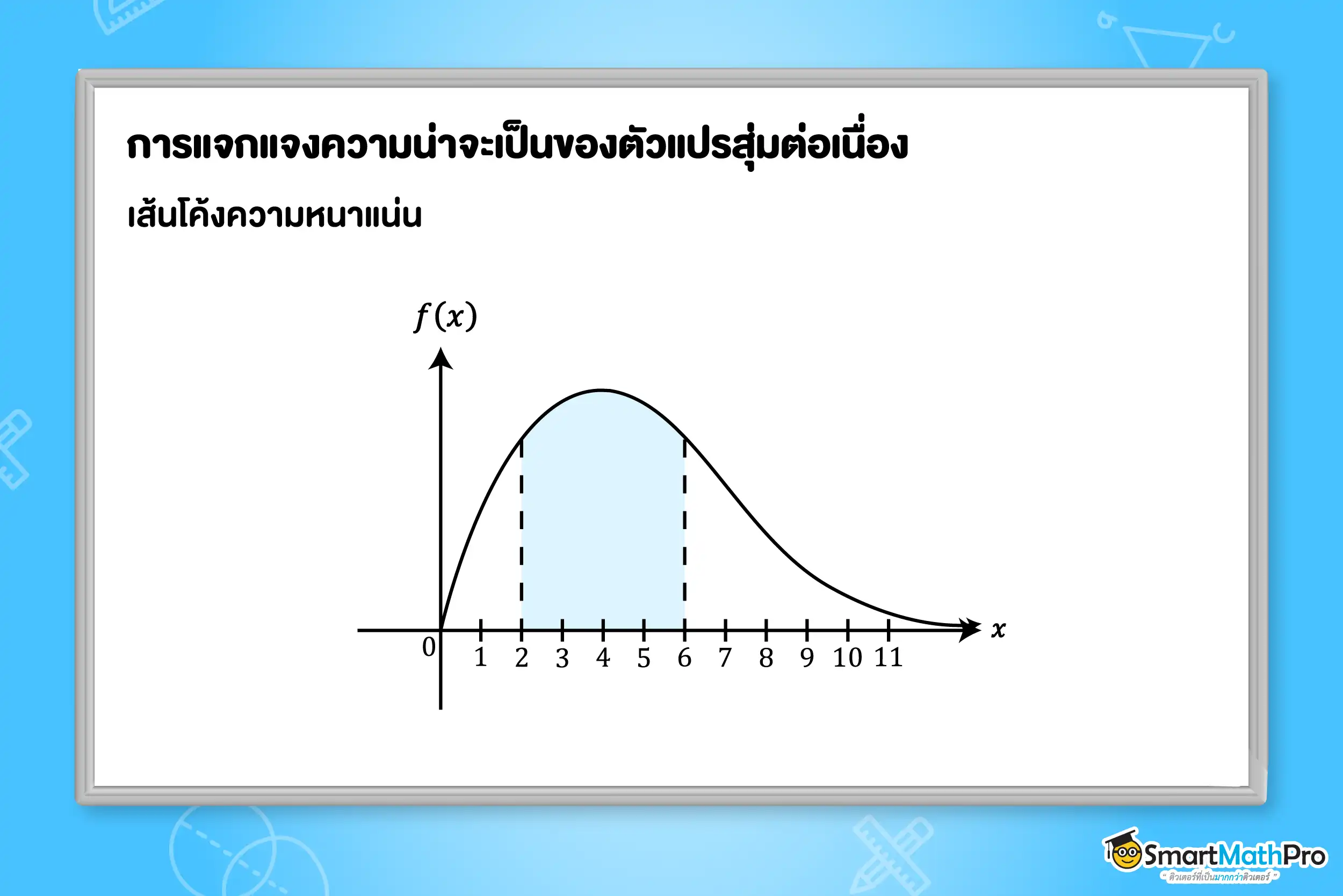
ฟังก์ชันความหนาแน่นความน่าจะเป็น (probability density function) คือ ฟังก์ชันของเส้นโค้งความหนาแน่นซึ่งเป็นกราฟของฟังก์ชัน y=f(x) โดยที่ x แทนค่าที่เป็นไปได้ของตัวแปรสุ่ม
พื้นที่ใต้เส้นโค้งความหนาแน่น คือ พื้นที่ที่ปิดล้อมด้วยเส้นโค้งความหนาแน่นกับแกน X ในช่วงนั้น จะเท่ากับความน่าจะเป็นที่ตัวแปรสุ่มจะมีค่าอยู่ในช่วงใดช่วงหนึ่ง
ข้อตกลงเกี่ยวกับเส้นโค้งความหนาแน่นที่ควรทราบ
- พื้นที่ใต้เส้นโค้งความหนาแน่นทั้งหมดจะเท่ากับ 1 เพราะ ผลรวมของความน่าจะเป็นทั้งหมด คือ 1 นั่นเอง
- P(X=x_{i})=0 เนื่องจากเป็นตัวแปรสุ่มต่อเนื่อง การหาความน่าจะเป็นจะดูเป็นช่วง ทำให้ ณ ตำแหน่งใดตำแหน่งหนึ่งความน่าจะเป็นจึงเท่ากับ 0
- P(X\leq x_{i})=P(X< x_{i}) และ P(X\geq x_{i})=P(X>x_{i}) เพราะ P(X=x_{i})=0
การแจกแจงปกติ
การแจกแจงปกติ (normal distribution) คือ การแจกแจงความน่าจะเป็นของตัวแปรสุ่มต่อเนื่อง X ที่มีฟังก์ชันความหนาแน่นความน่าจะเป็นบางฟังก์ชันกำกับอยู่ ซึ่งกราฟของฟังก์ชันหรือเส้นโค้งความหนาแน่น
มีลักษณะดังนี้
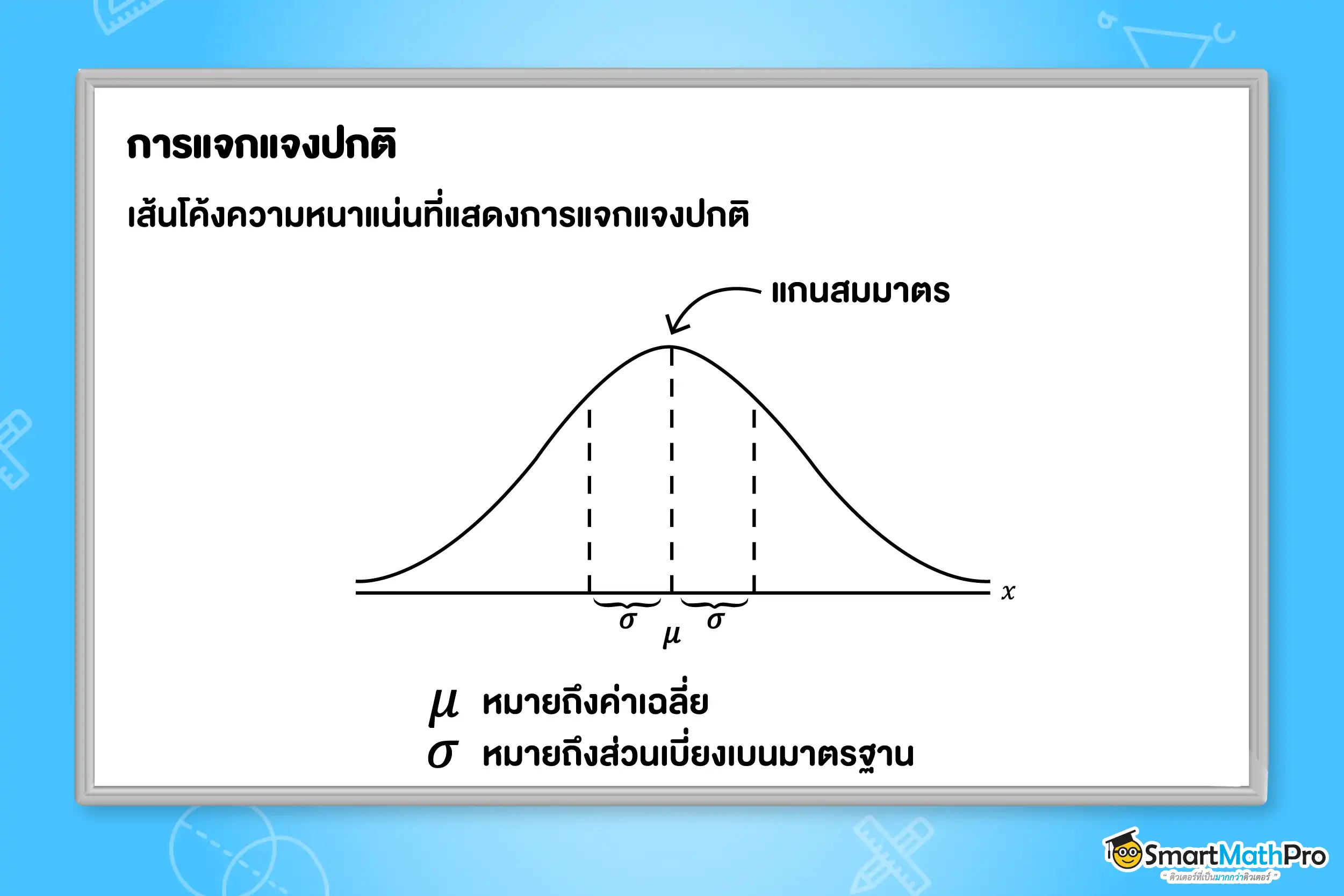
ค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของตัวแปรสุ่มจะเป็นตัวกำหนดลักษณะเฉพาะของเส้นโค้งว่าแกนสมมาตรอยู่ที่ใดบนเส้นจำนวนและมีค่าการกระจายจากค่าเฉลี่ยมากน้อยแค่ไหนนั่นเอง
เราจะเขียนสัญลักษณ์ X\sim N(\mu ,\sigma ^{2}) เพื่อแสดงว่าตัวแปรสุ่ม X มีการแจกแจงปกติ โดยที่ \mu และ \sigma ^{2} เป็นพารามิเตอร์
การแจกแจงปกติมาตรฐาน
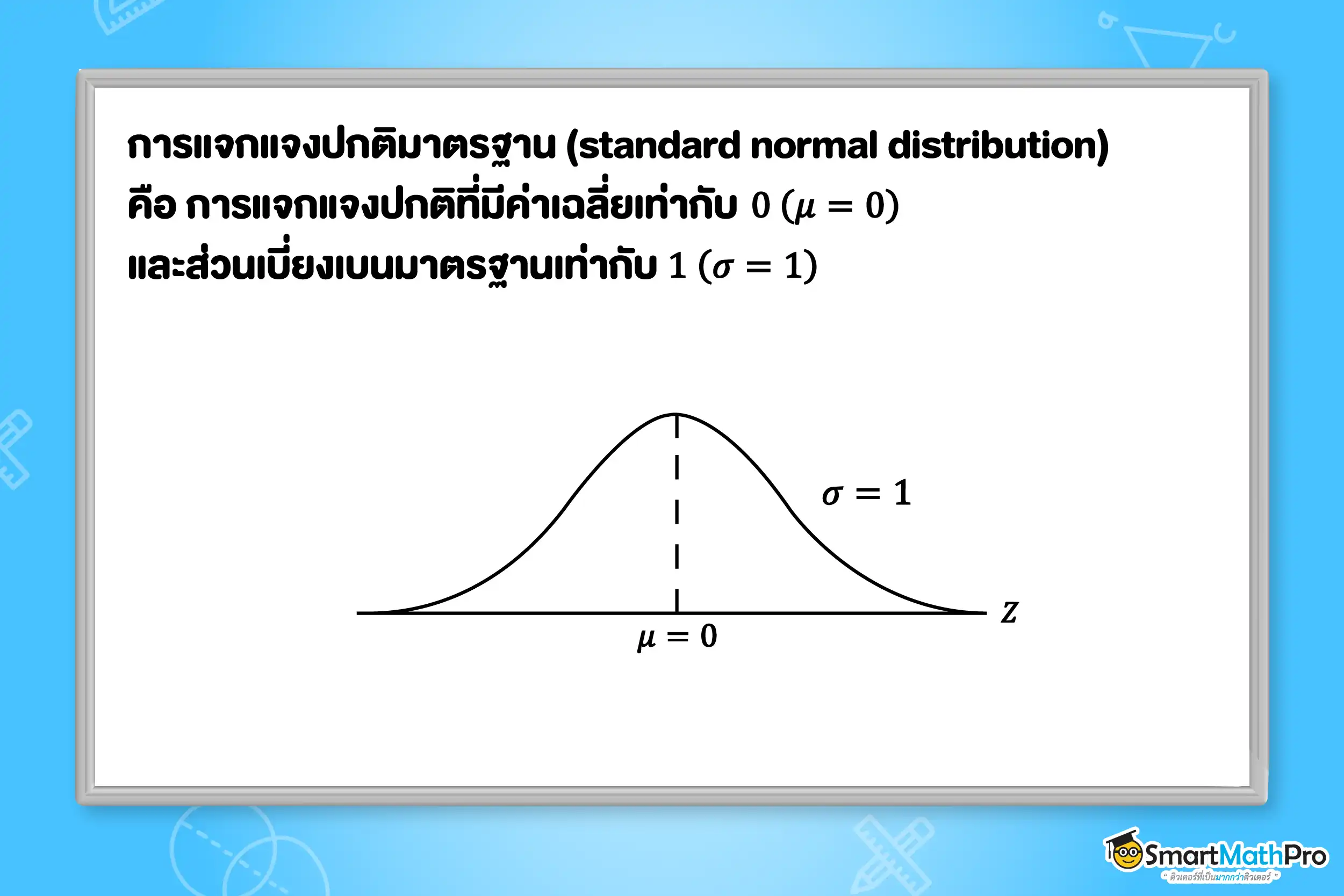
เส้นโค้งความหนาแน่นซึ่งได้จากตัวแปรสุ่มปกติ เรียกว่า เส้นโค้งปกติมาตรฐาน (standard normal curve) และเรียกตัวแปรสุ่ม Z ที่มีการแจกแจงปกติมาตรฐานว่า ตัวแปรสุ่มปกติมาตรฐาน (standard normal random variable)
ความน่าจะเป็นของตัวแปรสุ่มปกติมาตรฐาน
ความน่าจะเป็นของตัวแปรสุ่มปกติมาตรฐานจะมีค่าเท่ากับพื้นที่ใต้เส้นโค้งปกติตามช่วงที่เราพิจารณา ในหัวข้อตัวแปรสุ่มต่อเนื่องนี้ การหาพื้นที่ใต้เส้นโค้งความหนาแน่นต้องใช้ความรู้การหาปริพันธ์จำกัดเขตจากบทแคลคูลัส ซึ่งยากต่อการคำนวณเอง เราจึงใช้ตารางต่อไปนี้ในการหาพื้นที่ใต้เส้นโค้งของ Z แต่ละค่า เพื่อให้เข้าใจมากยิ่งขึ้น พี่จะพาน้อง ๆ ไปดูการอ่านตารางแสดงพื้นที่ใต้เส้นโค้งปกติมาตรฐานผ่านตัวอย่างต่อไปนี้กัน
ตัวอย่างที่ 7 ให้ Z เป็นตัวแปรสุ่มปกติมาตรฐาน และกำหนดตารางแสดงพื้นที่ใต้เส้นโค้งปกติมาตรฐาน ดังต่อไปนี้ จงหา P(Z\leq 0.45) และ P(-0.45\leq Z\leq 1.50)
แนวคิด การอ่านค่าตารางแสดงพื้นที่ใต้เส้นโค้งปกติมาตรฐานที่ P(Z\le a) จะมีพื้นที่เท่ากับค่าในตารางได้เลย ถ้าต้องการหา P ที่อยู่ระหว่างค่า z 2 ค่า ให้นำพื้นที่ที่ค่า z มากกว่าตั้ง แล้วลบด้วยค่า z ที่น้อยกว่า
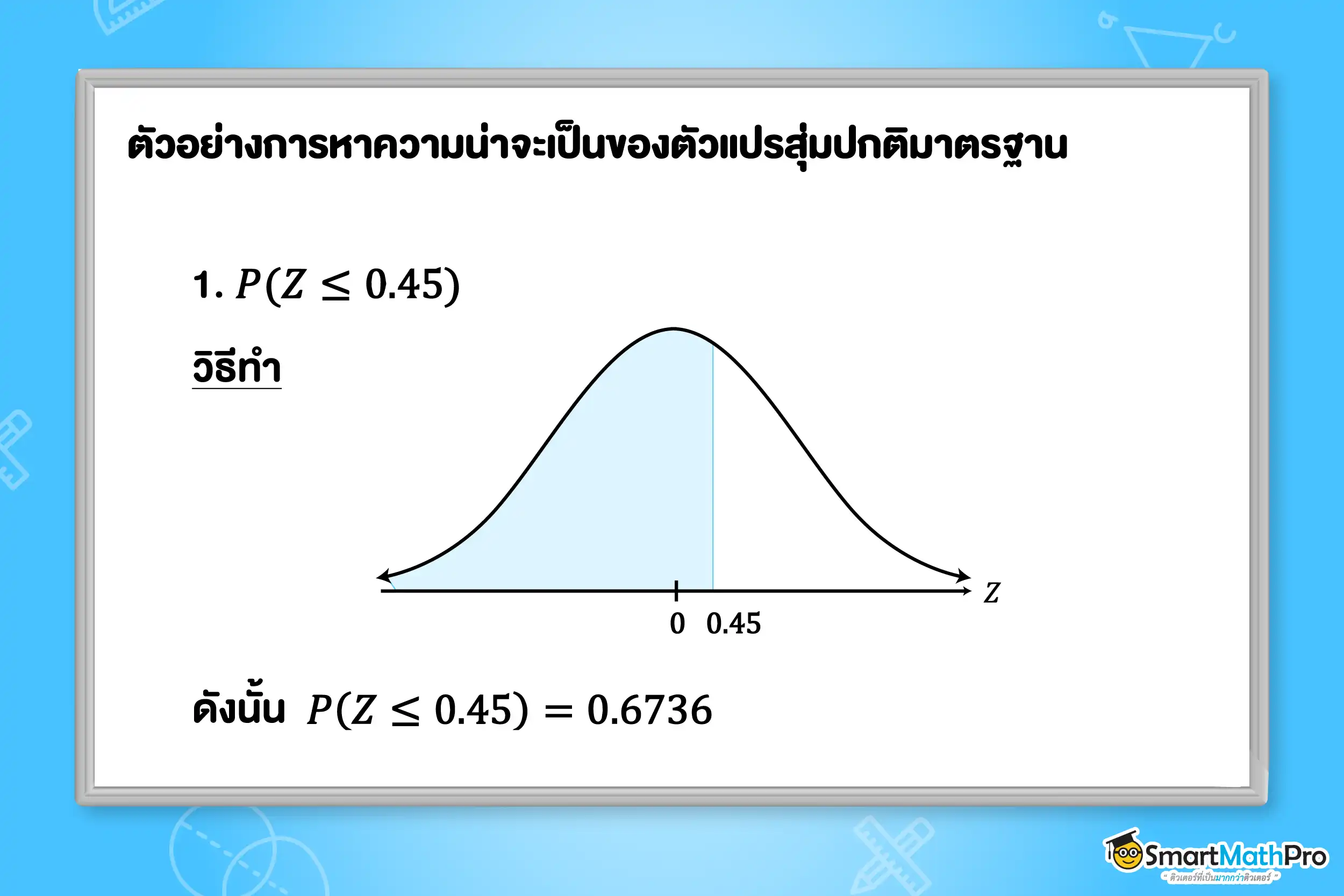
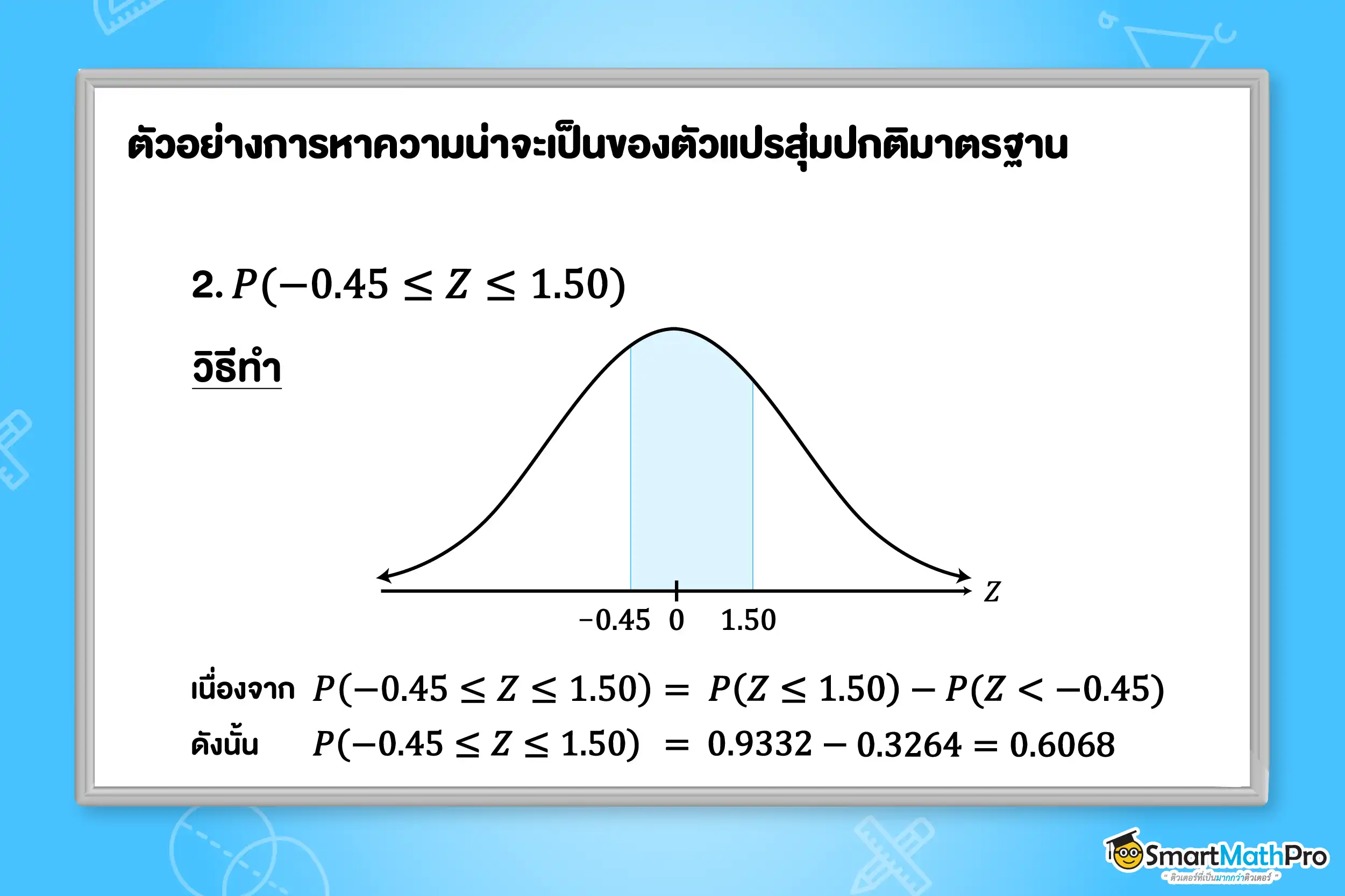
ค่าของตัวแปรสุ่มปกติมาตรฐาน
ค่าของตัวแปรสุ่มปกติมาตรฐาน สามารถหาได้จากสูตรต่อไปนี้
ตัวอย่างที่ 8 คะแนนสอบวิชาภาษาอังกฤษของนักเรียน ม.6/4 มีการแจกแจงปกติ โดยมีค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเท่ากับ 17 และ 3 คะแนนตามลำดับ จงหาค่าของตัวแปรสุ่มปกติมาตรฐานของคะแนนสอบภาษาอังกฤษของนักเรียนที่ได้ 26 คะแนน
วิธีทำ ให้ตัวแปรสุ่ม X คือคะแนนสอบวิชาภาษาอังกฤษของนักเรียน ม.6/4 จะได้ว่า ตัวแปรสุ่ม X มีการแจกแจงปกติ โดยที่ \mu=17 และ \sigma=3 และ พิจารณาผลสอบของนักเรียนที่ได้ 26 คะแนน
แทนค่าลงในสูตรจะได้ว่า Z=\frac{26-17}{3}=\frac{9}{3}=3
ดังนั้น ค่าของตัวแปรสุ่มปกติมาตรฐาน เท่ากับ 3
โดยค่าของตัวแปรสุ่มปกติมาตรฐานมีอีกสูตรหนึ่ง คือ
เราจะไปดูการใช้สูตรผ่านตัวอย่างต่อไปนี้กัน
ตัวอย่างที่ 9 สำนักวิจัยแห่งหนึ่งค่าใช้จ่ายในการใช้โทรศัพท์มือถือรายเดือนของคนในจังหวัดระยองมีการแจกแจงปกติ โดยค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเท่ากับ 450 และ 90 บาท ตามลำดับ ถ้าสุ่มคนจากจังหวัดนี้มาคนหนึ่ง จงหาความน่าจะเป็นที่สุ่มได้ผู้ค่าใช้จ่ายในการใช้โทรศัพท์มือถือระหว่าง 270 บาท และ 540 บาท ต่อเดือน
เมื่อกำหนดตารางแสดงพื้นที่ใต้เส้นโค้งปกติมาตรฐานดังนี้
วิธีทำ จากโจทย์จะได้ค่าเฉลี่ย \mu เท่ากับ 450 และ ส่วนเบี่ยงเบนมาตรฐาน \sigma เท่ากับ 90
พิจารณาที่ a=270 และ b=540 นั่นคือ P(270<X<540)
P(270<X<540)
= P\left ( \frac{270-450 }{90 }\leq Z\leq \frac{540-450 }{90 } \right )
= P\left ( -2\leq Z\leq 1 \right )
= P\left ( Z\leq 1 \right )-P\left ( Z\leq -2 \right )
= 0.8413 – 0.0228
= 0.8185
เปอร์เซ็นไทล์ของตัวแปรสุ่มต่อเนื่อง
โดยปกติเปอร์เซ็นไทล์ของข้อมูลเชิงปริมาณ จะวัดตำแหน่งที่ของข้อมูล โดยนำข้อมูลเรียงจากน้อยไปมากและแบ่งเป็น 100 ส่วนเท่ากัน เปอร์เซ็นไทล์ของตัวแปรสุ่มต่อเนื่อง จะวัดตำแหน่งที่ของค่าที่เป็นไปได้ของตัวแปรสุ่ม โดยนำข้อมูลเรียงจากน้อยไปมากและแบ่งเป็น 100 ส่วนเท่ากันนั่นเอง
ตัวอย่างที่ 10 ร้านข้าวแกงกะหรี่จัดการแข่งขันกินข้าวแกงกะหรี่จานยักษ์ ไตเติ้ลใช้เวลา 12.5 นาที ในการกินอาหารจนหมด โดยที่การแข่งขันครั้งนี้มีค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของเวลาเท่ากับ 8.1 และ 4 นาที ตามลำดับ ถ้าเวลาในการแข่งขันนี้มีการแจกแจงปกติ จงหาเปอร์เซ็นไทล์ของเวลาที่ไตเติ้ลใช้ในการแข่งขัน เมื่อกำหนดตารางแสดงพื้นที่ใต้เส้นโค้งปกติมาตรฐานดังนี้
แนวคิด เปอร์เซ็นไทล์ของเวลาที่ไตเติ้ลใช้ในการแข่งขัน หาได้จากพื้นที่ใต้เส้นโค้งปกติมาตรฐาน โดยหาค่าของตัวแปรสุ่มปกติมาตรฐานก่อน
วิธีทำ ให้ตัวแปรสุ่ม X คือเวลาที่ใช้ในการแข่งขันกินข้าวแกงกะหรี่จานยักษ์ จะได้ว่า ตัวแปรสุ่ม X มีการแจกแจงปกติ โดยที่ \mu=8.1 และ \sigma=4 และพิจารณาเวลาที่ไตเติ้ลใช้ในการแข่งขัน คือ 12.5 นาที
จาก Z=\frac{X-\mu }{\sigma }
Z=\frac{12.5-8.1 }{4 }=\frac{4.4 }{4 }=1.1
แสดงว่า P (Z<1.1) =0.86433
จะได้ว่า P (Z<1.1)\times100 =0.86433\times100=86.433
ดังนั้น เปอร์เซ็นไทล์ของเวลาที่ไตเติ้ลใช้ในการแข่งขัน ประมาณเปอร์เซ็นไทล์ที่ 86
การเปรียบเทียบตำแหน่งของข้อมูล
การแปลงตัวแปรสุ่มปกติให้เป็นตัวแปรสุ่มปกติมาตรฐาน นอกจากสามารถหาความน่าจะเป็นได้ (จากการเปิดตาราง)
ยังสามารถนำไปเปรียบเทียบข้อมูลสองชุดได้ด้วยน้า ลองดูผ่านตัวอย่างนี้กัน
ตัวอย่างที่ 11 ในการทำแบบทดสอบหลังเรียนวิชาภาษาไทยและวิชาสังคมของนักเรียนห้องหนึ่ง พบว่าคะแนนสอบทั้งสองวิชามีค่าเฉลี่ยเลขคณิตเท่ากัน คือ 28 คะแนน ถ้าคะแนนในการทำแบบทดสอบของแต่ละวิชามีการแจกแจงปกติ จงหาว่าซันนี่ซึ่งเป็นนักเรียนห้องนี้ทำข้อสอบวิชาใดได้ดีกว่ากัน เมื่อคะแนนสอบและส่วนเบี่ยงเบนมาตรฐานมีค่าดังตาราง
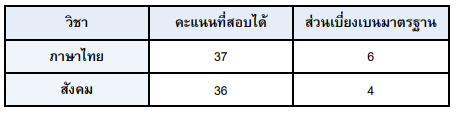
แนวคิด เปรียบเทียบค่าของตัวแปรสุ่มปกติมาตรฐานของทั้งสองคน แล้วพิจารณาว่าใครที่มีค่าตัวแปรสุ่มปกติมาตรฐานมากกว่า จะถือว่าทำข้อสอบได้ดีกว่า
วิธีทำ จาก Z=\frac{X-\mu }{\sigma }
ค่าตัวแปรสุ่มปกติมาตรฐานของคะแนนวิชาภาษาไทย คือ
Z=\frac{37-28 }{6 }=\frac{9}{6}=1.5
ค่าตัวแปรสุ่มปกติมาตรฐานของคะแนนวิชาสังคม คือ
Z=\frac{36-28 }{4 }=\frac{8}{4}=2
จะได้ว่า ค่าตัวแปรสุ่มปกติมาตรฐานของวิชาภาษาไทยได้น้อยกว่าค่าตัวแปรสุ่มปกติมาตรฐานของคะแนนวิชาสังคม
ดังนั้น ซันนี่ทำข้อสอบวิชาสังคมได้ดีกว่าวิชาภาษาไทย
ดูคลิปติวฟรี ตัวแปรสุ่มและการแจกแจงความน่าจะเป็น ม.6
คลิปติว ตัวแปรสุ่มและการแจกแจงความน่าจะเป็น ม.6 จาก SmartMathPro
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
บทตัวแปรสุ่มและการแจกแจงความน่าจะเป็น เป็นบทเรียนในคณิต ม.6 ที่น้อง ๆ จะได้เจอในชีวิตประจำวัน เช่น
การแจกแจงปกติมาตรฐานที่ใช้กับการประกาศคะแนนสอบ TCAS เพื่อให้คะแนนสอบของทุกคนเป็นคะแนนกลางและสามารถนำมาเปรียบเทียบกันได้
แต่นอกจากจะเป็นบทเรียนในโรงเรียนแล้วก็ยังเป็นบทที่ออกสอบ A-Level คณิต 1 ประมาณปีละ 2 ข้ออีกด้วย ดังนั้นพี่แนะนำให้น้อง ๆ เก็บเนื้อหาบทนี้ด้วยน้า โดยอาจจะเริ่มจากทบทวนจากการทำโจทย์บ่อย ๆ ให้ได้คล่องมือ และถ้าใครไม่รู้จะไปหาโจทย์จากไหนมาฝึกก็สามารถเข้าไปดาวน์โหลดข้อสอบตัวแปรสุ่มและการแจกจงความน่าจะเป็น ม.6 กันได้เลยย
เนื้อหาคณิตศาสตร์ ม.ปลาย อาจดูเป็นเรื่องยากในความคิดของน้อง ๆ หลายคน แต่ที่จริงถ้าเรามีพื้นฐานที่ดี ทบทวนบทเรียนและฝึกทำโจทย์บ่อย ๆ ก็จะทำให้เข้าใจในเนื้อหามากขึ้น แต่ถ้าใครยังกังวล กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ
จนทำให้เรียนบทอื่นต่อไม่ได้ อยากได้คนช่วยไกด์
พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากก เพราะแพ็กม.5 – ม.6 เรียนได้ถึง 2 ปี และแพ็ก ม.4 – ม.6 เรียนได้ถึง 3 ปี พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมาก นอกจากนี้ยังพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ และถ้าแพ็กไม่ตรงกับบทที่โรงเรียนสอนก็สามารถเลือกเป็นคอร์สแยกบทได้เพราะมีคอร์สติวแยกบทของคณิต ม.ปลายทุกบทเลย แน่นอนว่ามีส่วนลดพิเศษเช่นกันน้า ใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
แคลคูลัส ม.6 สรุปเนื้อหา โจทย์แคลคูลัสพร้อมวิธีทำ และคลิปติวฟรี
ลำดับและอนุกรม ม.6 สรุปเนื้อหาพร้อมตัวอย่างโจทย์และวิธีทำ
สถิติ ม.6 สรุปเนื้อหาสถิติและข้อมูล พร้อมโจทย์แบบจัดเต็ม ! - SmartMathPro
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
A-Level คณิต 1, A-Level คณิต 2 TCAS67 สอบอะไรบ้าง? อัปเดตล่าสุด
ข้อสอบ A-Level คณิต 1 และคณิต 2 67 ออกอะไรบ้าง ? พร้อมแจกบทน่าเก็บ
A Level คณิตศาสตร์ 1 กับ 2 ต่างกันยังไง? ยื่นคณะไหนได้บ้าง?
บทความ แนะนำ
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
Twitter : @PanSmartMathPro
Tiktok : @pan_smartmathpro
