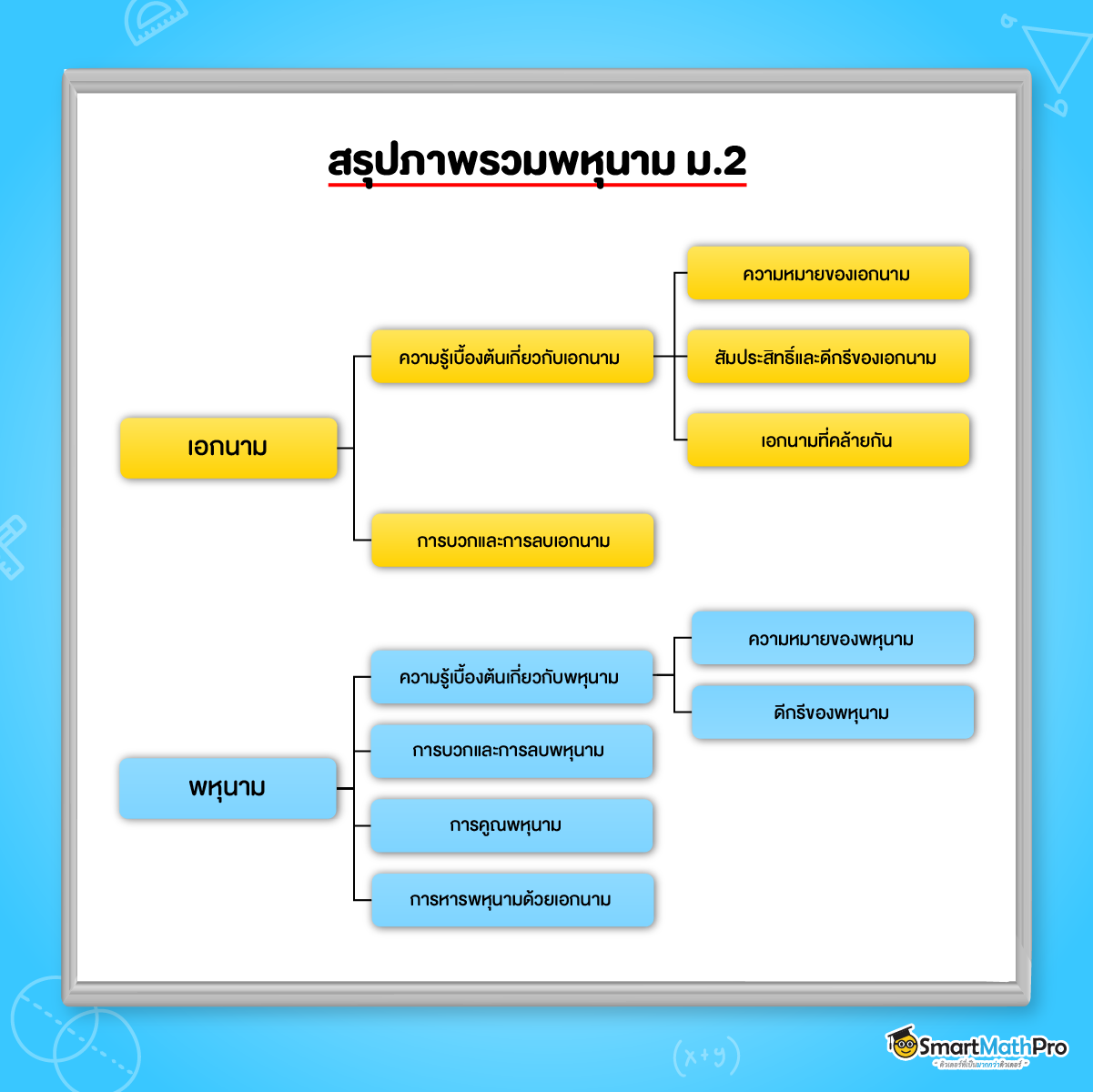
น้อง ๆ คนไหนกำลังหาสรุปเนื้อหาคณิตเรื่องพหุนาม ม.2 อยู่ บอกเลยว่าบทความนี้เหมาะมาก เพราะว่าพี่ได้ทำสรุปทั้งพหุนามและเอกนามซึ่งเป็นพื้นฐานของเอกนามกันด้วย โดยความรู้ที่ได้จากบทนี้จะถูกนำไปต่อยอดในบทอื่นอีกหลายบท และยิ่งไปกว่านั้น พี่ยังมีแจกแบบฝึกหัดและเฉลยเรื่องพหุนาม ม.2 ให้ฟรีอีก 10 ข้อที่ท้ายบทความด้วยน้าา
เอกนามคืออะไร ?
น้อง ๆ น่าจะเคยเรียนหรือเคยเห็นจำนวนที่เขียนอยู่ในรูปค่าคงตัวหรือตัวแปรที่อยู่ในรูปของการดำเนินการกัน (บวก ลบ คูณ หาร ยกกำลัง) มาแล้วใช่ไหมเช่น 5, 2x, x-y^2 โดยเราจะเรียกจำนวนเหล่านี้ว่า นิพจน์
ในหัวข้อนี้เราจะกล่าวถึง เอกนาม ซึ่งมีความหมายดังนี้
เอกนาม (monomial) คือ นิพจน์ที่สามารถเขียนให้อยู่ในรูปของการคูณกันของค่าคงตัวและตัวแปรตั้งแต่หนึ่งตัวขึ้นไป และเลขชี้กำลังของตัวแปรแต่ละตัวเป็นศูนย์หรือจำนวนเต็มบวก
จากความหมายของเอกนามในกรอบข้างต้น น้อง ๆ น่าจะพอสรุปกันได้แล้วใช่ไหมว่าจำนวนทุกจำนวนที่เราเรียกว่านิพจน์ อาจจะไม่ได้เป็นเอกนามเสมอไป เพราะนิพจน์ที่เป็นเอกนามได้นั้นจะต้องมีลักษณะตรงตามเงื่อนไข 2 ข้อ คือ
- สามารถเขียนให้อยู่ในรูปของการคูณกันของค่าคงตัวและตัวแปร
- เลขชี้กำลังของตัวแปรแต่ละตัวเป็นศูนย์หรือจำนวนเต็มบวก
พี่จะขอยกตัวอย่างนิพจน์ที่เป็นและไม่เป็นเอกนามผ่านตัวอย่างต่อไปนี้น้า
ตัวอย่างที่ 1 จงพิจารณาว่านิพจน์ต่อไปนี้เป็นเอกนามหรือไม่
จากตัวอย่างข้างต้น จะเห็นว่านิพจน์ในข้อ 1) และ 2) เป็นนิพจน์ที่มีตัวแปร x เพียงตัวเดียว และทั้งสองนิพจน์มีเลขชี้กำลังของตัวแปรเป็นบวก ส่วนนิพจน์ในข้อ 5) ถึงจะมีทั้งตัวแปร x และ y แต่ตัวแปรทั้งสองคูณกันและมีเลขชี้กำลังเป็นบวก ดังนั้น นิพจน์ในข้อที่ 1), 2) และ 5) จึงเป็นเอกนาม
ส่วนนิพจน์ในข้อ 3) เขียนในรูปของการบวกกันของตัวแปร x และ y ไม่ใช่การคูณกัน ขณะที่ข้อ 4) เลขชี้กำลังของ x เป็นจำนวนเต็มลบ ไม่ใช่จำนวนเต็มบวก ดังนั้นนิพจน์ในข้อ 3) และ 4) จึงไม่เป็นเอกนาม
สัมประสิทธิ์และดีกรีของเอกนาม
น้อง ๆ ที่อ่านจนถึงตรงนี้ น่าจะเห็นแล้วว่าในการพิจารณาว่านิพจน์ต่าง ๆ เป็นเอกนามหรือไม่ เราจะไม่ได้พิจารณาค่าคงตัวที่อยู่ด้านหน้าตัวแปรเลย
อย่างไรก็ตาม แม้ว่าเราจะไม่ได้พิจารณาความเป็นเอกนามจากค่าคงตัวนั้น แต่ค่าคงตัวก็เป็นองค์ประกอบหนึ่งที่สำคัญของเอกนาม โดยเอกนามจะมีคำศัพท์ที่ควรรู้ทั้งสิ้น 2 คำ ซึ่งมาจากการที่เอกนามประกอบด้วยสองส่วน คือ ตัวแปรหรือตัวแปรที่เขียนในรูปของการคูณ และค่าคงตัว คำศัพท์คำแรก เราจะเรียกส่วนที่เป็นค่าคงตัวนี้เราจะเรียกว่า สัมประสิทธิ์ (coefficient) ของเอกนาม
อีกคำศัพท์หนึ่งที่เกี่ยวข้องกับเอกนามที่น้อง ๆ ควรรู้จักก็คือ ดีกรี (degree) ของเอกนาม หมายถึง ผลบวกของเลขชี้กำลังของตัวแปรแต่ละตัวในเอกนาม ลองมาพิจารณาตัวอย่างต่อไปนี้กัน
เอกนามที่คล้ายกัน
เอกนามทั้งสองจะคล้ายกัน ก็ต่อเมื่อ
1. เอกนามทั้งสองมีตัวแปรชุดเดียวกัน และ
2. เลขชี้กำลังของตัวแปรเดียวกันในแต่ละเอกนามเท่ากัน
ตัวอย่างของเอกนามที่คล้ายกัน
- x คล้ายกันกับ 2x
- -2x^2yz^3 คล้ายกันกับ \frac{1}{2}x^2yz^3
ตัวอย่างของเอกนามที่ไม่คล้ายกัน
- x ไม่คล้ายกันกับ 2y
- a^2b^3 ไม่คล้ายกันกับ a^3b^2
การบวกและการลบเอกนาม
การหาผลบวกและผลลบของเอกนามที่คล้ายกันทำได้ดังนี้
- ผลบวกของเอกนามที่คล้ายกัน
= (ผลบวกของสัมประสิทธิ์) x (ส่วนที่อยู่ในรูปของตัวแปรหรือการคูณกันของตัวแปร) - ผลลบของเอกนามที่คล้ายกัน
= (ผลลบของสัมประสิทธิ์) x (ส่วนที่อยู่ในรูปของตัวแปรหรือการคูณกันของตัวแปร)
ตัวอย่างที่ 2 จงหาผลลัพธ์ของ 3xy^2+5xy^2
วิธีทำ 3xy^2+5xy^2=(3+5)xy^2=8xy^2
ตัวอย่างที่ 3 จงหาผลลัพธ์ของ 5mn-7mn-(-8mn)
วิธีทำ 5mn-7mn-(-8mn)=(5-7-(-8))mn=6mn
พหุนาม
พหุนามคืออะไร ?
จากหัวข้อก่อนหน้า ทุกคนได้รู้จักกับเอกนามกันไปแล้ว ในหัวข้อนี้พี่จะกล่าวถึงพหุนามและการดำเนินการของพหุนามกัน
พหุนาม (polynomial) คือ นิพจน์ที่อยู่ในรูปเอกนาม หรือเขียนอยู่ในรูปการบวกกันของเอกนามตั้งแต่สองเอกนามขึ้นไปได้
ตัวอย่างของพหุนาม เช่น 8.5, 3z, 4y-1, x^{2}+3, 5x^{2}+4x-7 เป็นต้น
เราสามารถบอกได้ว่า ถ้าพจน์ใดเป็นเอกนาม พจน์นั้นก็จะเป็นพหุนามด้วยนั่นเองงเพื่อความสะดวกในการอ้างอิง เราจะเรียกแต่ละเอกนามที่ปรากฏในพหุนามว่า พจน์ (term)
ในกรณีที่พหุนามนั้นมีเอกนามที่คล้ายกัน เราจะเรียกเอกนามที่คล้ายกันว่า พจน์ที่คล้ายกัน (like terms) เช่น
3x^{2}+5x-7+2x เป็นพหุนามที่มีพจน์ คือ 3x^{2}, 5x, 7, 2x และมี 5x และ 2x เป็นพจน์ที่คล้ายกัน
ในกรณีที่พหุนามมีบางพจน์เป็นพจน์ที่คล้ายกัน เราสามารถรวมพจน์ที่คล้ายกันเข้าด้วยกัน และเรียกพหุนามที่ไม่มีพจน์คล้ายกันเลยว่า พหุนามในรูปผลสำเร็จ (polynomial in the simplest form) โดยดีกรีของพหุนาม คือ ดีกรีสูงสุดของพจน์ของพหุนามในรูปผลสำเร็จ
การบวกและการลบพหุนาม
การบวกพหุนาม
การบวกพหุนามสามารถทำได้โดยนำพหุนามมาเขียนในรูปการบวก และถ้ามีพจน์ที่คล้ายกัน ให้บวกพจน์ที่คล้ายกันเข้าด้วยกัน ลองไปดูการบวกพหุนามผ่านตัวอย่างต่อไปนี้กัน
ตัวอย่างที่ 4 จงหาผลบวกของ 4x^{2}+x+6 และ 2x^{2}-3x-4
วิธีทำ \left ( 4x^{2}+x+6 \right ) +\left ( 2x^{2}-3x-4 \right ) \\ = 4x^{2}+x+6 +2x^{2}-3x-4 \\ = \left ( 4x^{2}+2x^{2} \right )+\left ( x-3x \right )+\left ( 6-4 \right ) \\ = 6x^{2}+\left ( -2x \right )+2 \\ = 6x^{2}-2x+2
การลบพหุนาม
ก่อนที่เราจะไปรู้จักการลบของพหุนาม พี่จะพาไปรู้จักกับ “พหุนามตรงข้าม” กันก่อน
พหุนามตรงข้าม คือ พหุนามที่นำไปบวกกับพหุนามที่กำหนด แล้วได้ผลลัพธ์เป็น 0
พิจารณาพหุนาม 2x ถ้านำ 2x+(-2x)=0 แล้วจะได้ว่า -2x เป็นพหุนามตรงข้ามของ 2x หรือตัวอย่างอื่น ๆ อีก เช่น
- x-1 มีพหุนามตรงข้ามคือ –(x-1)=-x+1
- x^{2}-x+2 มีพหุนามตรงข้ามคือ -(x^{2}-x+2)=-x^{2}+x-2
หรือเราสามารถมองง่าย ๆ ว่าพหุนามตรงข้ามคือพหุนามที่สลับเครื่องหมาย จากบวกเป็นลบ หรือจากลบเป็นบวก
การลบพหุนามด้วยพหุนาม ทำได้โดยบวกพหุนามตัวตั้งด้วยพหุนามตรงข้ามของพหุนามตัวลบ
พหุนามตัวตั้ง – พหุนามตัวลบ = พหุนามตัวตั้ง + พหุนามตรงข้ามของพหุนามตัวลบ
เพื่อให้น้อง ๆ เข้าใจมากขึ้นเราลองไปดูผ่านตัวอย่างนี้กัน
ตัวอย่างที่ 5 จงหาผลลบ \left ( 6x^{2}-2x+2 \right )-\left ( x^{2}-7x-5 \right )
วิธีทำ จากโจทย์ พหุนามตรงข้ามของ x^{2}-7x-5 คือ -x^{2}+7x+5
จะได้ว่า \left ( 6x^{2}-2x+2 \right )-\left ( x^{2}-7x-5 \right ) \\
= \left ( 6x^{2}-2x+2 \right )+\left ( -x^{2}+7x+5 \right ) \\
= \left ( 6x^{2}-x^{2}\right )+\left ( -2x+ 7x\right )+\left ( 2+5 \right ) \\
= 5x^{2}+5x+ 7
การคูณพหุนาม
ในหัวข้อนี้เราจะกล่าวถึงการคูณระหว่างเอกนามกับเอกนาม การคูณระหว่างเอกนามกับพหุนาม และการคูณระหว่าง
พหุนามกับพหุนาม โดยสามารถนำสมบัติต่าง ๆ ที่เคยเรียนมาแล้ว ได้แก่สมบัติเลขยกกำลัง สมบัติการบวกและการคูณของจำนวนจริง สมบัติการสลับที่ สมบัติการเปลี่ยนหมู่ สมบัติการแจกแจง รวมถึงสมบัติของหนึ่งและศูนย์ มาใช้ในการหาผลคูณได้ด้วย
การคูณระหว่างเอกนามกับเอกนาม เป็นหัวข้อที่ไม่ซับซ้อน สามารถหาผลคูณได้โดยการนำค่าคงตัวในแต่ละเอกนามมาคูณกัน และนำตัวแปรในแต่ละเอกนามมาคูณกัน โดยใช้สมบัติของเลขยกกำลัง เช่น
- (3)(6x)=(3\times 6)x=18x
- (xy^{2})(y^{3})=xy^{2+3}=xy^{5}
การคูณระหว่างเอกนามกับพหุนาม
การหาผลคูณระหว่างเอกนามกับพหุนาม สามารถทำได้โดยใช้สมบัติการแจกแจง โดยที่เอกนามคูณจะเข้าไปในแต่ละพจน์ของพหุนาม และใช้หลักการคูณเอกนามที่พี่บอกไว้ก่อนหน้านี้
ตัวอย่างที่ 6 จงหาผลคูณ (2x)(-3x+5)
วิธีทำ (2x)(-3x+5)=(2x)(-3x)+(2x)(5)\\
= -6x^{2}+10x
การคูณระหว่างพหุนามกับพหุนาม ทำได้โดยคูณแต่ละพจน์ของพหุนามหนึ่งกับทุก ๆ พจน์ของอีกพหุนามหนึ่ง แล้วนำผลคูณของแต่ละพจน์นั้นมาบวกกันให้เป็นพหุนามในรูปผลสำเร็จ
ตัวอย่างที่ 7 จงหาผลคูณ (x-2)(2x^{2}+3x)
วิธีทำ (x-2)(2x^{2}+3x) \\ =(x)(2x^{2})+(x)(3x)-(2)(2x^{2})-(2)(3x) \\ =2x^{3}+3x^{2}-4x^{2}-6x \\ =2x^{3}-x^{2}-6x
การหารพหุนามด้วยเอกนาม
สำหรับ ม.2 เราจะพูดถึงการหารพหุนามด้วยเอกนามเท่านั้น ส่วนการหารพหุนามด้วยพหุนามจะอยู่ในม.ปลายน้า
ในการหารพหุนามด้วยเอกนาม เรามีข้อตกลงว่าเอกนามที่เป็นตัวหารจะต้องไม่เป็นศูนย์เสมอ พื้นฐานในการหารพหุนามด้วยเอกนามนั้น คือ การหารเอกนามด้วยเอกนาม ซึ่งน้อง ๆ สามารถทำได้โดยใช้สมบัติเลขยกกำลัง เช่น
- 6x^{3}\div 3x^{2}=\frac{6x^{3}}{3x^{2}}=2x^{3-2}=2x
- x^{3}y^{4}\div xy^{3}=\frac{x^{3}y^{4}}{ xy^{3}}=x^{2}y
หลังจากที่น้อง ๆ รู้พื้นฐานแล้ว เราจะนำมาใช้ในการหารพหุนามด้วยเอกนาม ทำได้โดยการหารแต่ละพจน์ของพหุนามด้วยเอกนาม แล้วนำผลหารนั้นมาบวกกัน (เมื่อได้ผลหารเป็นพหุนาม) ซึ่งเป็นไปตามความสัมพันธ์
ตัวหาร x ผลหาร = ตัวตั้ง
ถ้าเราตรวจสอบผลหารแล้วเป็นไปตามความสัมพันธ์นี้ แสดงว่าผลหารถูกต้อง
ตัวอย่างที่ 8 จงหาร 6x^{3}-15x^{2} ด้วย -3x
วิธีทำ \frac{6x^{3}-15x^{2}}{-3x} \\ = \frac{6x^{3}}{-3x}-\frac{15x^{2}}{-3x} \\ = -2x^{2}+5x
เป็นอย่างไรกันบ้างสำหรับเนื้อหาของพหุนาม ม.2 และอย่างที่พี่กล่าวไปข้างต้นว่าเนื้อหานี้จะถูกนำไปต่อยอดในบทอื่น ๆ เช่น การแยกตัวประกอบของพหุนามดีกรีสอง การแยกตัวประกอบของพหุนามดีกรีสูงกว่าสอง สมการกำลังสองตัวแปรเดียว และกราฟของฟังก์ชันกำลังสอง
นอกจากยังเป็นพื้นฐานสำคัญในการเรียนคณิตศาสตร์ระดับชั้น ม.ปลาย อีกด้วย ดังนั้นการทบทวนเนื้อหาให้แม่นและฝึกทำโจทย์ / แบบฝึกหัดเรื่องพหุนาม ม.2 ให้แม่น เป็นเรื่องที่สำคัญมากน้าา
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
สรุปเนื้อหา เส้นขนาน ม.2 พร้อมแจกโจทย์ให้ฝึกทำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
คณิตศาสตร์ ม.3 เทอม 1, เทอม 2 เรียนอะไรบ้าง ? อัปเดตตาม สสวท.
สรุปพื้นฐาน การแยกตัวประกอบของพหุนาม พร้อมตัวอย่างโจทย์และเฉลย
สรุปพื้นฐาน ทฤษฎีบทพีทาโกรัส แบบเข้าใจง่ายพร้อมตัวอย่างโจทย์
เลขยกกำลัง คืออะไร? สรุปเนื้อหาพร้อมแจกตารางเลขยกกำลังที่ควรรู้
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
