น้อง ๆ ม.2 อาจจะเคยได้ยินชื่อ การแยกตัวประกอบพหุนามดีกรีสอง กันมาบ้าง เพราะเป็นเนื้อหาคณิตศาสตร์ ม.2 ที่
ทุกคนต้องได้เรียน แต่บางคนก็อาจจะยังไม่เข้าใจเนื้อหาบทนี้ ยังจำสูตรไม่ได้ หรือแก้โจทย์ไม่เป็นอยู่
วันนี้พี่เลยขอมาสรุปเนื้อหาเรื่องนี้ให้น้อง ๆ อ่านกันแบบเข้าใจง่ายที่สุด พร้อมมีแบบฝึกหัดและเฉลยให้ไปฝึกทำเพิ่มเติมที่ท้ายบทความด้วย อย่ารอช้า ไปอ่านกันเลยดีกว่าาา
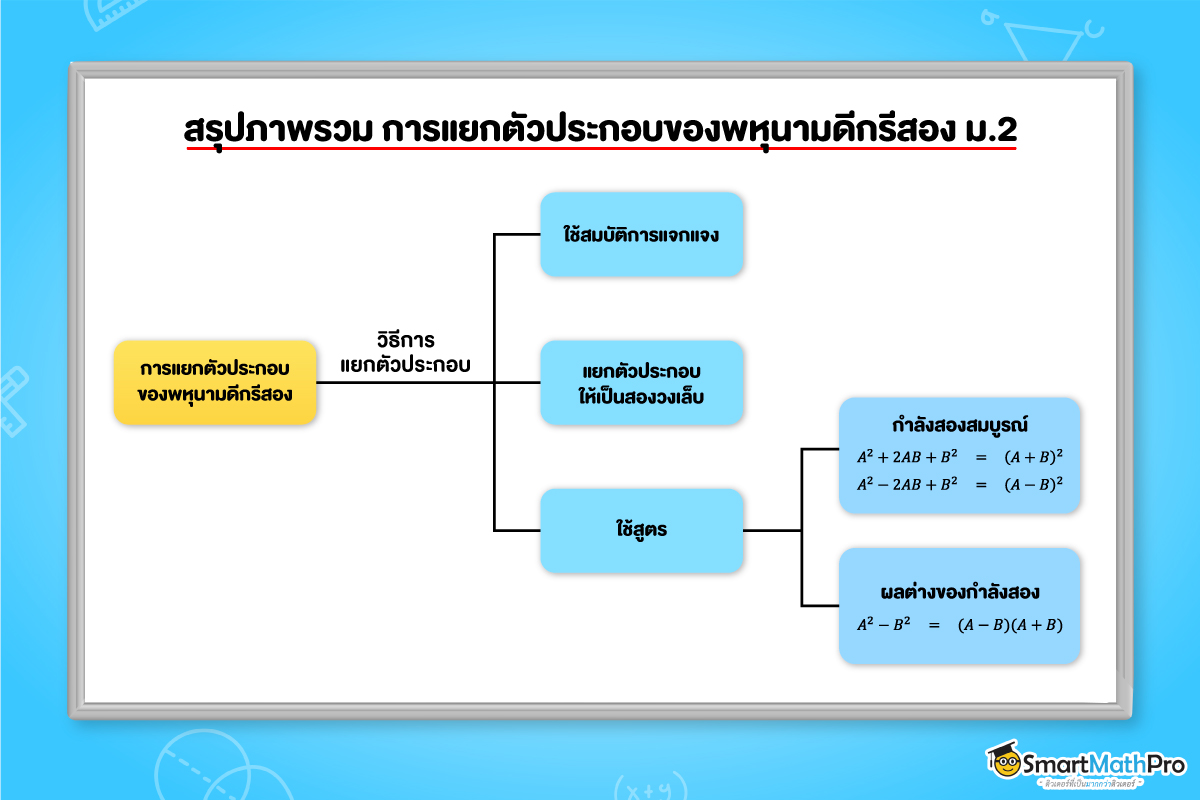
การแยกตัวประกอบของพหุนามดีกรีสอง คืออะไร ?
น้อง ๆ หลายคนน่าจะเคยได้เรียนเรื่องการคูณพหุนามกันมาแล้ว ยังจำกันได้อยู่ไหมว่าถ้าเรานำพหุนามดีกรีหนึ่ง 2 ตัว มาจับคูณกัน จะได้ผลคูณที่เป็นพหุนามดีกรีสอง แต่บทความนี้เราจะทำกระบวนการย้อนกลับ นั่นคือเราจะแยกพหุนามดีกรีสอง ให้กลับไปเป็นผลคูณของพหุนามดีกรีหนึ่ง 2 ตัว ซึ่งกระบวนการนี้เรียกว่า “การแยกตัวประกอบของพหุนามดีกรีสอง”
บทนี้ถือเป็นบทสำคัญมากเลย เพราะจะช่วยให้เราจัดรูปพหุนามได้ง่ายขึ้น ทำให้เราสามารถแก้สมการหรือวิเคราะห์คุณสมบัติต่าง ๆ สะดวกยิ่งขึ้น อีกทั้งยังเป็นพื้นฐานของบทอื่น ๆ ในระดับชั้นมัธยมศึกษาตอนต้น เช่น การแยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง, สมการกำลังสองตัวแปรเดียว และกราฟของฟังก์ชันกำลังสอง นอกจากนี้ยังเป็นพื้นฐานของความรู้ที่จะใช้ในระดับชั้นมัธยมศึกษาตอนปลายด้วย
น้อง ๆ ลองพิจารณาผลคูณของพหุนาม 3x กับ x+2 จะได้ว่า 3x(x+2)=(3x)(x)+(3x)(2)=3x^{2}+6x ในทางกลับกัน แสดงว่า 3x^{2}+6x=3x(x+2) ดังนั้น พหุนาม 3x^{2}+6x จะแยกตัวประกอบได้เป็น 3x(x+2) จากการกระจายพหุนามของตัวอย่างข้างต้น จะพบว่า การแยกตัวประกอบของพหุนามคือการทำขั้นตอนย้อนกลับของการคูณพหุนามนั่นเอง
โดยการแยกตัวประกอบของหัวข้อนี้ เราจะสนใจพหุนามดีกรีสองที่อยู่ในรูป ax^2+bx+c เมื่อ a, b, c เป็นจำนวนเต็ม และ a\neq 0 เพื่อความสะดวกเราจะเรียก ax^2 ว่าพจน์หน้า เรียก bx ว่าพจน์กลาง และ เรียก c ว่าพจน์หลัง
วิธีการแยกตัวประกอบของพหุนามดีกรีสองตัวแปรเดียว
ในหัวข้อนี้ พี่จะขอนำเสนอวิธีแยกตัวประกอบของพหุนามดีกรีสองทั้งหมด 5 รูปแบบ
รูปแบบที่ใช้สมบัติการแจกแจง
สมบัติการแจกแจง (การดึงตัวร่วม)
ให้ a, b และ c เป็นจำนวนใด ๆ
จะได้ว่า ab+ac=a(b+c) หรือ ba+ca=(b+c)a
จากสมบัติข้างต้นเราจะเรียก a ว่า ตัวประกอบร่วม หรือเรียกสั้น ๆ ว่า ตัวร่วม นั่นเอง เรามาพิจารณาวิธีการแยกตัวประกอบของ x^2+2x โดยใช้สมบัติการแจกแจงเพื่อทำความเข้าใจการใช้ สมบัตินี้กันดีกว่า
ตัวอย่างที่ 1 จงแยกตัวประกอบของ x^2+5x
วิธีทำ จะสังเกตว่า ทั้งสองพจน์ที่โจทย์กำหนดมี x เป็นตัวร่วม
ดังนั้น x^2+5x=x(x)+5(x)=x(x+5)
ตัวอย่างที่ 2 จงแยกตัวประกอบของ 6y^{2}-4y
วิธีทำ จะสังเกตว่า ทั้งสองพจน์ที่โจทย์กำหนดมี 2y เป็นตัวร่วม
ดังนั้น 6y^{2}-4y=3y(2y)-2(2y)=2y(3y-2)
รูปแบบ ax^2+bx+c เมื่อ a=1
ลองสังเกตผลคูณของพหุนาม x+3 กับ x+4
(x+3)(x+4)=(x)(x)+(4)(x)+(3)(x)+(3)(4)\\ \,=x^{2}+4x+3x+12\\ \,=x^{2}+7x+12
จะเห็นว่า
- พจน์หน้าของผลลัพธ์เกิดจากการคูณกันระหว่าง x กับ x
- พจน์กลางของผลลัพธ์เกิดจากการบวกกันระหว่าง 4 กับ 3 แล้วคูณด้วย x
- พจน์หลังของผลลัพธ์เกิดจากการคูณกันระหว่าง 4 กับ 3
แสดงว่า
ถ้าจะแยกตัวประกอบของ x^{2}+7x+12 เราจะต้องหาจำนวนใด ๆ สองจำนวนที่
- บวกกันได้ 7 และ
- คูณกันได้ 12
สรุปได้ว่า
เทคนิคการแยกตัวประกอบของพหุนาม x^2+bx+c ให้เป็นสองวงเล็บ
สำหรับพหุนามดีกรีสองในรูป x^2+bx+c เมื่อ b, c เป็นจำนวนเต็ม และ c\neq0
ถ้า m และ n เป็นจำนวนเต็มสองจำนวน ซึ่ง mn=c และ m+n=b
จะได้ว่า x^2+bx+c=(x+m)(x+n)
ตัวอย่างที่ 3 จงแยกตัวประกอบของ x^2+x-20
วิธีทำ จากหลักการข้างต้น จะต้องหาจำนวน 2 จำนวนที่
- บวกกันได้ 1
- คูณกันได้ -20
เนื่องจาก 5+(-4)=1 และ 5\times(-4)=-20
แสดงว่า x^2+x-20=x^2+[(5)+(-4)]x+(5)(-4)
ดังนั้น x^2+x-20=(x+5)(x-4)
รูปแบบ ax^2+bx+c เมื่อ a\neq 1
ลองสังเกตผลคูณของพหุนาม 2x+3 กับ x+5
(2x+3)(x+5)=(2x+3)(x)+(2x+3)(5)\\=(2x^{2}+3x)+(10x+15)\\=2x^{2}+3x+10x+15\\=2x^{2}+13x+15
ดังนั้น แยกตัวประกอบของ 2x^{2}+13x+15 ได้ดังนี้ 2x^{2}+13x+15=(2x+3)(x+5)
จากผลคูณข้างต้น สามารถเขียนแผนภาพแสดงวิธีหาพจน์แต่ละพจน์ได้ดังนี้
ถ้าหาจำนวนตามเงื่อนไขทั้ง 3 ได้ ก็จะสามารถแยกตัวประกอบพหุนามที่อยู่ในรูป ax^2+bx+c ได้
เราลองมาดูตัวอย่างเพิ่มเติมกันเลย
ตัวอย่างที่ 4 จงแยกตัวประกอบของ 3x^2-7x+2
วิธีทำ จากหลักการข้างต้น จะต้องหาจำนวน 4 จำนวนที่
- หน้าคูณหน้า เท่ากับ 3
- หลังคูณหลัง เท่ากับ 2
- ใกล้คูณใกล้บวกไกลคูณไกล เท่ากับ -7
เนื่องจาก 3\times1=3, (-1)\times(-2)=2 และ (-1)(1)+(3)(-2)=(-1)+(-6)=-7
แสดงว่า 3x^2-7x+2=(3)(1)x^2+[(-1)(1)+(3)(-2)]x+(-1)(-2)
ดังนั้น 3x^2-7x+2=(3x-1)(x-2)
ตัวอย่างที่ 5 จงแยกตัวประกอบของ -2x^2-x+3
วิธีทำ สังเกตได้ว่าพหุนามตัวหน้ามีสัมประสิทธิ์ที่ติดลบ ดังนั้นเราจะทำการดึงตัวร่วมนั่นก็คือ -1 ออกมาก่อน
จะได้ว่า -2x^2-x+3=(-1)(2x^2)+(-1)(x)+(-1)(-3)\\ =(-1)(2x^{2}+x-3) แล้วนำ 2x^2+x-3 มาแยกตัวประกอบด้วยวิธีข้างต้น
จากหลักการข้างต้น จะต้องหาจำนวน 4 จำนวนที่
- หน้าคูณหน้า เท่ากับ 2
- หลังคูณหลัง เท่ากับ -3
- ใกล้คูณใกล้บวกไกลคูณไกล เท่ากับ 1
เนื่องจาก 2\times1=2, 3\times(-1)=-3 และ (3)(1)+(2)(-1)=(3)+(-2)=1
แสดงว่า 2x^2+x-3=(2)(1)x^2+[(3)(1)+(2)(-1)]x+(3)(-1)
ดังนั้น -2x^2-x+3=-(2x+3)(x-1)
รูปแบบการแยกด้วยกำลังสองสมบูรณ์
ลองสังเกตผลคูณของพหุนาม (x+3)^{2}
(x+3)^{2}=(x+3)(x+3)\\=(x+3)(x)+(x+3)(3)\\=x^{2}+(x)(3)+(x)(3)+3^{2}\\=x^{2}+(2)(x)(3)+3^{2}
จาก (x+3)^{2}=x^{2}+(2)(x)(3)+3^{2}
ถ้า x เป็นพจน์หน้า และ 3 เป็นพจน์หลัง
จะเขียนความสัมพันธ์นี้ได้ว่า (พจน์หน้า+พจน์หลัง)^{2}=(พจน์หน้า )^{2}+2(พจน์หน้า)(พจน์หลัง)+(พจน์หลัง)^{2}
และเป็นแบบนี้กับเครื่องหมายลบด้วยเช่นกัน
จึงสรุปเป็นสูตรได้ดังนี้
สูตร กำลังสองสมบูรณ์
กำหนดให้ A แทนพจน์หน้า และ B แทนพจน์หลัง จะได้ว่า
A^2+2AB+B^2=(A+B)^2
A^2-2AB+B^2=(A-B)^2
ตัวอย่างที่ 6 จงแยกตัวประกอบของ x^2-8x+16
วิธีทำ พิจารณา x^2-8x+16=(x)^2-2(x)(4)+(4)^2
แสดงว่า x เป็นพจน์หน้า และ 4 เป็นพจน์หลัง
จะได้ว่า x^2-8x+16=(x-4)^2
ตัวอย่างที่ 7 จงแยกตัวประกอบของ 4x^2+4x+1
วิธีทำ พิจารณา 4x^2+4x+1=(2x)^2+2(2x)(1)+(1)^2
แสดงว่า 2x เป็นพจน์หน้า และ 1 เป็นพจน์หลัง
จะได้ว่า 4x^2+4x+1=(2x+1)^2
รูปแบบการแยกด้วยผลต่างของกำลังสอง
ลองสังเกตผลคูณของพหุนาม (x-3) กับ (x+3)
(x-3)(x+3)=(x-3)(x)+(x-3)(3)\\=x^{2}-(3)(x)+(3)(x)-(3)^{2}\\=x^{2}-3^{2}
จาก (x-3)(x+3)=x^{2}-3^{2} หรือ x^{2}-3^{2}=(x-3)(x+3)
ถ้า x เป็นพจน์หน้า และ 3 เป็นพจน์หลัง
จะเขียนความสัมพันธ์นี้ได้ว่า (พจน์หน้า)^{2}-(พจน์หลัง)^{2}=(พจน์หน้า–พจน์หลัง)(พจน์หน้า+พจน์หลัง)
จึงสรุปเป็นสูตรได้ดังนี้
สูตร ผลต่างของกำลังสอง
กำหนดให้ A แทนพจน์หน้า และ B แทนพจน์หลัง จะได้ว่า
A^2-B^2=(A-B)(A+B)
ตัวอย่างที่ 8 จงแยกตัวประกอบของ x^2-25
วิธีทำ พิจารณา x^2-25=(x)^2-(5)^2
แสดงว่า x เป็นพจน์หน้า และ 5 เป็นพจน์หลัง
จะได้ว่า x^2-25=(x-5)(x+5)
ตัวอย่างที่ 9 จงแยกตัวประกอบของ 16x^2-9
วิธีทำ พิจารณา 16x^2-9=(4x)^2-(3)^2
แสดงว่า 4x เป็นพจน์หน้า และ 3 เป็นพจน์หลัง
จะได้ว่า 16x^2-9=(4x-3)(4x+3)
รวมสูตรในการแยกตัวประกอบของพหุนามดีกรีสอง
อ่านมาจนถึงตรงนี้ พี่เชื่อว่าน้อง ๆ หลายคนคงจะเข้าใจเรื่อง การแยกตัวประกอบของพหุนามดีกรีสอง ม.2 มากขึ้นแล้ว
ใช่ไหม แต่ถ้าใครอยากเก่งเรื่องนี้ขึ้นไปอีก พี่แนะนำให้ฝึกทำโจทย์ / แบบฝึกหัดการแยกตัวประกอบของพหุนามดีกรีสองเพิ่มเติมด้วยน้า รับรองว่าน้อง ๆ จะเข้าใจเนื้อหาบทนี้มากขึ้นแน่นอน และสำหรับบทความหน้าพี่จะมาสรุปเนื้อหาคณิต ม.2 เรื่องอะไรให้น้อง ๆ อ่านกันอีก รอติดตามกันน้าาา
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
สรุปเนื้อหา เส้นขนาน ม.2 พร้อมแจกโจทย์ให้ฝึกทำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
คณิตศาสตร์ ม.3 เทอม 1, เทอม 2 เรียนอะไรบ้าง ? อัปเดตตาม สสวท.
สรุปพื้นฐาน การแยกตัวประกอบของพหุนาม พร้อมตัวอย่างโจทย์และเฉลย
สรุปพื้นฐาน ทฤษฎีบทพีทาโกรัส แบบเข้าใจง่ายพร้อมตัวอย่างโจทย์
เลขยกกำลัง คืออะไร? สรุปเนื้อหาพร้อมแจกตารางเลขยกกำลังที่ควรรู้
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
