เส้นขนาน หมายถึง เส้นตรงสองเส้นที่อยู่บนระนาบเดียวกัน มีระยะห่างระหว่างสองเส้นเท่ากัน และไม่ตัดกัน ซึ่งน้อง ๆ สามารถเจอเส้นขนานในชีวิตจริงได้จากหลายอย่าง ไม่ว่าจะเป็น ถนน, รางรถไฟ, โต๊ะ, เก้าอี้, ประตู, หน้าต่าง และเรื่อง
เส้นขนานก็ยังเป็นเรื่องที่น้อง ๆ ต้องเรียนในคณิต ม.2 ด้วย
ซึ่งบทความนี้จะพาน้อง ๆ ไปเจาะลึกเนื้อหา เส้นขนาน ม.2 ทั้งเรื่องของความหมาย, สมบัติของเส้นขนาน, มุมต่าง ๆ พร้อมพาทำโจทย์ที่เกี่ยวกับเส้นขนาน และท้ายบทความยังมีแจกแบบฝึกหัดฟรีด้วย ถ้าพร้อมแล้วไปอ่านกันเลยยย
บทนิยาม
เส้นตรงสองเส้นที่อยู่บนระนาบเดียวกัน ขนานกัน ก็ต่อเมื่อ เส้นตรงทั้งสองเส้นนั้นไม่ตัดกัน
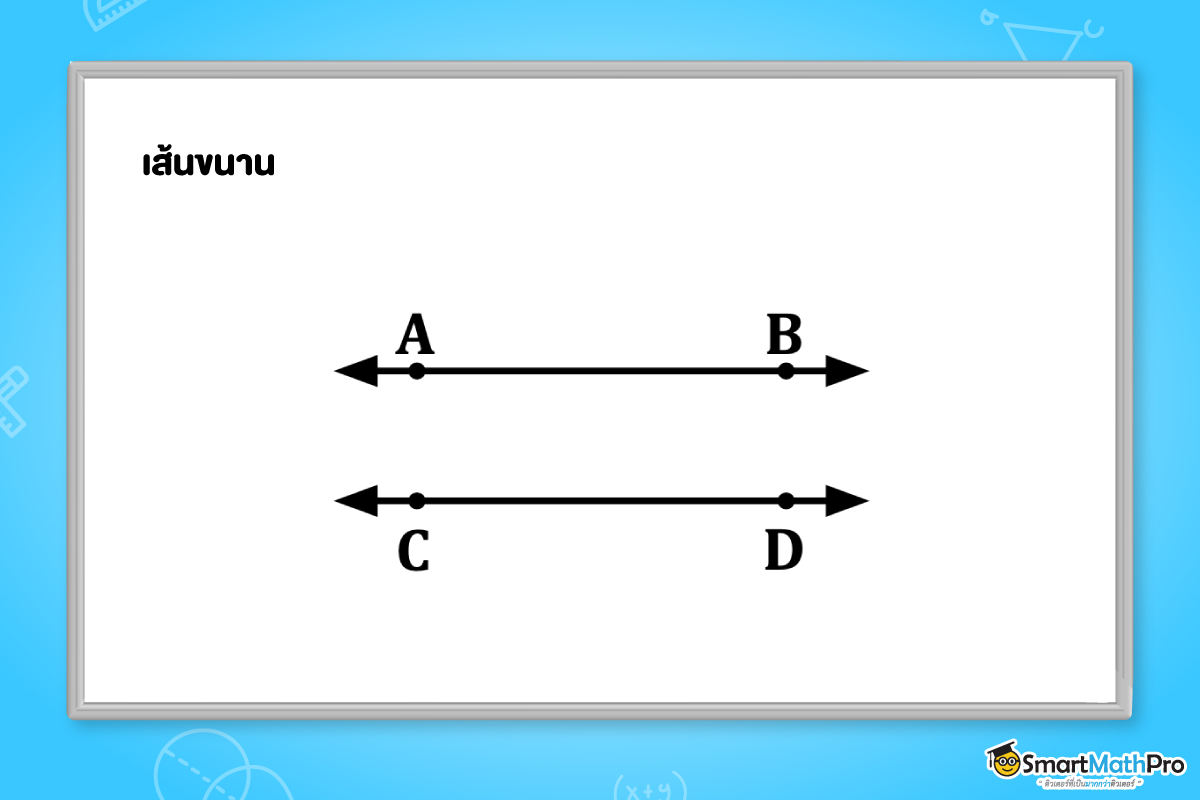
จากรูป เราจะเห็นว่า \overleftrightarrow{AB} และ \overleftrightarrow{CD} ขนานกัน ซึ่งเราสามารถบอกว่า \overleftrightarrow{AB} ขนานกับ \overleftrightarrow{CD} หรือ \overleftrightarrow{CD} ขนานกับ \overleftrightarrow{AB} ได้เช่นเดียวกัน และเขียนแทนได้ด้วยสัญลักษณ์ \overleftrightarrow{AB} // \overleftrightarrow{CD} หรือ \overleftrightarrow{CD} // \overleftrightarrow{AB}
ระยะห่างระหว่างเส้นขนาน
เราลองสังเกตเส้นตรง 2 เส้นที่ไม่ขนานกัน จะเห็นว่าระยะห่างระหว่างเส้นตรง 2 เส้นนั้นจะไม่เท่ากัน บางช่วงเส้นตรงเข้าใกล้กัน ระยะห่างดูน้อย บางช่วงเส้นตรงไกลกัน ระยะห่างดูมาก แต่ว่าถ้าเส้นตรงสองเส้นขนานกัน แล้วระยะห่างระหว่างเส้นตรงคู่นั้นจะเท่ากันเสมอ
ในทางกลับกัน ถ้าเส้นตรงสองเส้นมีระยะห่างระหว่างเส้นตรงเท่ากันเสมอ แล้วเส้นตรงคู่นั้นจะขนานกัน
มุมต่าง ๆ ที่เกี่ยวข้องกับเส้นขนาน
เราสามารถตรวจสอบได้ว่าเส้นตรงคู่ใดขนานกันบ้าง นอกจากการใช้บทนิยามของเส้นขนานและระยะห่างระหว่างเส้นตรงสองเส้นว่าคงที่หรือไม่ แล้วยังสามารถตรวจสอบโดยพิจารณาจากขนาดของมุมภายใน (interior angle), มุมแย้ง (alternate angle) หรือมุมภายนอก (exterior angle)
ซึ่งมุมเหล่านี้เกิดจากเส้นตรงเส้นหนึ่งมาตัดเส้นตรงคู่นั้น เรียกเส้นตรงนั้นว่า เส้นตัดขวาง (transversal) หรือเรียกสั้น ๆ ว่า เส้นตัด เพื่อให้น้อง ๆ เข้าใจมากขึ้น เราไปทำความรู้จักมุมต่าง ๆ จากรูปต่อไปกันเลยย
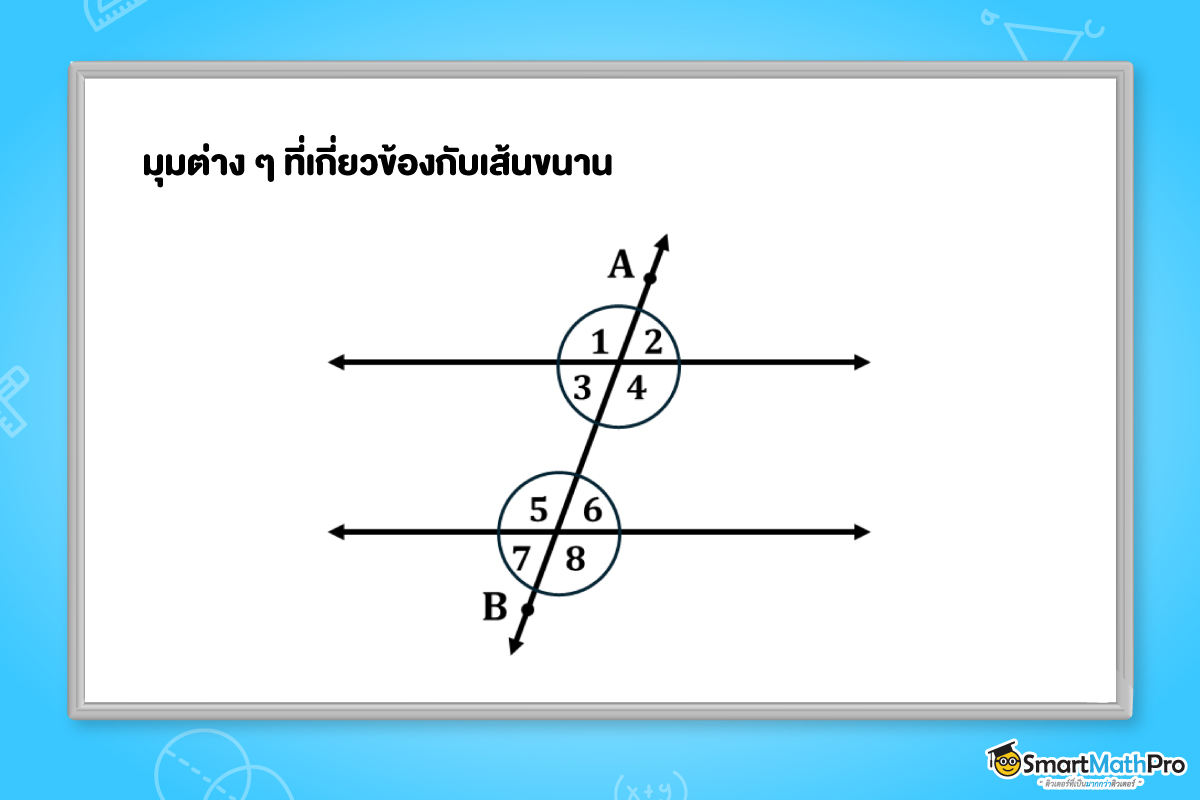
จากรูป เราเรียก \overleftrightarrow{AB} ว่า เส้นตัด AB
มุมภายใน ได้แก่ \widehat{3},\widehat{4},\widehat{5},\widehat{6}
มุมภายนอก ได้แก่ \widehat{1},\widehat{2},\widehat{7},\widehat{8}
เรียก \widehat{3} และ \widehat{6} ว่าเป็นมุมแย้งกัน และในทำนองเดียวกันกับคู่มุม \widehat{4} และ \widehat{5}
เรียก \widehat{3} และ \widehat{5} ว่า มุมภายในที่อยู่บนข้างเดียวกันของเส้นตัด และในทำนองเดียวกันกับคู่มุม \widehat{4} และ \widehat{6}
เรียก \widehat{1} และ \widehat{5} ว่า มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัด และในทำนองเดียวกันกับคู่มุม
ต่อไปนี้ \widehat{2} และ \widehat{6} , \widehat{7} และ \widehat{3} , \widehat{8} และ \widehat{4}
สมบัติของเส้นขนาน
เมื่อเส้นตรงเส้นหนึ่งตัดเส้นตรงคู่หนึ่ง เส้นตรงคู่นั้นขนานกัน ก็ต่อเมื่อ ขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้น ตัดรวมกันเท่ากับ 180 องศา
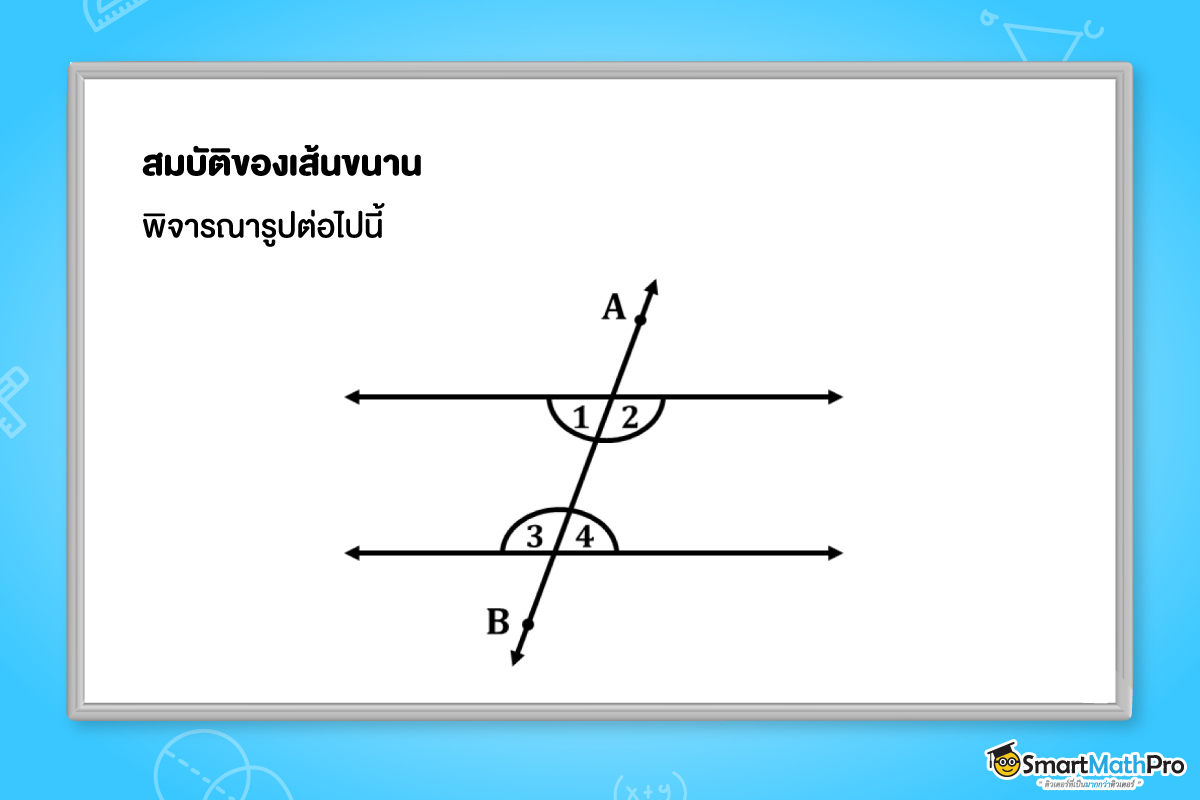
จากรูป ถ้าคู่ \widehat{1} และ \widehat{3} หรือคู่ \widehat{2} และ \widehat{4} รวมกันเท่ากับ 180 องศา แล้วเส้นตรงคู่นั้นจะขนานกัน
ในทางกลับกัน ถ้าเส้นตรงคู่นี้ขนานกัน แล้วคู่ \widehat{1} และ \widehat{3} หรือคู่ \widehat{2} และ \widehat{4} จะรวมกันเท่ากับ 180 องศาด้วย
เส้นขนานกับมุมแย้ง
ทฤษฎีบท
เมื่อเส้นตรงเส้นหนึ่งตัดเส้นตรงคู่หนึ่ง เส้นตรงคู่นั้นขนานกัน ก็ต่อเมื่อ มุมแย้งมีขนาดเท่ากัน
ตัวอย่างที่ 1 จงพิจารณาว่า \overleftrightarrow{AB} กับ \overleftrightarrow{CD} ขนานกันหรือไม่
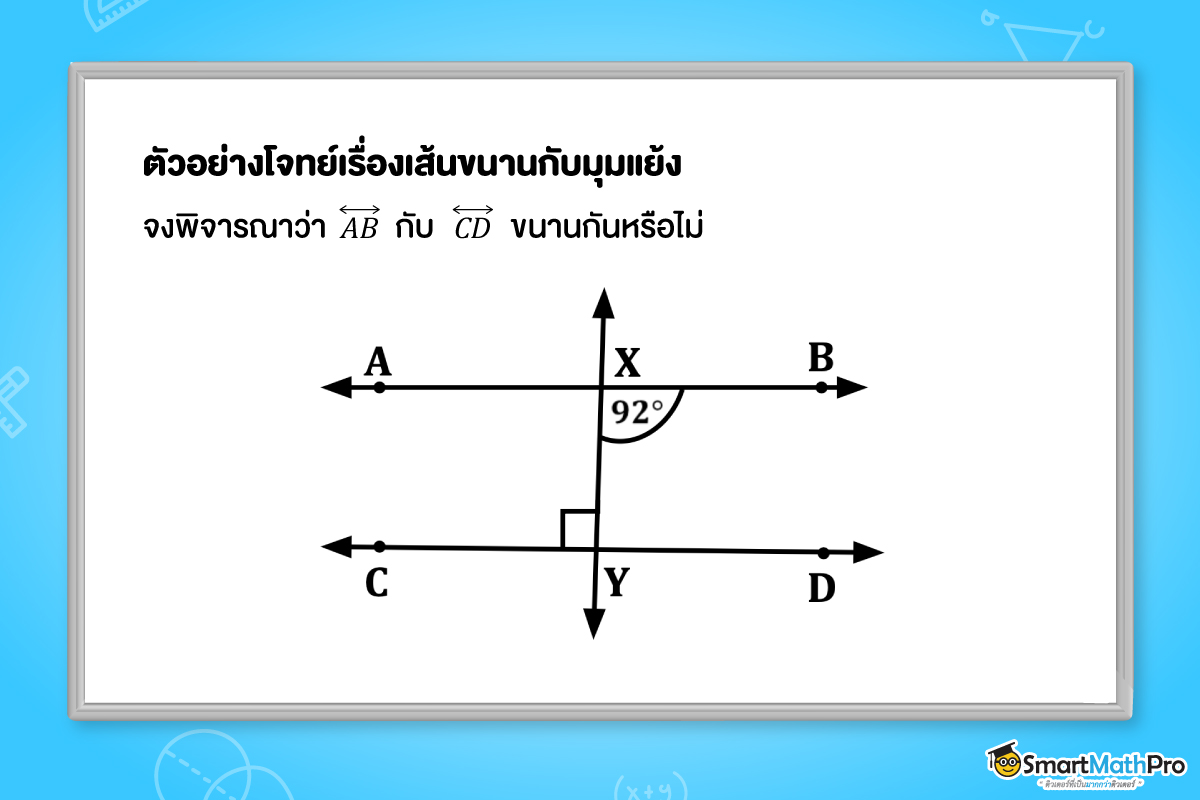
วิธีทำ จากรูป B\widehat{X}Y=92^{\circ} และ X\widehat{Y}C=90^{\circ}
ซึ่ง B\widehat{X}Y และ X\widehat{Y}C เป็นมุมแย้งกัน แต่ขนาดของทั้งสองมุมไม่เท่ากัน
ดังนั้น \overleftrightarrow{AB} กับ \overleftrightarrow{CD} ไม่ขนานกัน
ตัวอย่างที่ 2 จากรูป กำหนดให้ \overleftrightarrow{AB} // \overleftrightarrow{CD} จงหาค่าของ a
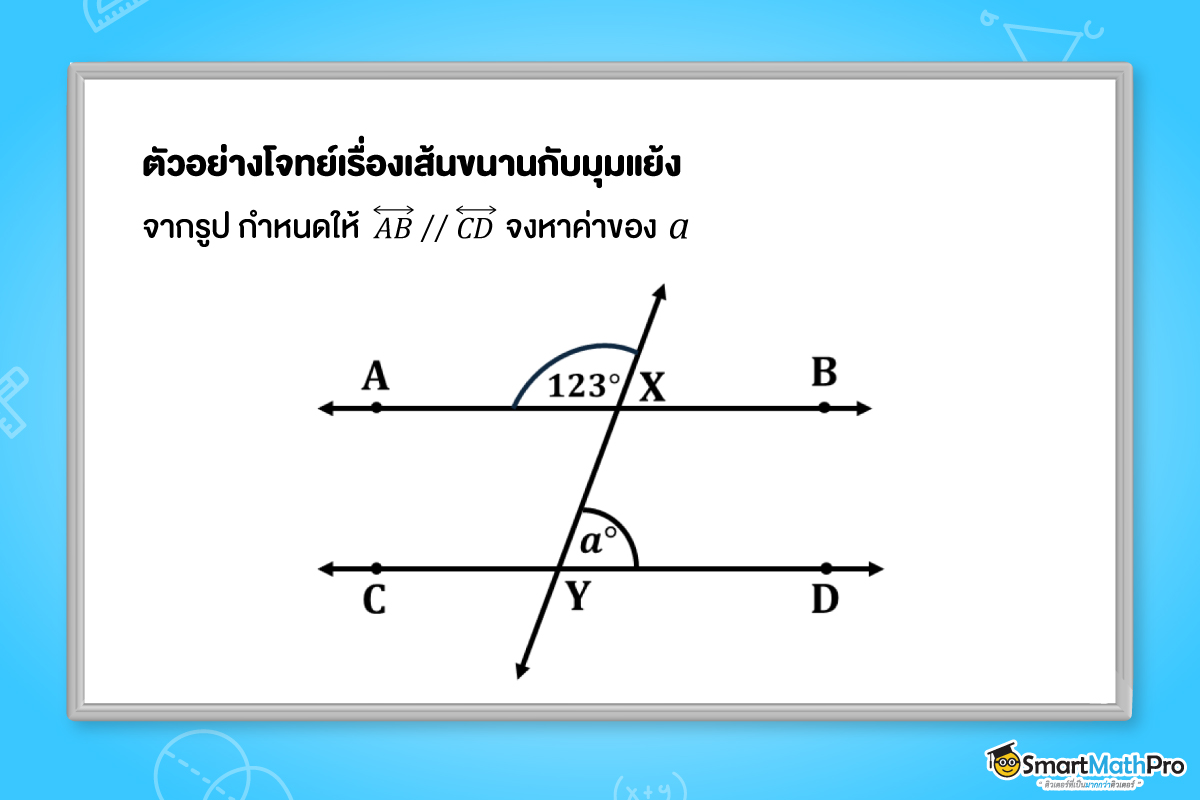
วิธีทำ จาก \overleftrightarrow{AB} // \overleftrightarrow{CD}
จะได้ A\hat{X}Y และ X\hat{Y}D เป็นมุมแย้งกัน แสดงว่ามีขนาดเท่ากัน
จาก \overleftrightarrow{XY} จะได้ว่า 123^{\circ}+A\hat{X}Y=180^{\circ}
นั่นคือ A\hat{X}Y=57^{\circ}
A\hat{X}Y = X\hat{Y}D =57^{\circ}
ดังนั้น a=57
เส้นขนานกับมุมภายในและมุมภายนอก
ทฤษฎีบท
เมื่อเส้นตรงเส้นหนึ่งตัดเส้นตรงคู่หนึ่ง เส้นตรงคู่นั้นขนานกัน ก็ต่อเมื่อ มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้าง เดียวกันของเส้นตัดมีขนาดเท่ากัน
ตัวอย่างที่ 3 จงพิจารณาว่า \overleftrightarrow{AB} กับ \overleftrightarrow{CD} ขนานกันหรือไม่
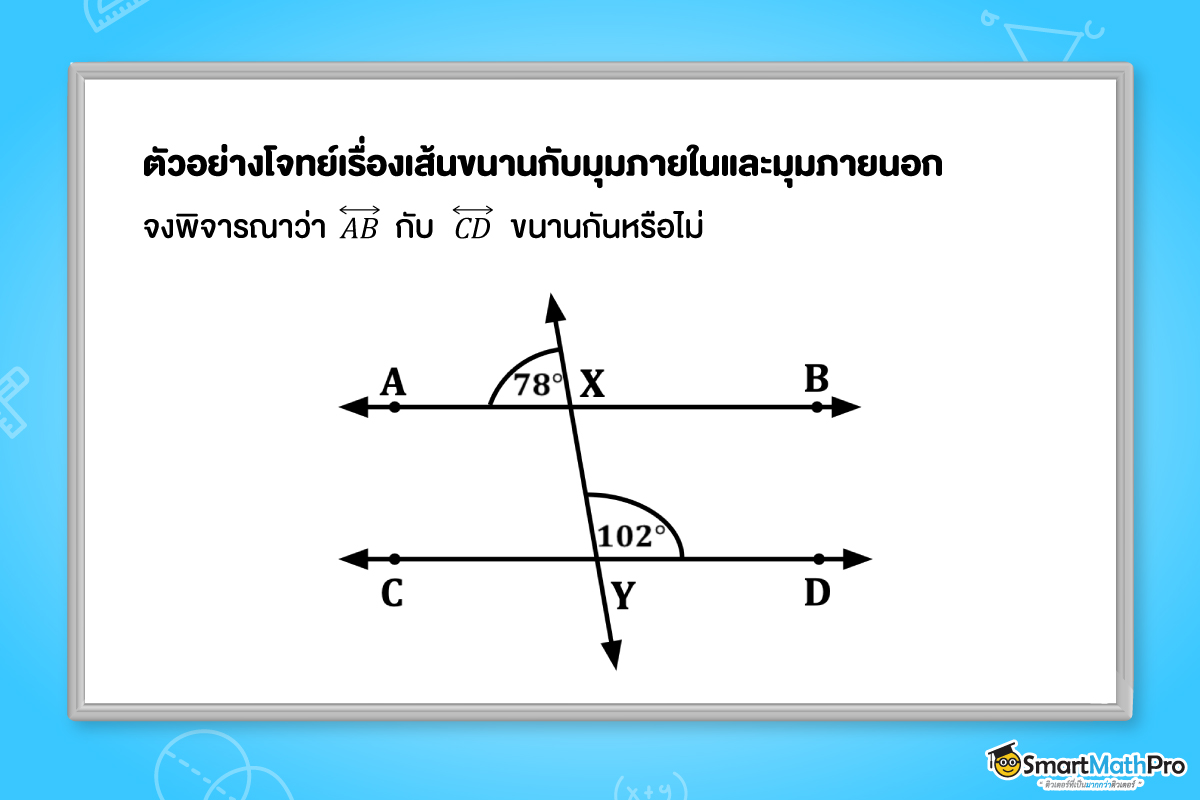
วิธีทำ จาก \overleftrightarrow{CD} จะได้ว่า C\widehat{Y}X+102^{\circ}=180^{\circ}
นั่นคือ C\widehat{Y}X=78^{\circ}
จะสังเกตได้ว่า มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัดมีขนาดเท่ากัน
ดังนั้น \overleftrightarrow{AB} กับ \overleftrightarrow{CD} ขนานกัน
ตัวอย่างที่ 4 จากรูป กำหนดให้ \overleftrightarrow{AB} // \overleftrightarrow{CD} จงหาค่าของ a
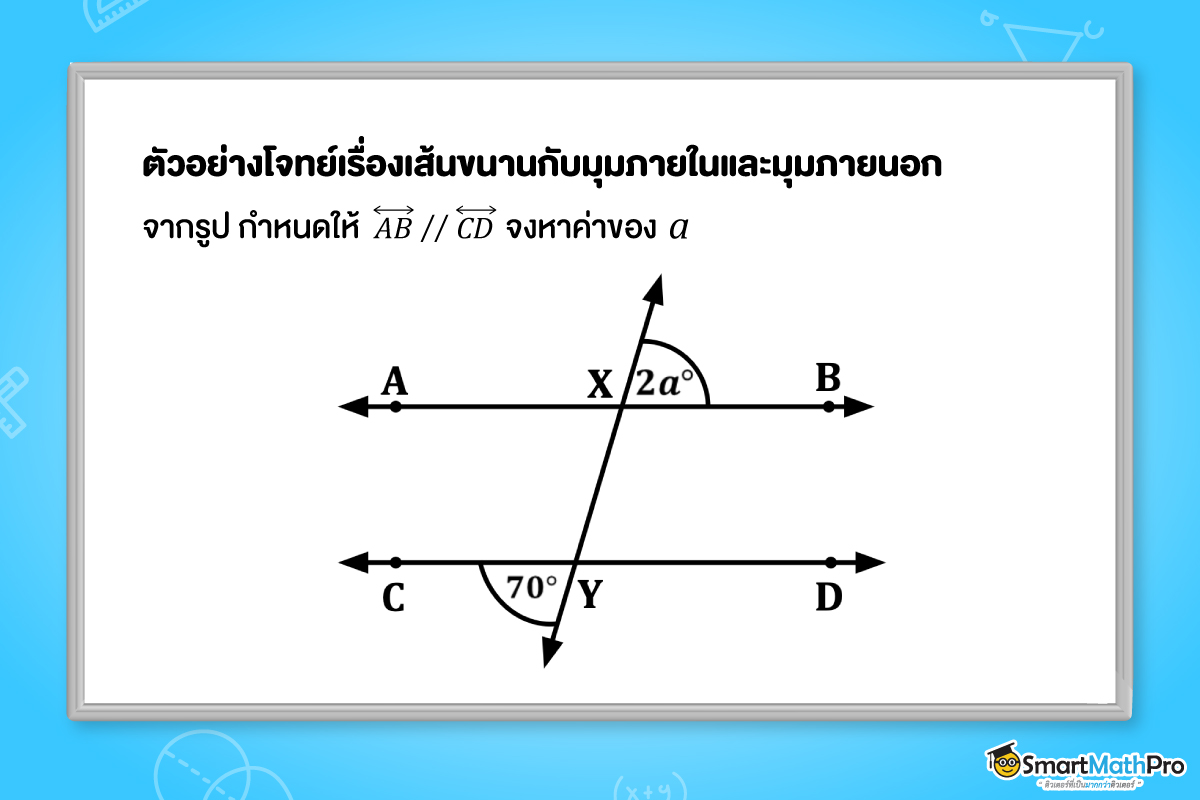
วิธีทำ จาก \overleftrightarrow{AB} // \overleftrightarrow{CD}
จะได้มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัดมีขนาดเท่ากัน
นั่นคือ X\widehat{Y}D=2a^{\circ}
จากมุมตรงข้ามกันมีขนาดเท่ากัน และ X\widehat{Y}D อยู่ตรงข้ามกับมุม 70^{\circ}
นั่นคือ X\widehat{Y}D =70^{\circ}
จะได้ว่า 2a^{\circ}=70^{\circ}
ดังนั้น a=35
เส้นขนานกับรูปสามเหล่ียม
ทฤษฎีบท
ถ้าต่อด้านใดด้านหนึ่งของรูปสามเหล่ียมออกไป แล้วมุมภายนอกที่เกิดขึ้นจะมีขนาดเท่ากับผลบวกของขนาดมุมภายในที่ ไม่ใช่มุมประชิดของมุมภายนอกนั้น
ตัวอย่างที่ 5 จากรูป จงหาค่าของ a
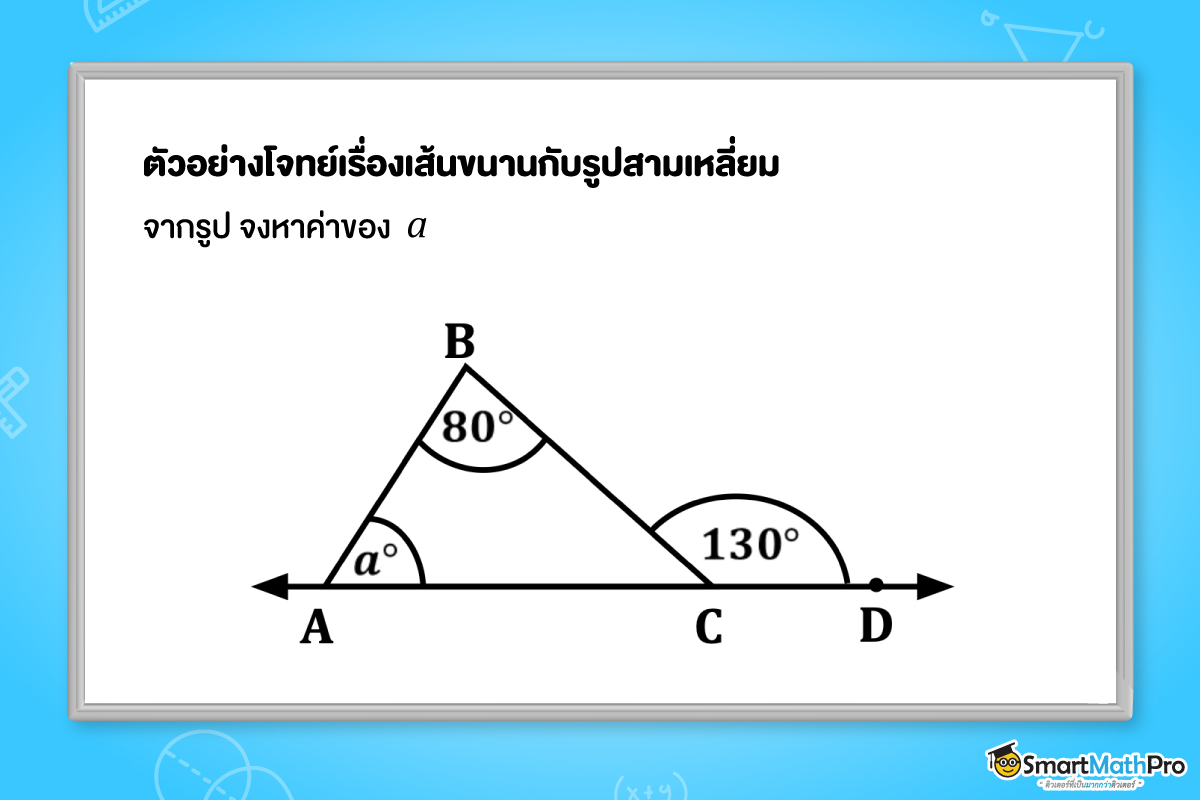
วิธีทำ จากรูป จะเห็นว่ารูปสามเหล่ียม ABC ถูกต่อ \overleftrightarrow{CD} ออกไป
นั่นคือ B\widehat{C}D=B\widehat{A}C+C\widehat{B}A
จะได้ว่า 130^{\circ}=80^{\circ}+a^{\circ}
ดังนั้น a=50
ตัวอย่างที่ 6 จากรูป กำหนดให้ \overleftrightarrow{EF} // \overleftrightarrow{CD} จงหาค่าของ a
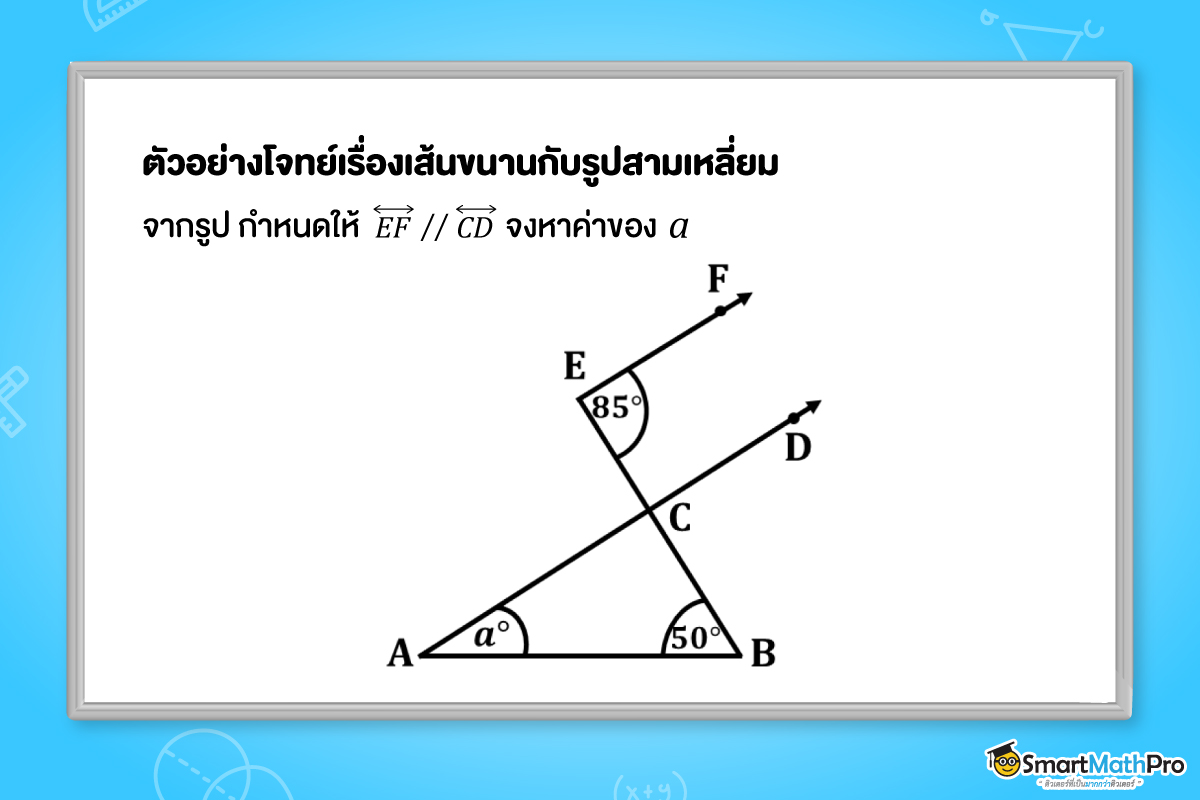
วิธีทำ จาก \overleftrightarrow{EF} // \overleftrightarrow{CD}
จะได้ว่า F\widehat{E}C=E\widehat{C}A เพราะเป็นมุมแย้งกัน
จะเห็นว่ารูปสามเหล่ียม ABC ถูกต่อ \overleftrightarrow{CE} ออกไป
นั่นคือ E\widehat{C}A=C\widehat{A}B+A\widehat{B}C
จะได้ว่า 85^{\circ}=a^{\circ}+50^{\circ}
ดังนั้น a=35
เนื้อหาของเส้นขนาน ม.2 ก็มีประมาณนี้น้าา จะเห็นว่าเรื่องนี้ไม่มีสูตรอะไรที่ให้น้อง ๆ จำเลย แต่ต้องอาศัยการเข้าใจทฤษฎีของเส้นขนาน, สมบัติและมุมต่าง ๆ ให้แม่นเป็นหลัก นอกจากนี้พี่แนะนำให้ฝึกจากการทำโจทย์ / แบบฝึกหัดเรื่องเส้นขนาน กันเยอะ ๆ เลย จะยิ่งทำให้น้อง ๆ คล่องมือกับโจทย์เรื่องนี้มากขึ้นนั่นเองง
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
คณิตศาสตร์ ม.3 เทอม 1, เทอม 2 เรียนอะไรบ้าง ? อัปเดตตาม สสวท.
สรุปพื้นฐาน ทฤษฎีบทพีทาโกรัส แบบเข้าใจง่ายพร้อมตัวอย่างโจทย์
เลขยกกำลัง คืออะไร? สรุปเนื้อหาพร้อมแจกตารางเลขยกกำลังที่ควรรู้
บทความ แนะนำ
คณิตศาสตร์ ม.2 เทอม 1, เทอม 2 เรียนอะไรบ้าง อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
