เลขยกกำลังคืออะไร ? สมบัติของเลขยกกำลัง มีอะไรบ้าง ? เราจะหาผลลัพธ์ที่อยู่ในรูปเลขยกกำลังได้อย่างไร ? น้อง ๆ คนไหนที่กำลังเรียนเรื่องนี้อยู่ หรือเรียนผ่านมาแล้วแต่ยังมีจุดที่ไม่เข้าใจ หายห่วงได้เลยย
เพราะวันนี้พี่เอาสรุปเรื่องเลขยกกำลังมาฝากเพื่อให้ทุกคนได้เข้าใจเรื่องนี้มากขึ้น ใครที่ยังไม่เข้าใจหรือมีพื้นฐานเรื่อง
เลขยกกำลังไม่แข็งแรง ก็มาทบทวนไปด้วยกันเลยน้าาา
น้อง ๆ อาจจะเคยใช้ความรู้ในการคำนวณหาค่าของเลขยกกำลัง จากการเรียนเรื่องเลขยกกำลังในระดับชั้น ม.1 หรือเคยเขียนสัญกรณ์วิทยาศาสตร์มาแล้วใช่ไหม ในหัวข้อนี้เราจะมาทบทวนความหมายของเลขยกกำลังกัน โดยในระดับม.ต้น เราจะเริ่มต้นด้วยการเรียนเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวกหรือ 0 โดยมีบทนิยาม เป็นดังนี้
บทนิยาม
เมื่อ a เป็นจำนวนใด ๆ และ n เป็นจำนวนเต็มบวก เลขยกกำลังที่มี a เป็นฐาน และ n เป็นเลขชี้กำลัง
เมื่อเขียนด้วย a^{n} มีความหมายดังนี้
a^{n}=a \times a\times a\times \cdots \times a
(มี a คูณกันอยู่ n ตัว)
a^{n} อ่านว่า “a ยกกำลัง n” หรือ “a กำลัง n ” หรือ “กำลัง n ของ a ”
เช่น
- 3^{4}=3 \times 3\times 3\times 3=81
มีฐานคือ 3 และเลขชี้กำลังคือ 4 - \left(- \frac{1}{2} \right)^{3}=\left(- \frac{1}{2} \right) \times\left(- \frac{1}{2} \right)\times \left(- \frac{1}{2} \right)=-\frac{1}{8}
มีฐานคือ – \frac{1}{2} และเลขชี้กำลังคือ 3
บทนิยาม
เมื่อ a เป็นจำนวนใด ๆ ที่ไม่เท่ากับ 0
a^{0}=1
เช่น 7^{0}=1 และ \left( -0.4 \right)^{0}=1
หมายเหตุ : เราจะไม่นิยาม 0^0 น้าา
สมบัติเลขยกกำลัง
หลังจากทบทวนความหมายของเลขยกกำลังไปแล้ว เดี๋ยวเราจะมาดูเกี่ยวกับสมบัติของเลขยกกำลังในหัวข้อนี้กันต่อเลยย
เมื่อ a เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ 0 และ n เป็นจำนวนเต็ม
a^{-n}=\frac{1}{a^{n}}
ตัวอย่างที่ 1 จงหาผลลัพธ์ 5^{-4}
วิธีทำ 5^{-4}
=\frac{1}{5^{4}}
=\frac{1}{625}
เมื่อ a เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ 0
m และ n เป็นจำนวนเต็ม
a^{m}\cdot a^{n}=a^{m+n}
ตัวอย่างที่ 2 จงหาผลคูณ 5^{-10}\times 125 ในรูปเลขยกกำลัง
วิธีทำ 5^{-10}\times 125
=5^{-10}\times 5^{3}
=5^{-10+3}
=5^{-7}
เมื่อ a เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ 0
m และ n เป็นจำนวนเต็ม
\frac{a^{m}}{a^{n}}=a^{m-n}
ตัวอย่างที่ 3 จงหาผลลัพธ์ \frac{625}{25}
วิธีทำ \frac{625}{25}
=\frac{5^{4}}{5^{2}}
=5^{4-2}
=5^{2}
=25
เมื่อ a เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ 0
m และ n เป็นจำนวนเต็ม
\left (a^{m} \right)^{n}=a^{m\cdot n}
ตัวอย่างที่ 4 จงเขียน 125^{2} ในรูปเลขยกกำลังที่มีฐานเท่ากับ 5
วิธีทำ 125^{2}
=\left ( 5^{3} \right )^{2}
=5^{3\cdot (2)}
=5^{6}
เมื่อ a เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ 0 และ n เป็นจำนวนเต็ม
\left (ab\right)^{n}=a^{n}\cdot b^{n}
ตัวอย่างที่ 5 จงเขียน 6^{4} ในรูปเลขยกกำลังที่มีฐานเท่ากับ 2 และ 3
วิธีทำ 6^{4}
=\left (2\cdot 3\right)^{4}
=2^{4}\cdot 3^{4}
เมื่อ a เป็นจำนวนเต็มใด ๆ ที่ไม่เท่ากับ 0 และ n เป็นจำนวนเต็ม
\left ( \frac{a}{b} \right )^{n}=\frac{a^{n}}{b^{n}}
ตัวอย่างที่ 6 จงเขียนผลลัพธ์ของการกระจายเลขชี้กำลัง \left ( \frac{2}{5} \right )^{3}
วิธีทำ \left ( \frac{2}{5} \right )^{3}
=\frac{2^{3}}{5^{3}}
สรุปสมบัติของเลขยยกกำลังที่ควรรู้
การหาผลลัพธ์ที่อยู่ในรูปเลขยกกำลัง
หัวข้อนี้เราจะใช้สมบัติของเลขยกกำลังในการจัดรูปเลขยกกำลังที่โจทย์กำหนดให้อยู่ในรูปอย่างง่าย
ตัวอย่างที่ 7 จงหาผลลัพธ์ของ \frac{\left( a^{-2}b^{-4}\times a^5b^2 \right)^2}{a^3b^{-1}} เมื่อ a\neq0 และ b\neq0
วิธีทำ \frac{\left( a^{-2}b^{-4}\times a^5b^2 \right)^2}{a^3b^{-1}}
=\frac{\left( a^{-2}b^{-4} \right)^2 \times \left( a^5b^2 \right)^2}{a^3b^{-1}}
=\frac{a^{\left( -2\times2 \right)}b^{\left( -4\times2 \right)}\times a^{\left( 5\times2 \right)}b^{\left( 2\times2 \right)}}{a^3b^{-1}}
=\frac{a^{-4}b^{-8}\times a^{10}b^4}{a^3b^{-1}}
=\frac{a^{\left( -4+10 \right)}b^{\left( -8+4 \right)}}{a^3b^{-1}}
=\frac{a^6b^{-4}}{a^3b^{-1}}
=a^{\left( 6-3 \right)}b^{\left( \left( -4 \right)-\left( -1 \right) \right)}
=a^3b^{-3}
=\frac{a^3}{b^3}
ตัวอย่างที่ 8 ระยะทาง 1 หน่วยดาราศาสตร์ (astronomical unit) มีค่าเท่ากับระยะทางเฉล่ียจากโลกถึงดวงอาทิตย์ ซึ่งมีค่าประมาณ 150 \times 10^6 กิโลเมตร ดาวยูเรนัสเป็นดาวเคราะห์ดวงหนึ่งในระบบสุริยะ ซึ่งมีระยะทางเฉล่ียจากดาวยูเรนัสถึงดวงอาทิตย์ประมาณ 2.9 \times10^9 กิโลเมตร จงหาระยะทางเฉล่ียที่ดาวยูเรนัสอยู่ห่างจากดวงอาทิตย์ในหน่วยดาราศาสตร์
วิธีทำ 1 หน่วยดาราศาสตร์ มีค่าประมาณ 150 \times10^6 กิโลเมตร ระยะทางเฉลี่ยจากดาวยูเรนัสถึงดวงอาทิตย์ประมาณ 2.9 \times10^9 กิโลเมตร ดังนั้น ดาวยูเรนัสอยู่ห่างจากดวงอาทิตย์ เท่ากับ \frac{2.9 \times10^9 }{150 \times10^6}=0.0193 \times10^3=19.3 หน่วยดาราศาสตร์โดยประมาณ
การนำเลขยกกำลังไปใช้
สัญกรณ์วิทยาศาสตร์
สัญกรณ์วิทยาศาสตร์ เป็นการเขียนจำนวนในรูป A \times 10^n เมื่อ 1\le A<10 และ n เป็นจำนวนเต็ม
ตัวอย่างที่ 9 จงหาผลลัพธ์ของ \frac{(0.008)^2\times \left(- \frac{1}{2} \right)^2}{\frac{1}{100}} ในรูปสัญกรณ์วิทยาศาสตร์
วิธีทำ \frac{(0.008)^2\times \left(- \frac{1}{2} \right)^2}{\frac{1}{100}}
=\left( 8\times10^{-3} \right)^2\times \frac{1}{4}\times 100
=16\times 10^{-6}\times 0.25\times 100
=16\times 10^{-6}\times25
=400\times 10^{-6}
=4\times10^{-4}
ตัวอย่างเนื้อหา ม.ปลาย ที่นำเลขยกกำลังไปใช้
เนื้อหาเลขยกกำลังในคณิตศาสตร์ ม.ปลาย มีส่วนที่เพิ่มเติมจาก ม.ต้น ตรงที่เราจะศึกษาเกี่ยวกับเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะหรือจำนวนอตรรกยะ โดยสมบัติของเลขยกกำลังก็จะคล้ายกับที่เรียนในระดับชั้น ม.ต้น เลย แต่จะมีบทนิยามที่น้อง ๆ จะได้เรียนรู้เพิ่มเติม เช่น
ให้ a เป็นจำนวนจริง และ n เป็นจำนวนเต็มที่มากกว่า 1 ถ้า a มีรากที่ n แล้ว
a^\frac{1}{n}=\sqrt[n]{a}
ตัวอย่างที่ 10 จงเขียนจำนวน \sqrt[3]{25^2} \times\sqrt[6]{25^{11}} ให้อยู่ในรูปอย่างง่าย และเลขยกกำลังทุกจำนวนมีเลขชี้กำลังเป็นจำนวนจริงบวก
วิธีทำ \sqrt[3]{25^2}\times\sqrt[6]{25^{11}}=25^\frac{2}{3}\times25^\frac{11}{6}=25^{(\frac{2}{3}+\frac{11}{6})}=\left(5^2\right)^\frac{15}{6}=5^5=3,125
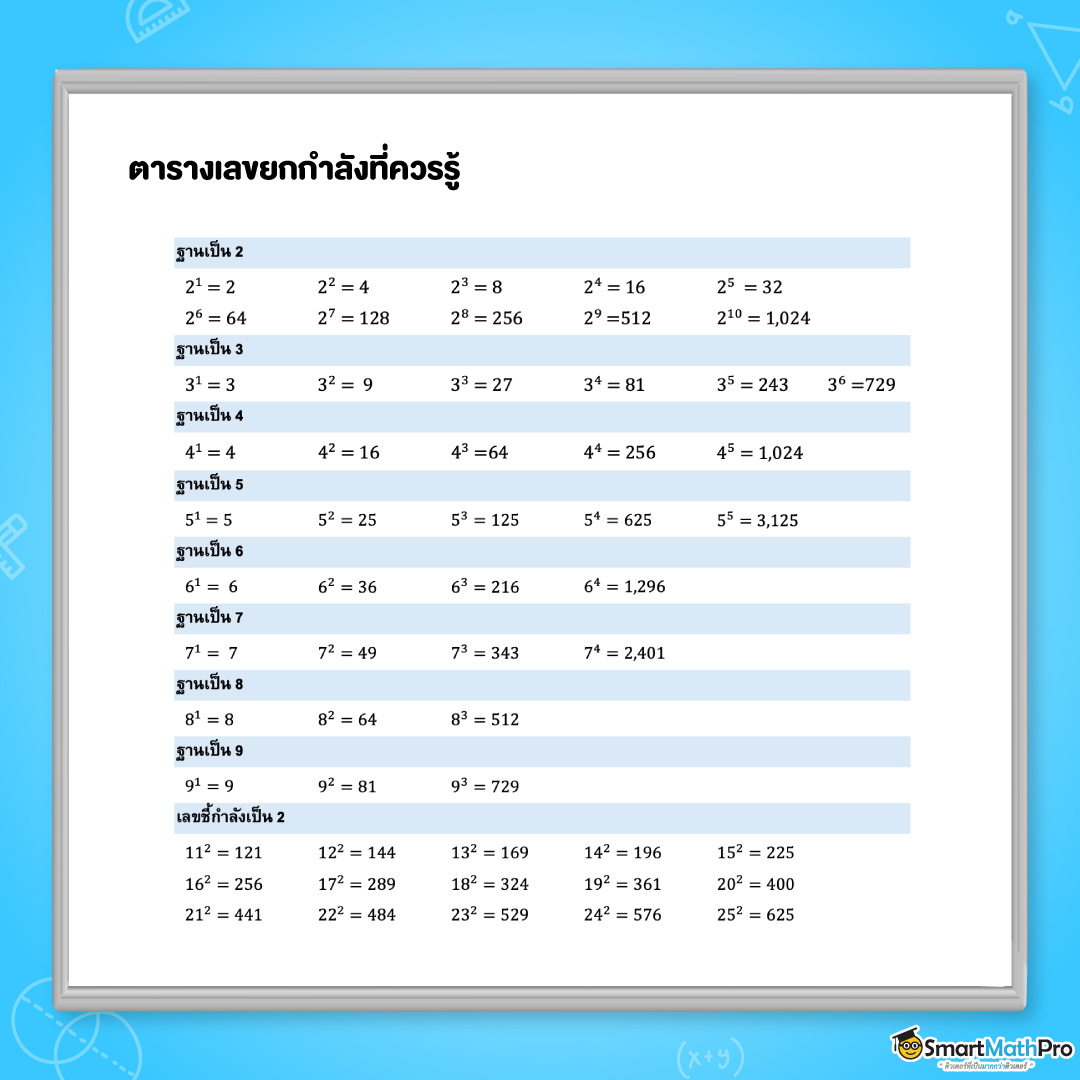
ตารางเลขยกกำลังที่ควรรู้
ดูคลิปติวเลขยกกำลัง
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
เป็นอย่างไรบ้างสำหรับสรุปเรื่องเลขยกกำลังที่พี่เอามาฝากวันนี้ หวังว่าจะทำให้น้อง ๆ เข้าใจเรื่องเลขยกกำลังมากขึ้นน้า และพี่แนะนำว่าหลังจากทบทวนจบแล้วก็อย่าลืมฝึกทำโจทย์ / แบบฝึกหัดที่มีการใช้เลขยยกกำลังเยอะ ๆ ด้วย จะช่วยให้เห็นภาพรวมเรื่องนี้มากขึ้น และสามารถนำไปปรับใช้เนื้อหาคณิต ม.ปลาย ได้อีกเยอะเลย
แต่สำหรับใครที่เรียนเนื้อหา ทบทวน และฝึกทำโจทย์ด้วยตัวเองแล้ว แต่ยังมีเนื้อหาบางจุดที่ไม่เข้าใจ อยากได้คนช่วยไกด์พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้ม
มาก เรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลยยยย
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม ม.4 สรุปเนื้อหาพร้อมตัวอย่างโจทย์
ลำดับและอนุกรม ม.6 คืออะไร สรุปเนื้อหาพร้อมตัวอย่างโจทย์และวิธีทำ
แคลคูลัส ม.6 สรุปเนื้อหา โจทย์แคลคูลัสพร้อมวิธีทำ และคลิปติวฟรี
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
Twitter : @PanSmartMathPro
Tiktok : @pan_smartmathpro
