น้อง ๆ หลายคนคงได้เรียนเรื่อง “โดเมนและเรนจ์” ในบทเรียนความสัมพันธ์และฟังก์ชันกันแล้ว แต่มีใครสงสัยไหมว่า
โดเมนและเรนจ์หาอย่างไร ? แล้วมีกี่วิธีในการหาโดเมนและเรนจ์ ?
วันนี้พี่ได้สรุปเทคนิคการหาโดเมนและเรนจ์มาให้น้อง ๆ หายสงสัย ใครที่ยังไม่เข้าใจหรืออยากได้เทคนิคเพื่อเตรียมตัวสอบ ต้องห้ามพลาด เพราะนอกจากสรุปเทคนิค พี่ยังมีตัวอย่างโจทย์พร้อมเฉลยแบบละเอียดให้ด้วย เล่ือนลงไปดูกัน !!
น้อง ๆ หลายคนที่ได้เรียนเรื่องความสัมพันธ์และฟังก์ชันน่าจะพอจำกันอยู่แล้วว่าโดเมนและเรนจ์ของความสัมพันธ์
คืออะไร ? แต่พี่ขอทบทวนบทนิยามสั้น ๆ ก่อนจะพาไปดูเทคนิคการหาโดเมนและเรนจ์นิดนึงน้าา
บทนิยาม
ให้ r เป็นความสัมพันธ์จาก A ไป B
- โดเมนของ r คือ เซตของสมาชิกตัวหน้าของคู่อันดับทั้งหมดใน r เขียนแทนด้วย D_r
- เรนจ์ของ r คือ เซตของสมาชิกตัวหลังของคู่อันดับทั้งหมดใน r เขียนแทนด้วย R_r
เทคนิคการหาโดเมนและเรนจ์โดยพิจารณาเงื่อนไข
ถ้าโจทย์กำหนดความสัมพันธ์ที่เขียนในรูปของเซตแบบบอกเงื่อนไข ให้น้อง ๆ ใช้เทคนิคในการพิจารณาเงื่อนไขแล้ว
หาโดเมนและเรนจ์ของความสัมพันธ์ ซึ่งจะมีขั้นตอนดังต่อไปนี้เลย
ขั้นตอนการหาโดเมนและเรนจ์
ขั้นตอนที่ 1 ให้น้อง ๆ จัดรูป โดย
หาโดเมน ให้เขียน y ในรูปของ x (หาโดเมน ให้ y ยืนเหงา)
หาเรนจ์ ให้เขียน x ในรูปของ y (หาเรนจ์ ให้ x ยืนเหงา)
ขั้นตอนที่ 2 ใช้ความรู้จากบทจำนวนจริงช่วยพิจารณาเงื่อนไข ซึ่งมักจะอยู่ใน 4 รูปแบบต่อไปนี้
รูปแบบที่ 1 : เศษส่วน (ตัวส่วน \neq 0)
การหาโดเมนและเรนจ์ของความสัมพันธ์ที่มีเงื่อนไขอยู่ในรูป “เศษส่วน” มักจะทำด้วยวิธีนี้
ตั้งอสมการ “ตัวส่วน \neq 0”และแก้อสมการดังกล่าว
แล้วนำค่าที่ได้ไปพิจารณาหาโดเมนและเรนจ์ต่อ
ตัวอย่างที่ 1 กำหนดให้ r=\left\{\left ( x,y \right )|y=\frac{1}{x+1} \right\} จงหาโดเมนและเรนจ์ของความสัมพันธ์นี้
- หา D_r โดยเขียน y ในรูป x (y ยืนเหงา)
พิจารณา y=\frac{1}{x+1}
เราจะเห็นว่าเงื่อนไขอยู่ในรูปเศษส่วน แสดงว่า ตัวส่วน \neq 0
จะได้ว่า x+1\neq 0
x\neq -1
ดังนั้น D_{r}=\mathbb{R}-\left\{-1 \right\} - หา R_r โดยเขียน x ในรูป y (x ยืนเหงา)
จาก y=\frac{1}{x+1}
จัดรูปใหม่จะได้ x=\frac{1}{y}-1
จะเห็นว่าเงื่อนไขอยู่ในรูปเศษส่วน แสดงว่า ตัวส่วน \neq 0
จะได้ว่า y\neq 0
ดังนั้น R_{r}=\mathbb{R}-\left\{0 \right\}
รูปแบบที่ 2 : กรณฑ์ที่สอง
การหาโดเมนและเรนจ์ของความสัมพันธ์ที่มีเงื่อนไขอยู่ในรูป “กรณฑ์ที่สอง” มักจะทำด้วยวิธีนี้
ตั้งอสมการ “ก้อนข้างในกรณฑ์ที่ 2 \geq 0”
และ “อีกฝั่งของก้อนกรณฑ์ที่สอง \geq 0” จากนั้นแก้อสมการดังกล่าว
แล้วนำค่าที่ได้ไปพิจารณาหาโดเมนและเรนจ์ต่อ
ตัวอย่างที่ 2 กำหนดให้ r=\left\{ (x,y)|y=\sqrt{x-2} \right\} จงหาโดเมนและเรนจ์ของความสัมพันธ์นี้
- หา D_r โดยเขียน y ในรูป x (y ยืนเหงา)
พิจารณา y=\sqrt{x-2}
จะเห็นว่าเงื่อนไขอยู่ในรูปกรณฑ์ที่สอง แสดงว่า ตัวในรูท \geq 0
จะได้
x-2\ge 0 \\ x\ge 2
ดังนั้น D_{r}=[2,\infty ) - หา R_r โดยเขียน x ในรูป y (x ยืนเหงา)
พิจารณา y=\sqrt{x-2}
จะเห็นว่าเงื่อนไขอยู่ในรูปกรณฑ์ที่สอง แสดงว่า ก้อนข้างในรูท \geq 0
แสดงค่าของรูท \geq 0
จะได้ว่า \sqrt{x-2}\ge 0\\ y\ge 0
ดังนั้น R_{r}=[0,\infty )
รูปแบบที่ 3 : ยกกำลังด้วยจำนวนคู่
การหาโดเมนและเรนจ์ของความสัมพันธ์ที่มีเงื่อนไขอยู่ในรูป “ยกกำลังด้วยจำนวนคู่” มักจะทำด้วยวิธีนี้
ตั้งอสมการ “อีกฝั่งของก้อนที่ยกกำลังด้วยจำนวนคู่ \geq 0”
จากนั้นแก้อสมการดังกล่าว แล้วนำค่าที่ได้ไปพิจารณาหาโดเมนและเรนจ์ต่อ
ตัวอย่างที่ 3 กำหนดให้ r=\left\{(x,y)|y=x^{2}+3 \right\} จงหาโดเมนและเรนจ์ของความสัมพันธ์นี้
- หา D_r โดยเขียน y ในรูป x (y ยืนเหงา)
พิจารณา y=x^{2}+3
จะเห็นว่าเงื่อนไขอยู่ในรูปยกกำลังด้วยจำนวนคู่
แสดงว่าตัวที่ถูกยกกำลังด้วยจำนวนคู่ พิจารณาตามเงื่อนไขของตัวนั้นได้เลย
จะได้ว่า x ไม่มีเงื่อนไขใด
ดังนั้น D_{r}=\mathbb{R} - หา R_r โดยเขียน x ในรูป y (x ยืนเหงา)
พิจารณา y=x^{2}+3
จะเห็นว่าเงื่อนไขอยู่ในรูปยกกำลังด้วยจำนวนคู่ แสดงว่าก้อนที่ยกกำลังด้วยจำนวนคู่ \geq 0
จะได้ว่า
x^{2}\ge 0\\ x^{2}+3\ge 3\\ y\ge 3
ดังนั้น R_{r}=[3,\infty )
รูปแบบที่ 4 : ค่าสัมบูรณ์
การหาโดเมนและเรนจ์ของความสัมพันธ์ที่มีเงื่อนไขอยู่ในรูป “ค่าสัมบูรณ์” มักจะทำด้วยวิธีนี้
ตั้งอสมการ “อีกฝั่งของค่าสัมบูรณ์ที่ถอดค่าสัมบูรณ์ออกมาแล้วต้อง \geq 0”
จากนั้นแก้อสมการดังกล่าว แล้วนำค่าที่ได้ไปพิจารณาหาโดเมนและเรนจ์ต่อ
ตัวอย่างที่ 4 กำหนดให้ r=\left\{ \left( x, y \right)|y=\left| x+3 \right| \right\} จงหาโดเมนและเรนจ์ของความสัมพันธ์นี้
- หา D_r โดยเขียน y ในรูป x (y ยืนเหงา)
พิจารณา y=\left| x+3 \right|
จะเห็นว่า เงื่อนไขอยู่ในรูปค่าสัมบูรณ์
แสดงว่า ก้อนในค่าสัมบูรณ์ พิจารณาตามเงื่อนไข
จะได้ว่า x+3 ไม่มีเงื่อนไขใด
ดังนั้น D_r=\mathbb{R} - หา R_r โดยเขียน x ในรูป y (x ยืนเหงา)
พิจารณา y=\left| x+3 \right|
จะเห็นว่า เงื่อนไขอยู่ในรูปค่าสัมบูรณ์
แสดงว่า ค่าสัมบูรณ์มากกว่าหรือเท่ากับศูนย์
จะได้ว่า \left| x+3 \right| \geq 0 \\ y\geq 0
ดังนั้น R_r=\left [ 0, \infty \right )
จากเทคนิคการหาโดเมนและเรนจ์ของความสัมพันธ์ทั้ง 4 รูปแบบ เราสามารถสรุปให้เข้าใจง่าย ๆ ได้ด้วยภาพนี้เลย
เทคนิคการหาโดเมนและเรนจ์โดยพิจารณาจากกราฟ
ซึ่งนอกจากจะใช้การจัดรูปหรือเทคนิคเพื่อหาโดเมนและเรนจ์ได้แล้ว เราก็ยังสามารถพิจารณาจากกราฟได้เช่นเดียวกัน
ตัวอย่างที่ 5 จากกราฟของความสัมพันธ์ที่กำหนดให้ จงหาโดเมนและเรนจ์
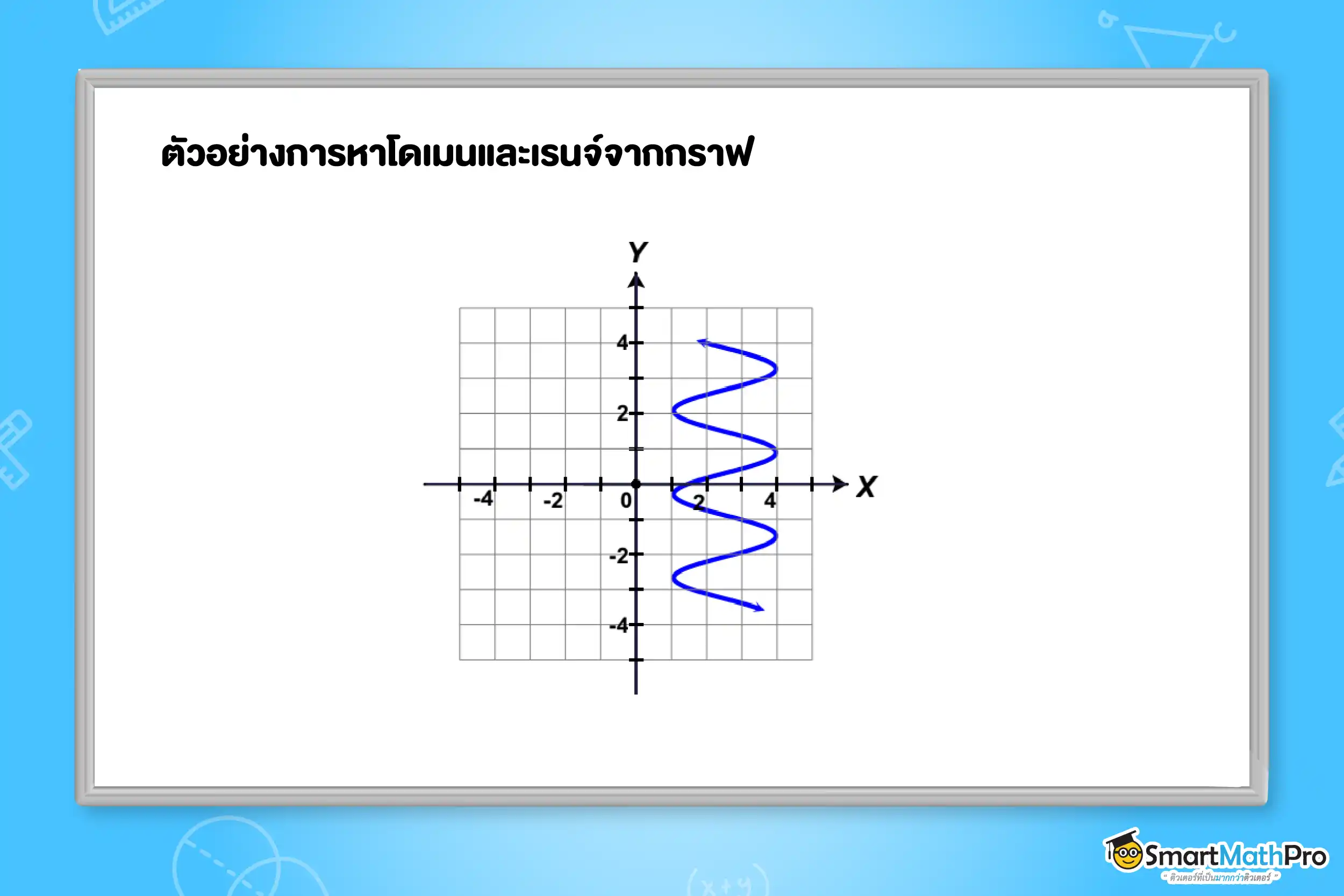
พิจารณาแนวนอน จากกราฟจะเห็นว่าค่า x อยู่ในช่วง \left [ 1, 4 \right ]
พิจารณาแนวตั้ง จากกราฟจะเห็นว่าค่า y สามารถเป็นได้ทุกค่า
ดังนั้น D_r=\left [ 1, 4 \right ] และ R_r=\mathbb{R}
ตัวอย่างที่ 6 จากกราฟของความสัมพันธ์ที่กำหนดให้ จงหาโดเมนและเรนจ์
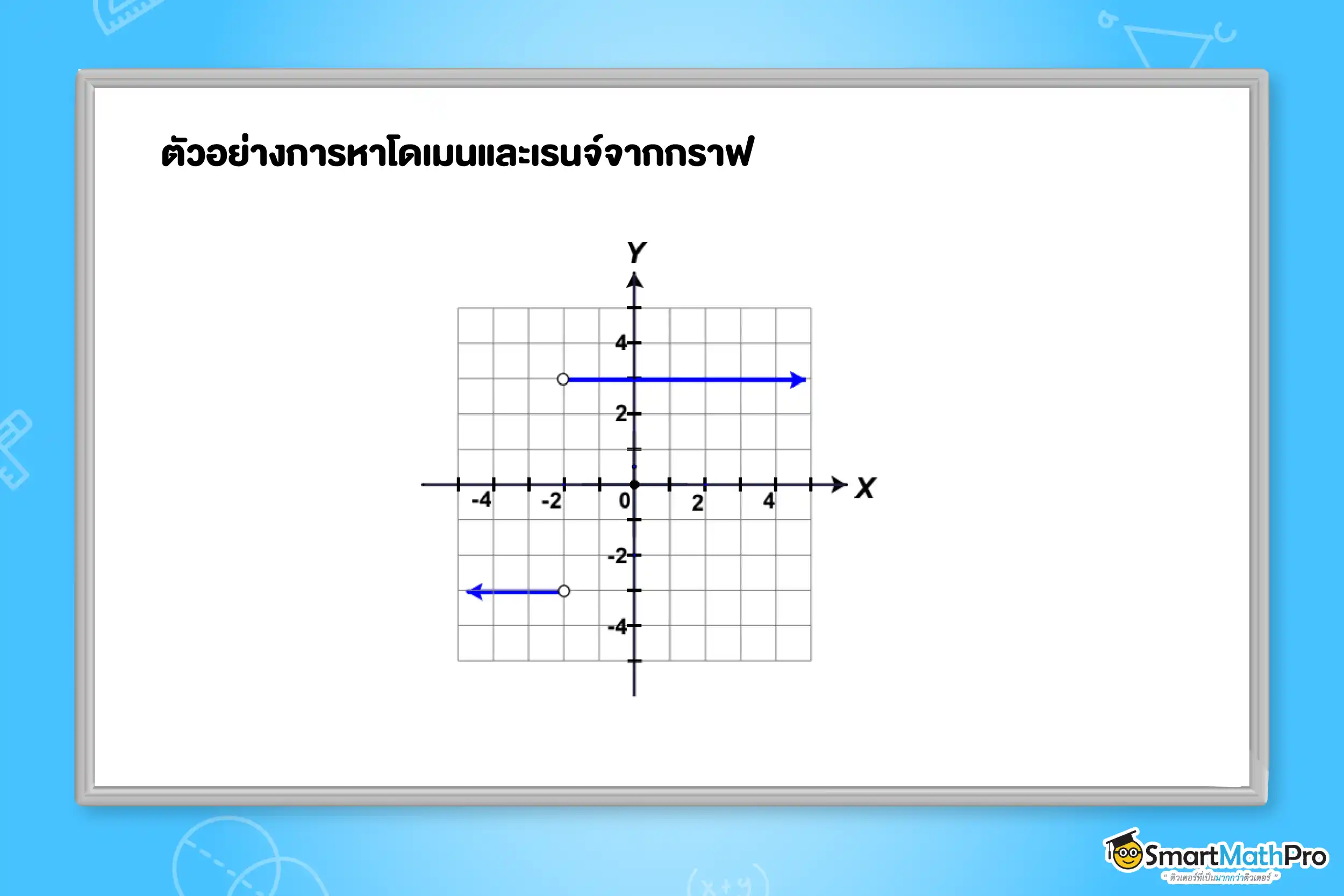
พิจารณาแนวนอน จากกราฟจะเห็นว่าค่า x สามารถเป็นได้ทุกค่า ยกเว้นที่ x=-2
พิจารณาแนวตั้ง จากกราฟจะเห็นว่าค่า y มี 2 ค่า คือที่ y= -3 และ y= 3
ดังนั้น D_r=\mathbb{R}-\left\{2 \right\} และR_r=\left\{-3, 3 \right\}
เป็นอย่างไรกันบ้างกับ “สรุปเทคนิคการหาโดเมนและเรนจ์ ม.4” ที่พี่สรุปมาให้น้อง ๆ อ่านกันในวันนี้ หวังว่าจะช่วยทุกคนที่กำลังเตรียมตัวสอบให้เก็บคะแนนปัง ๆ ได้เลยน้าา แต่ถ้าใครยังรู้สึกว่าไม่คล่อง พี่แนะนำให้ทบทวนเนื้อหาเรื่องนี้และฝึกทำโจทย์เยอะ ๆ เพราะการทำโจทย์จะช่วยให้รู้ว่าน้อง ๆ ยังไม่แม่นตรงจุดไหนบ้าง
หรือถ้าน้อง ๆ รู้สึกว่าเนื้อหาคณิตศาสตร์ ม.ปลายดูเป็นเรื่องยาก กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากเสริมพื้นฐานให้แน่นและอยากได้คนช่วยไกด์ พี่ก็ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย !!
บทความ แนะนำ
ความสัมพันธ์และฟังก์ชัน ม.4 สรุปเนื้อหาพร้อมแจกโจทย์ให้ฝึกทำ !
เซต (Set) คืออะไร สรุปเนื้อหาเซต ม.4 พร้อมโจทย์และเฉลย
จำนวนจริง ม.4 สรุปครบม้วนเดียวจบ พร้อมแจกโจทย์จำนวนจริงและวิธีทำ
ตรรกศาสตร์ ม.4 สรุปครบทุกเนื้อหาพร้อมโจทย์ตรรกศาสตร์และวิธีทำ - SmartMathPro
ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม ม.4 สรุปเนื้อหาพร้อมตัวอย่างโจทย์
เรขาคณิตวิเคราะห์ และภาคตัดกรวย ม.4 สรุปเนื้อหาพร้อมตัวอย่างโจทย์
คณิตศาสตร์ ม.4 เทอม 1,2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม
บทความ แนะนำ
ความสัมพันธ์และฟังก์ชัน ม.4 สรุปเนื้อหาพร้อมแจกโจทย์ให้ฝึกทำ !
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
Twitter : @PanSmartMathPro
Tiktok : @pan_smartmathpro
