เนื้อหา เสียง ฟิสิกส์ ม.5 มีส่วนไหนบ้างที่ควรเน้นอ่านเพื่อเตรียมสอบ A-Level ? แล้วมีสูตรไหนที่ควรรู้ ? น้อง ๆ คนไหนที่กำลังต้องการทบทวนเนื้อหาชั้น ม.5 หรือเตรียมตัวสอบ A-Level ฟิสิกส์ ต้องอ่านบทความนี้เลยยย
เพราะวันนี้พี่จะพาน้อง ๆ มาทำความเข้าใจในเรื่อง เสียง ตั้งแต่สรุปเนื้อหาสำคัญ ทบทวนสูตรต่าง ๆ ที่จำเป็น พร้อมตัวอย่างข้อสอบมาให้ดูกันด้วย อย่ารอช้า เล่ือนลงไปอ่านกันเลยดีกว่า !!
คล่ืนเสียง (sound wave)
คล่ืนเสียง (sound wave) เป็นคล่ืนกลและคล่ืนตามยาว ซึ่งเกิดจากการถ่ายทอดพลังงานจากการสั่นสะเทือนของแหล่งกำเนิดเสียงผ่านโมเลกุลของตัวกลาง (ส่วนใหญ่คืออากาศ) ไปยังผู้รับ
เมื่อคล่ืนเสียงเดินทางมาถึงหูของเรา อวัยวะรับเสียงอันซับซ้อนของเราจะทำหน้าที่รับการสั่นสะเทือนนั้น และแปลงให้เป็นสัญญาณไฟฟ้า ก่อนส่งต่อไปยังสมองเพื่อประมวลผล จนในที่สุดเราก็สามารถรับรู้และเข้าใจเสียงต่าง ๆ ที่ได้ยินได้
อัตราเร็วเสียง
อัตราเร็วเสียง หาได้จาก v=\frac{s}{t} หรือ v=f\lambda
เมื่อ v คือ อัตราเร็วเสียง มีหน่วยเป็น เมตรต่อวินาที \left ( m/s\right )
s คือ ระยะทางที่เสียงเคล่ือนที่ได้ มีหน่วยเป็น เมตร \left ( m\right )
t คือ เวลา มีหน่วยเป็น วินาที \left (s\right )
f คือ ความถี่เสียง มีหน่วยเป็น เฮิรตซ์ \left (Hz\right )
\lambda คือ ความยาวคล่ืน มีหน่วยเป็น เมตร \left ( m\right )
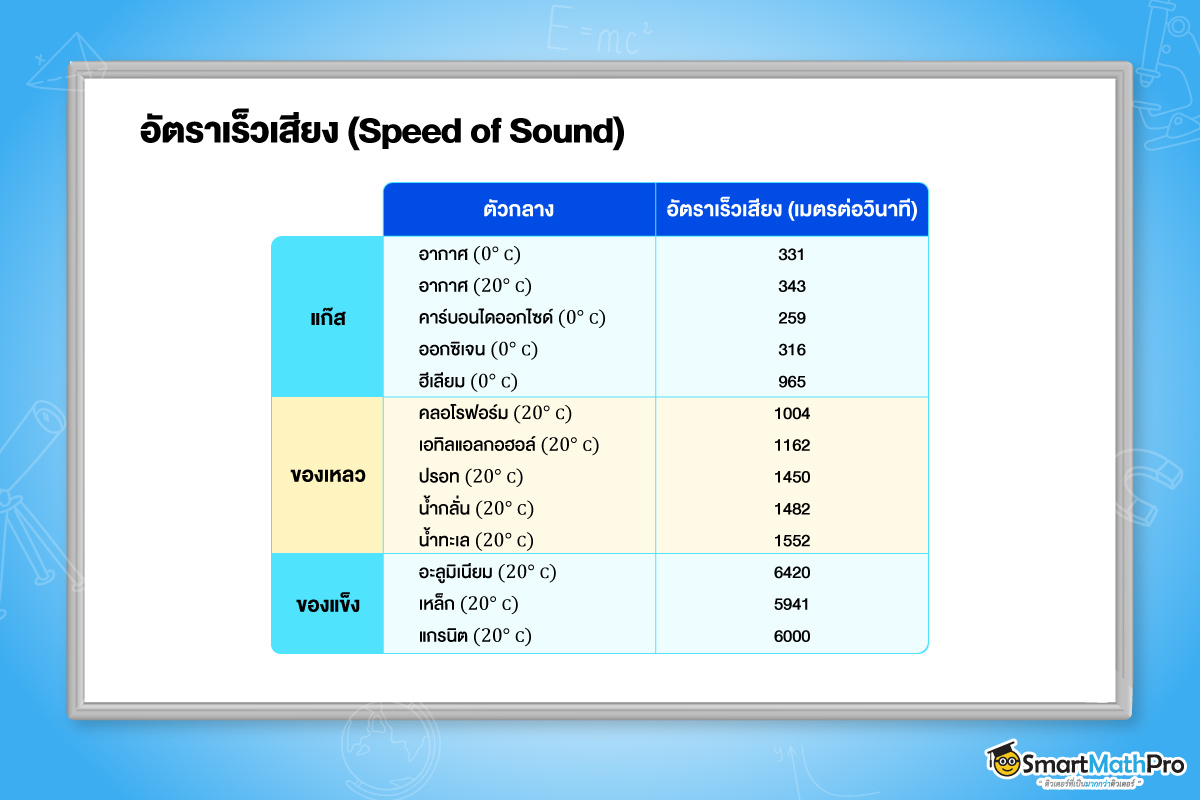
ในการเดินทางของคล่ืนเสียง อัตราเร็วของเสียงไม่ได้มีค่าคงที่เสมอไป แต่แปรผันตามปัจจัยสำคัญสองประการ คือ คุณสมบัติของตัวกลางและอุณหภูมิของสิ่งแวดล้อม
ตัวอย่างที่ 1
หากมองเห็นฟ้าแลบและได้ยินเสียงฟ้าร้องหลังจากนั้น 5 วินาที จงคำนวณว่า ตำแหน่งที่เกิดฟ้าแลบอยู่ห่างจากจุดที่สังเกตกี่เมตร กำหนดให้อุณหภูมิของอากาศขณะนั้นเป็น 25 องศาเซลเซียส
วิธีทำ:
1. คำนวณอัตราเร็วของเสียงในอากาศที่อุณหภูมิ 25°C
v=331+0.6t_{c}=331+\left ( 0.6\times 25 \right )=331+15=346 เมตรต่อวินาที
2. หาตำแหน่งที่เกิดฟ้าแลบ
s=vt=346\times 5=1,730 เมตร
ตอบ ตำแหน่งที่เกิดฟ้าแลบอยู่ห่างจากจุดที่สังเกต 1,730 เมตร
พฤติกรรมของเสียง
- เสียงที่ไปกระทบกับวัตถุแล้วสะท้อนกลับมาใช้เวลามากกว่า 0.1 วินาที ซึ่งภายในเวลาดังกล่าว หูของเราสามารถแยกเสียงทั้งสองออกจากกันได้อย่างชัดเจน ทำให้เกิดการได้ยินเสียงครั้งต่อไปได้ เรียกว่า เสียงสะท้อนกลับ (echo)
- เสียงที่ไปกระทบกับวัตถุแล้วสะท้อนกลับมาใช้เวลาน้อยกว่า 0.1 วินาที หูจะไม่สามารถแยกเสียงทั้งสองครั้งได้ เสียงที่ได้ยิน เรียกว่า การกังวาน (reverberation)
การได้ยินเสียง
ความเข้มเสียง (Sound Intensity)
ความเข้มเสียง (Sound Intensity) หมายถึง พลังงานเสียงที่ตกกระทบต่อพื้นที่ตั้งฉาก 1 ตารางหน่วย ในเวลา 1 วินาที แทนด้วยสัญลักษณ์ I
คำนวณได้จากสมการ
I=\frac{P}{A}=\frac{P}{4\pi r^{2}}
เมื่อ I คือ ความเข้มเสียง มีหน่วยเป็น วัตต์ต่อตารางเมตร (W/m^{2})
P คือ กำลังเสียง มีหน่วยเป็น วัตต์ (W)
A คือ พื้นที่ที่เสียงเคล่ือนที่ผ่านในทิศตั้งฉาก มีหน่วยเป็น ตารางเมตร (m^{2})
r คือ รัศมีวงกลม มีหน่วยเป็น เมตร \left (m\right )
ข้อควรรู้
- ความเข้มเสียงต่ำสุดที่หูมนุษย์สามารถได้ยิน (เสียงเบา) คือ I_{0}=10^{-12}W/m^{2}
- ความเข้มเสียงสูงสุดที่หูมนุษย์สามารถทนฟังได้ (เสียงดัง) คือ I_{max}=1W/m^{2}
- ความเข้มเสียงสูงสุดมีค่า 10^{12} เท่าของความเข้มเสียงต่ำสุด
ความแตกต่างระหว่างความเข้มเสียงทั้งสองนั้นกว้างมาก เพื่อเป็นการลดช่วงที่กว้างนี้ลง จึงพิจารณาการได้ยินจาก “ระดับเสียง” แทน
ระดับเสียง
ระดับเสียง (Sound Level) เป็นปริมาณที่บอกความดังของเสียง แทนด้วยสัญลักษณ์ \beta คำนวณได้จากสมการ
\beta =10log\frac{I}{I_{0}}
โดย \beta คือ ระดับเสียง มีหน่วยเป็น เดซิเบล (dB)
I คือ ความเข้มเสียงที่พิจารณา มีหน่วยเป็น วัตต์ต่อตารางเมตร (W/m^{2})
I_{0} คือ ความเข้มเสียงอ้างอิง มีค่าเท่ากับ 1\times 10^{-12} วัตต์ต่อตารางเมตร
ตัวอย่างที่ 2
วิทยุเครื่องหนึ่งกำลังส่งเสียงเพลงภายในห้อง หากผู้ฟังยืนอยู่ห่างจากวิทยุเป็นระยะทาง 1 เมตร จงคำนวณระดับเสียง
ณ ตำแหน่งดังกล่าว โดยกำหนดให้กำลังเสียงของวิทยุเท่ากับ 4\pi \times 10^{-3} วัตต์
วิธีทำ:
1. คำนวณความเข้มเสียง (I)
I=\frac{P}{A}=\frac{4\pi \times 10^{-3}}{4\pi (1)^{2}}=1\times 10^{-3}W/m^{2}
2. คำนวณระดับเสียง (\beta)
\beta =10log\frac{I}{I_{0}}=10log\frac{1\times 10^{-3}}{1\times 10^{-12}}=10log10^{9}=9\times 10log10=9\times 10=90dB
ตอบ ระดับเสียงที่ตำแหน่งห่างจากวิทยุ 1 เมตร เท่ากับ 90 เดซิเบล (dB)
ปรากฏการณ์เกี่ยวกับเสียง
คล่ืนนิ่งของเสียง
โดย จุดบัพ (Node) เป็นตำแหน่งเสียงค่อยและจุดปฏิบัพ (Antinode) เป็นตำแหน่งเสียงดัง
การสั่นพ้องของอากาศในท่อ
โดยการศึกษาเรื่องคล่ืนนิ่งของเสียง นิยมใช้ท่อปลายปิดและท่อปลายเปิด จะได้ความสัมพันธ์ ดังนี้
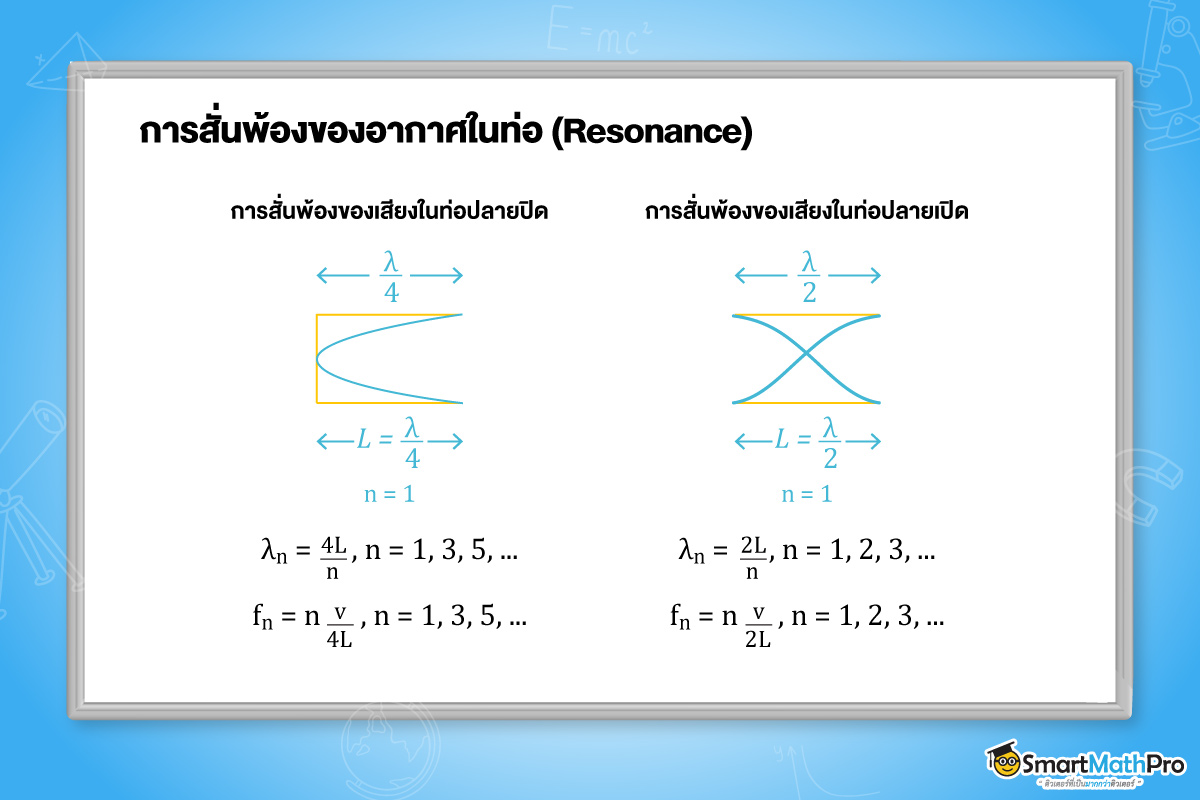
โดย f_{n} คือ ความถี่การสั่นพ้องซึ่งมีค่าเป็น n เท่าของความถี่มูลฐาน (Hz)
v คือ อัตราเร็วเสียงในอากาศ (m/s)
L คือ ความยาวของลำอากาศในท่อ(m)
ข้อควรรู้
- สำหรับการสั่นพ้องของเสียงในหลอดเรโซแนนซ์ซึ่งปรับความยาวได้ การสั่นพ้องจะเกิดขึ้นทุกระยะ \frac{\lambda }{2}
คำศัพท์ของความถี่
ความถี่มูลฐาน (Fundamental Frequency) คือ ความถี่ต่ำสุดของคล่ืนนิ่ง
โอเวอร์โทน (Overtone) คือ ความถี่ถัดจากความถี่มูลฐาน
ฮาร์มอนิก (Harmonic) คือ ตัวเลขที่บอกว่าความถี่นั้นเป็นกี่เท่าของความถี่มูลฐาน (ตัว n ในสูตร)
ตัวอย่างที่ 3 ท่อปลายปิดหนึ่งด้านมีความยาว 1 เมตร ถ้าความเร็วของเสียงในอากาศมีค่าเท่ากับ
340 เมตรต่อวินาที ความถี่มูลฐานมีค่าเท่าใด
วิธีทำ:
ความถี่มูลฐาน คือ f_{1} จะได้ว่า f_{n}=n\frac{v}{4L}
f_{n}=n\frac{v}{4L}
f_{1}=85Hz
ตอบ ความถี่มูลฐานเท่ากับ 85Hz
บีต
บีต (beat) เกิดขึ้นเมื่อมีเสียง 2 เสียงที่แอมพลิจูดเท่ากัน มีความถี่ใกล้ ๆ กันมาเจอกัน เหมือนคล่ืนสองลูกมาซ้อนทับกัน ผลที่ได้คือจะเกิดเสียงดัง – เบาสลับกันเป็นจังหวะ ซึ่งหาได้จาก
f_{b}=\left | f_{1}-f_{2}\right |
**หูของเราสามารถแยกความถี่บีตได้มากที่สุด 7Hz ถ้ามากกว่านี้จะแยกไม่ออก
โดย f_{b} คือ ความถี่บีต (Hz)
f_{1}คือ ความถี่เสียงจากแหล่งที่ 1 (Hz)
f_{2} คือ ความถี่เสียงจากแหล่งที่ 2 (Hz)
ตัวอย่างที่ 4
ถ้าเสียงแรกมีความถี่ 440Hz อีกเสียงมีความถี่ 442Hz แล้วความถี่บีตมีค่าเท่าใด
f_{b}=\left | f_{1}-f_{2}\right |
f_{b}=\left | 440-442\right |
f_{b}=2Hz
ตอบ จะได้ยินเสียงดัง – เบา 2 ครั้งต่อวินาที
เรื่องนี้มีประโยชน์มาก ๆ เลยเพราะช่างดนตรีใช้การฟังบีตเพื่อตั้งเสียงเครื่องดนตรีให้ตรงมาตรฐาน
ปรากฎการณ์ดอปเพลอร์
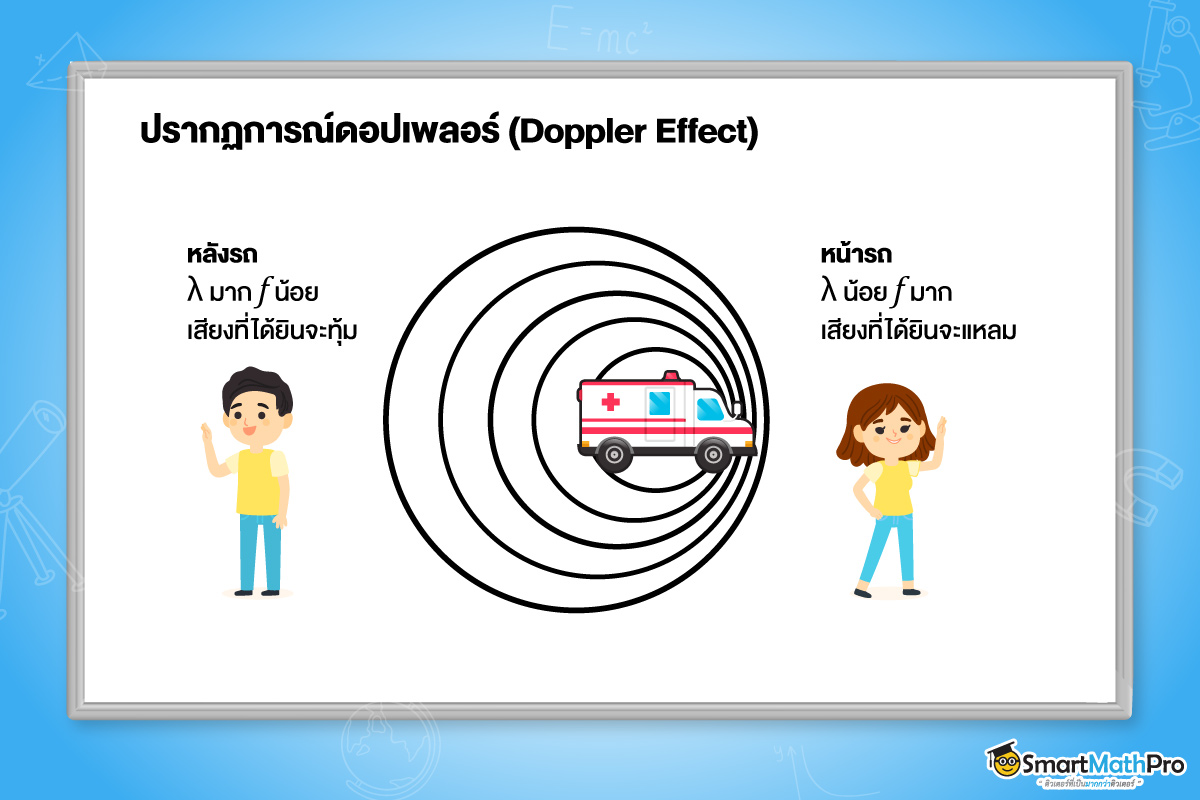
- เมื่อแหล่งกำเนิดคล่ืนเคล่ือนที่เข้าหาผู้สังเกต ความถี่ของคล่ืนที่ผู้สังเกตได้รับจะเพิ่มขึ้น (แหล่งกำเนิดคล่ืนเรียกว่า “เข้ามา” หาผู้สังเกต)
- เมื่อแหล่งกำเนิดคล่ืนเคล่ือนที่ออกห่างจากผู้สังเกต ความถี่ของคล่ืนที่ผู้สังเกตได้รับจะลดลง (แหล่งกำเนิดคล่ืนเรียกว่า “ออกไป” จากผู้สังเกต)
ตัวอย่างข้อสอบ A-Level เรื่องเสียง ฟิสิกส์
- การสั่นพ้อง (Resonance) : มักมาในรูปของโจทย์เกี่ยวกับคล่ืนนิ่งในท่อปลายเปิด – ปลายปิด หรือในเครื่องดนตรี เช่น การหาความยาวคล่ืนจากการสั่นพ้อง
- ความเข้มเสียงและระดับเสียง : มักมาในรูปของโจทย์เกี่ยวกับการคำนวณระดับเสียงเดซิเบล (dB) และการเปรียบเทียบความเข้มเสียง
- เรื่องอื่น ๆ ที่เกี่ยวกับปรากฏการณ์ทางเสียง เช่น ความถี่บีต (Beat Frequency) และการสะท้อนของเสียง
ตอบ 3. 500 Hz
ความสัมพันธ์ระหว่างสองตำแหน่งของน้ำ ตำแหน่งที่เกิดการสั่นพ้องมีจำนวนฮาร์มอนิกต่างกันอยู่ 2 ฮาร์มอนิก
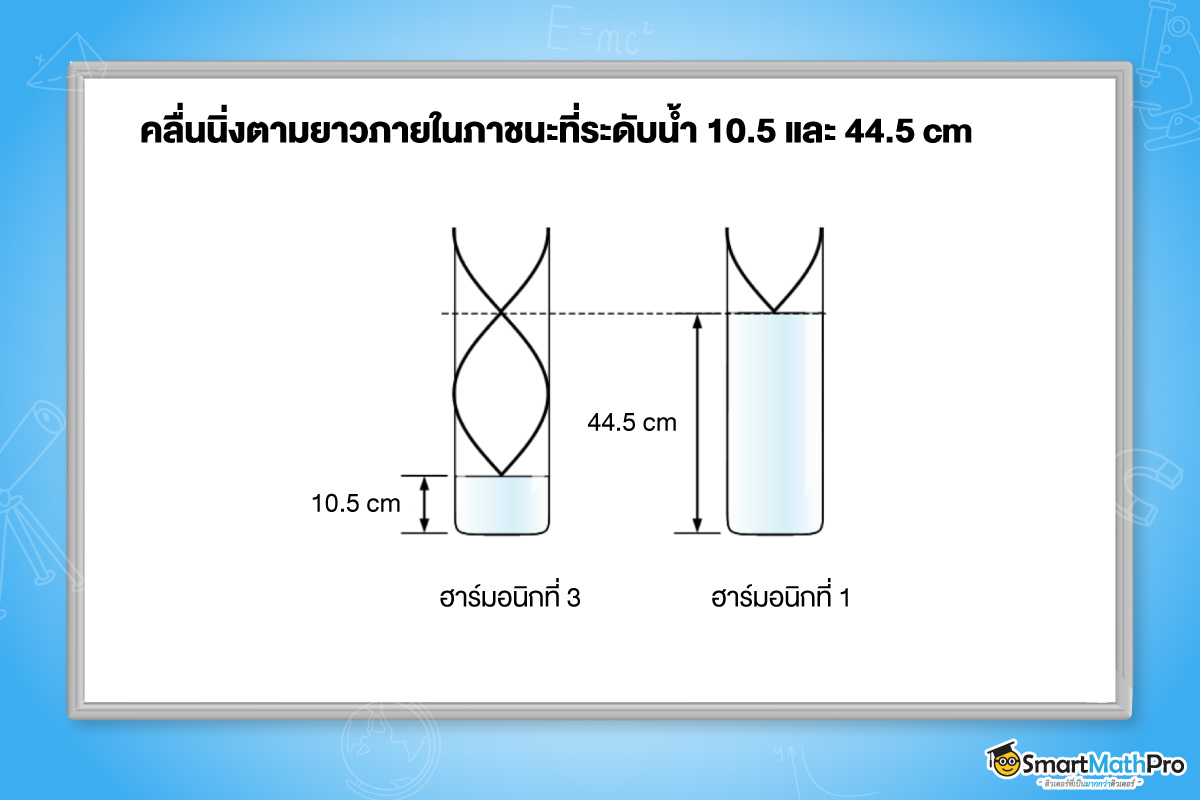
L=\frac{n\lambda }{4},n=1,3,5,…
L_{3}-L_{1}=\frac{\lambda }{2}
0.445-0.105=\frac{\lambda }{2}
\lambda =0.68m
ความถี่ของส้อมเสียง
f=\frac{v}{\lambda }
f=\frac{340}{0.68}
f=500Hz
ตอบ 5.6
ความเข้มเสียงที่ระยะใหม่ เมื่อระยะทางลดลงครึ่งหนึ่ง
\frac{I_{2}}{I_{1}}=\frac{\frac{P}{4\pi r_{2}^{2}}}{\frac{P}{4\pi r_{1}^{2}}}
\frac{I_{2}}{I_{1}}=\left ( \frac{r_{1}}{r_{2}} \right )^{2}
\frac{I_{2}}{I_{1}}=\left ( \frac{r_{1}}{\frac{r_{1}}{2}} \right )^{2}
\frac{I_{2}}{I_{1}}=4
การเปล่ียนแปลงระดับเสียง
\Delta \beta =10log\frac{I_{2}}{I_{1}}
\Delta \beta =10log4
\Delta \beta =10\times 0.6
\Delta \beta =6dB
ตอบ 3. ส้อมเสียง C และ 10 ครั้ง
ส้อมเสียงที่ทำให้ความถี่บีตเท่ากับ 5 เฮิรตซ์ ต้องเป็นส้อมเสียงที่มีความถี่ต่างจากแหล่งกำเนิดเสียง 5 เฮิรตซ์ ได้แก่
ส้อมเสียง B ความถี่ 430 เฮิรตซ์
f_{b}=\left | 435-430\right |=5Hz
ส้อมเสียง C ความถี่ 440 เฮิรตซ์
f_{b}=\left | 435-440\right |=5Hz
ดังนั้น ภายใน 2 วินาที เสียงบีตดังกล่าวจะมีเสียงดังเป็นจังหวะ 5 x 2 = 10 ครั้ง
จากตัวเลือก จึงต้องเลือกคำตอบเป็น ส้อมเสียง C และ 10 ครั้ง
ตอบ 1360.00 เมตร
เวลาเดินทางของเสียงในน้ำและอากาศต่างกัน 3 วินาที
t_{air}-t_{water}=3
\frac{d}{340}-\frac{d}{1360}=3
\frac{4d}{1360}-\frac{d}{1360}=3
\frac{3d}{1360}=3
d=1360
เป็นอย่างไรกันบ้างกับ “สรุปเนื้อหาเรื่อง เสียง ฟิสิกส์ ม.5” และแนวข้อสอบ A-Level ที่พี่นำมาฝากในวันนี้ หวังว่าจะช่วยให้น้อง ๆ ที่กำลังเตรียมตัวสอบทุกคนได้น้าา
แต่นอกจาก A-Level ฟิสิกส์แล้ว ในการยื่นเพื่อสมัคร น้อง ๆ อาจจะต้องใช้คะแนน A-Level อีกหลายวิชา และแต่ละวิชาก็ต้องอาศัยการเตรียมตัวค่อนข้างนาน สำหรับใครที่กลัวเตรียมตัวไม่ทันอยากจะประหยัดเวลาในการเตรียมสอบ
พี่ขอแนะนำคอร์สเรียนพิเศษสนาม A-Level ของ SmartMathPro ที่มีทั้ง A-Level คณิต 1, 2 / A-Level ภาษาอังกฤษ
/ A-Level ฟิสิกส์ / A-Level ภาษาไทย / A-Level สังคม เลยน้าา โดยสำหรับใครที่ไม่มีพื้นฐานก็สามารถเรียนได้
เพราะพี่สอนตั้งแต่ปูพื้นฐาน ไปจนถึงพาทำโจทย์ตั้งแต่ระดับง่ายไปจนถึงความยากใกล้เคียงกับข้อสอบจริงเลย แถมมีเทคนิคในการทำข้อสอบอีกเพียบที่จะช่วยให้น้อง ๆ ทำข้อสอบได้เร็วขึ้น > <
และสำหรับใครที่ยังไม่เริ่ม เริ่มติวตอนนี้ก็ยังทันน้าา แอบกระซิบว่าถ้าสมัครคอร์สตั้งแต่ตอนนี้พี่มี Unseen Mock Test ชุดพิเศษ 1 ชุด แถมฟรีไปให้ลองทำพร้อมสิทธิพิเศษประจำเดือนอีกมากมายด้วย ถ้าน้อง ๆ คนไหนสนใจคอร์สเตรียมสอบ A-Level สามารถ คลิก เข้ามาดูรายละเอียดได้เลยย
บทความ แนะนำ
A-Level ฟิสิกส์ 68 สอบอะไรบ้าง ? มีกี่ข้อ ? พร้อมตัวอย่างข้อสอบ
A-Level 68 คืออะไร? มีกี่ข้อ? มีวิชาอะไรบ้าง? สรุปพร้อมคลิปติว
A-Level คณิต 1 , A-Level คณิต 2 68 ออกสอบอะไรบ้าง? พร้อมคลิปติวฟรี
ข้อสอบ A-Level คณิต 1 และคณิต 2 68 มีบทไหนน่าเก็บและบทไหนเทได้บ้าง?
สรุป A-Level ไทย สังคม TCAS68 ออกสอบอะไรบ้าง? พร้อมคลิปติวฟรี
A-Level อังกฤษ 68 ออกสอบอะไรบ้าง? มีกี่ข้อ? พร้อมตัวอย่างข้อสอบ
A Level สอบวันไหน ? สรุปครบทุกกำหนดการ เช็กในบทความนี้เลย!
บทความ แนะนำ
A-Level ฟิสิกส์ 68 สอบอะไรบ้าง ? มีกี่ข้อ ? พร้อมตัวอย่างข้อสอบ
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
