น้อง ๆ รู้กันหรือเปล่าว่าเรื่อง ทฤษฎีบทพีทาโกรัส เป็นหนึ่งในเนื้อหาคณิตศาสตร์ที่สำคัญมาก เพราะสามารถนำไปปรับใช้กับเนื้อหาคณิต ม.ต้น ได้หลายบท รวมถึงต่อยอดในคณิต ม.ปลายได้อีกเยอะมาก
ดังนั้นถ้าน้อง ๆ คนไหนที่ยังไม่แม่นทฤษฎีบทพีทาโกรัส พี่แนะนำให้รีบมาทบทวนจากบทความนี้กันเลย เพราะพี่สรุปเนื้อหานี้มาให้อ่านกันแบบเข้าใจง่ายที่สุด และยังมีโจทย์ให้ฝึกทำด้วย ถ้าทุกคนพร้อมแล้ว ไปอ่านกันเลยยยย
น้อง ๆ น่าจะเคยได้เรียนและคุ้นหูคุ้นตากันเป็นอย่างดีกับเรื่อง “ทฤษฎีบทพีทาโกรัส” ที่พูดถึงความยาวด้านของรูป
สามเหล่ียมมุมฉากว่าเป็นทฤษฎีบทสำคัญที่เราจะใช้ต่อยอดในหลาย ๆ เรื่องเลย
ทฤษฎีบทนี้เรียนตอน ม.2 เทอม 1 และนำไปใช้แก้โจทย์ปัญหาหรือพิสูจน์ในบทที่เกี่ยวกับเรขาคณิต เช่น การหาพื้นที่ผิวและปริมาตรของรูปสามมิติ หรือโจทย์ประยุกต์ในบทสมการกำลังสองตัวแปรเดียว
นอกจากนี้ เนื้อหาทฤษฎีบทพีทาโกรัสยังมีส่วนเกี่ยวข้องกับเนื้อหา ม.ปลาย อีกหลายบทเลยไม่ว่าจะเป็น ฟังก์ชันตรีโกณมิติ, เรขาคณิตวิเคราะห์และภาคตัดกรวย, เวกเตอร์ และจำนวนเชิงซ้อน (รวมถึงมีการนำไปใช้ในวิชาวิทยาศาสตร์ด้วยน้าา)
ทฤษฎีบทพีทาโกรัส
ทฤษฎีบทพีทาโกรัส (Pythagoras’ theorem)
สำหรับรูปสามเหล่ียมมุมฉากใด ๆ กำลังสองของความยาวของด้านตรงข้ามมุมฉาก
เท่ากับผลบวกของกำลังสองของความยาวของด้านประกอบมุมฉาก
จากทฤษฎีบทข้างต้นสามารถสรุปได้ว่า
ตัวอย่างที่ 1 จากรูปสามเหล่ียมที่กำหนดให้ จงหาค่าของ x
วิธีทำ จากทฤษฎีบทพีทาโกรัส
จะได้ว่า x เป็นความยาวของด้านตรงข้ามมุมฉาก
แสดงว่า x^{2}=8^{2}+15^{2}\\= 64+225\\=289
ดังนั้น x=17
หมายเหตุ : สมการ x^{2}=289 มี 2 คำตอบคือ x=17 และ x=-17 เนื่องจาก x เป็นความยาวของด้านตรงข้ามมุมฉาก ค่า x ที่เป็นจำนวนลบจึงใช้ไม่ได้น้าา
ตัวอย่างที่ 2 จากรูปสามเหล่ียมที่กำหนดให้ จงหาค่าของ x
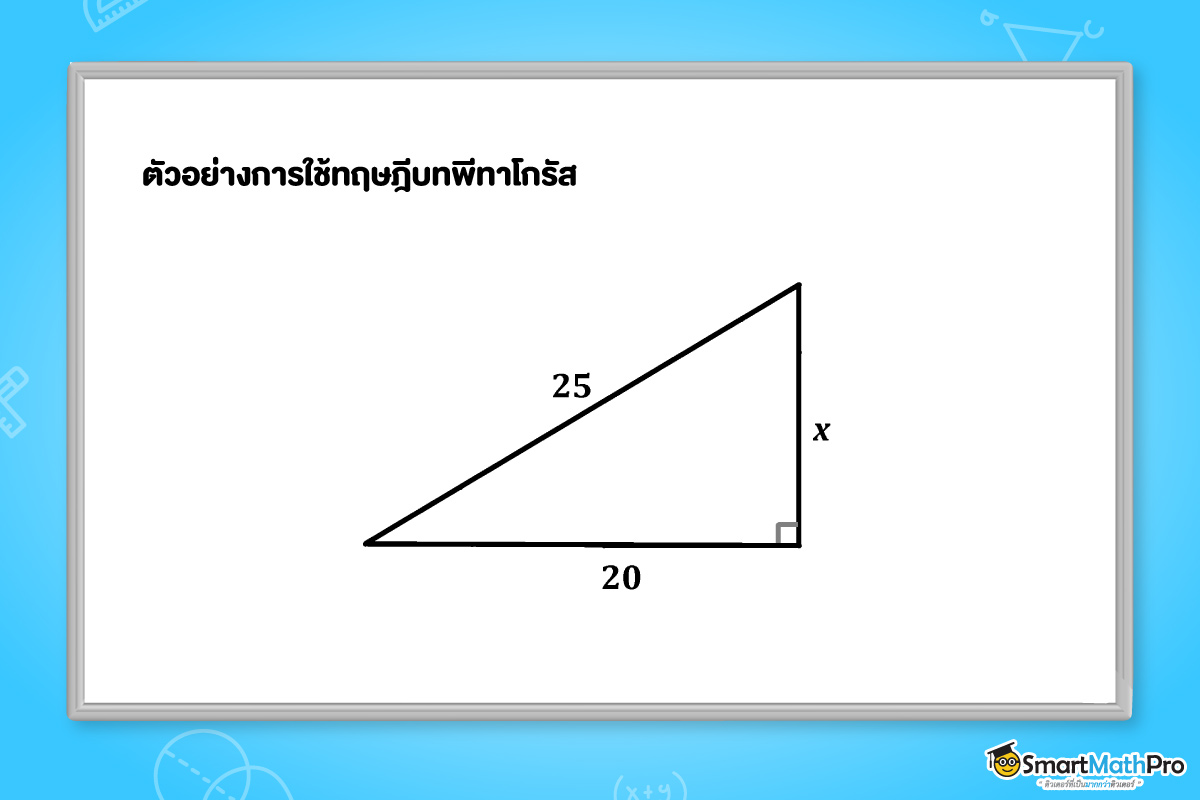
วิธีทำ จากทฤษฎีบทพีทาโกรัส
จะได้ว่า x เป็นความยาวของด้านประกอบมุมฉาก
แสดงว่า 25^{2}=x^{2}+20^{2}\\x^{2}=25^{2}-20^{2}\\=225
ดังนั้น x=15
เลขชุดพีทาโกรัสที่ควรรู้
เลขชุดพีทาโกรัส คือ ชุดตัวเลขที่ได้จากการคำนวณตามทฤษฎีบทแล้วเจอได้บ่อย ๆ เวลาต้องการใช้แก้โจทย์ปัญหา ซึ่งถ้าน้อง ๆ จำเลขชุดนี้ได้ จะทำให้เราแก้โจทย์ได้เร็วขึ้นด้วย โดยเลขชุดพีทาโกรัสที่นิยมใช้กันมีดังนี้
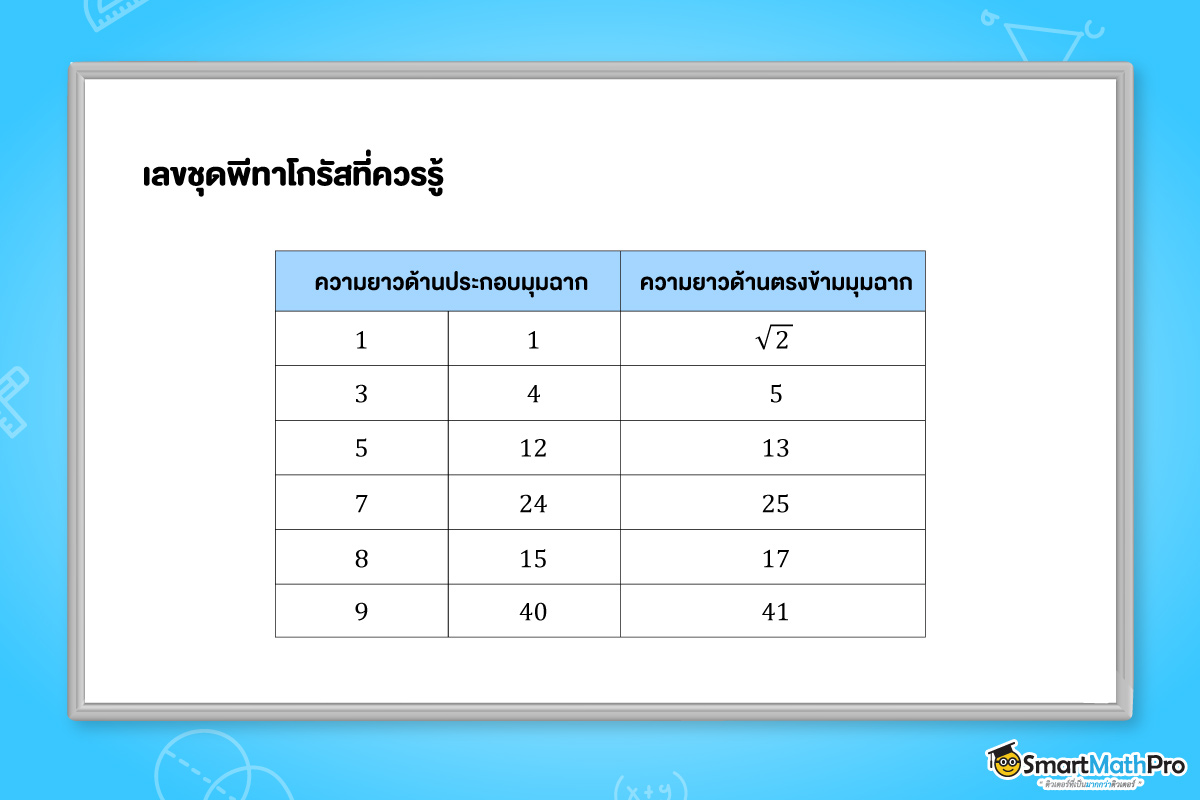
เลขชุดพีทาโกรัสจะใช้เมื่อรู้ความยาวด้าน 2 ด้านของรูปสามเหล่ียมมุมฉากจะสามารถหาความยาวอีกด้านหนึ่งได้ เช่น
- รูปสามเหล่ียมมุมฉากที่มีความยาวด้านคือ 3, 4, x โดยที่ x เป็นความยาวด้านตรงข้ามมุมฉาก
ดังนั้น เลขชุดพีทาโกรัสที่ใช้ได้ก็คือชุด 3, 4, 5
แสดงว่า x=5 - รูปสามเหล่ียมมุมฉากที่มีความยาวด้านคือ 6, 8, x โดยที่ x เป็นความยาวด้านตรงข้ามมุมฉาก
ดังนั้น เลขชุดพีทาโกรัสที่ใช้ได้ก็คือชุด 3, 4, 5
โดยปรับค่าเป็น 3\times 2, 4\times 2, 5\times 2
จะได้ 6, 8, 10
แสดงว่า x=10
หมายเหตุ : การปรับค่า จะต้องเป็นการนำเลขชุดพีทาโกรัสไปคูณหรือหารด้วยจำนวนเดียวกันเท่านั้น
ข้อระวัง : ต้องตรวจสอบว่าความยาวด้านที่นำมาพิจารณา เป็นความยาวด้านของด้านไหนด้วย เพราะเลขชุดพีทาโกรัสจะต้องอยู่ในด้านที่ถูกต้องถึงจะใช้ได้น้า
ตัวอย่างที่ 3 จากรูปสามเหล่ียมที่กำหนดให้ จงหาค่าของ x
วิธีทำ
จากโจทย์ จะได้ว่า รูปสามเหล่ียมนี้มีความยาวด้านคือ 10, x, 26 โดยที่ x เป็นความยาวของด้านประกอบมุมฉาก
ดังนั้น เลขชุดพีทาโกรัสที่ใช้คือ 5, 12, 13 โดยปรับค่าเป็น 5\times 2, 12\times 2, 13\times 2
จะได้ 10, 24, 26
ดังนั้น x=24
บทกลับของทฤษฎีบทพีทาโกรัส
จากเนื้อหาของบทความที่ผ่านมา น้อง ๆ จะรู้ว่าถ้ามีรูปสามเหล่ียมมุมฉากแล้วความยาวด้านจะมีความสัมพันธ์ตามทฤษฎีบทพีทาโกรัส ในทางกลับกันถ้านำความยาวด้านของรูปสามเหล่ียมที่สอดคล้องกับทฤษฎีบทพีทาโกรัสมาพิจารณาก็จะสามารถสรุปได้ว่ารูปที่พิจารณาอยู่เป็นรูปสามเหล่ียมมุมฉากได้เช่นกัน
บทกลับของทฤษฎีบทพีทาโกรัส (converse of Pythagoras’ theorem)
สำหรับรูปสามเหล่ียมมุมฉากใด ๆ ถ้ากำลังสองของความยาวของด้านด้านหนึ่ง
เท่ากับผลบวกของกำลังสองของความยาวของด้านอีกสองด้าน แล้วรูปสามเหล่ียมนั้นเป็นรูปสามเหล่ียมมุมฉาก
จากทฤษฎีบทข้างต้นสามารถสรุปได้ว่า
ตัวอย่างที่ 4 กำหนดให้รูปสามเหล่ียม ABC มีความยาวดังรูป
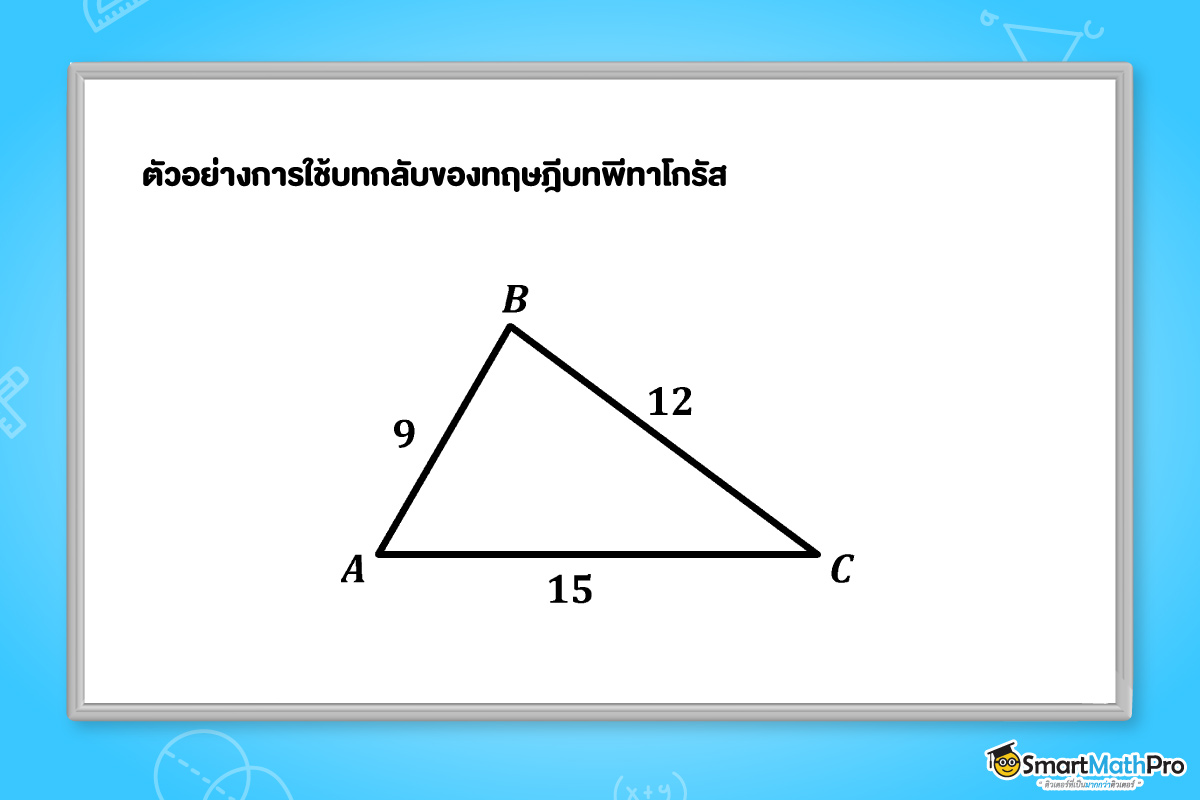
อยากทราบว่ารูปสามเหล่ียมABC เป็นรูปสามเหล่ียมมุมฉากหรือไม่
วิธีทำ จากรูป ให้ a=9, b=12 และ c=15
จะได้ a^{2}=81, b^{2}=144 และ c^{2}=225
ซึ่ง 225=81+144
แสดงว่า c^{2}=a^{2}+b^{2}
โดยบทกลับของทฤษฎีบทพีทาโกรัส สรุปได้ว่า รูปสามเหล่ียม ABC เป็นรูปสามเหล่ียมมุมฉาก
และนี่คือภาพรวมเนื้อหาทฤษฎีบทพีทาโกรัสที่พี่สรุปมาให้ทุกคนอ่านกันน้า จะเห็นว่าบทนี้สามารถนำไปใช้ได้ทั้งในเนื้อหาคณิต ม.ต้น และคณิต ม.ปลาย หลายบทเลย ดังนั้นถ้าน้อง ๆ มีพื้นฐานเรื่องนี้ดี ก็จะสามารถนำไปปรับใช้กับการเรียนคณิตศาสตร์บทที่เกี่ยวข้องได้ดีขึ้นนั่นเอง
ซึ่งถ้าน้อง ๆ อยากแม่นเรื่องนี้มากขึ้นพี่ก็แนะนำให้ฝึกทำโจทย์ / แบบฝึกหัดเพิ่มเติมกันเยอะ ๆ เลย แต่ถ้าใครยังกังวล กลัวว่าถ้าทบทวนหรือฝึกทำโจทย์เองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากได้คนช่วยไกด์
พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากก เรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมาก ใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
ตรีโกณมิติ ม.5 สรุปสูตรพร้อมแจกโจทย์แบบจัดเต็ม !!
เรขาคณิตวิเคราะห์ และภาคตัดกรวย ม.4 สรุปเนื้อหาพร้อมตัวอย่างโจทย์
เวกเตอร์ ม.5 สรุปทุกเนื้อหา พร้อมโจทย์ วิธีทำ และคลิปติวฟรี!
จำนวนเชิงซ้อน ม.5 คืออะไร ? สรุปเนื้อหา พร้อมตัวอย่างโจทย์
บทความ แนะนำ
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
