คณิตศาสตร์ ม.ต้น จะว่ายากก็ไม่ยาก จะว่าง่ายก็ไม่ง่าย (เอ๊ะ ยังไง!!) โดยเฉพาะในคณิตศาสตร์ ม.2 ซึ่งเป็นเนื้อหาที่อยู่ตรงกลางระหว่างด่านแรกที่เป็นการปรับพื้นฐานจากคณิตประถมสู่คณิต ม.ต้น อย่างคณิตศาสตร์ ม.1 และด่านสุดท้ายของคณิตศาสตร์ ม.ต้น ก่อนที่จะเลื่อนไปเรียนคณิต ม.ปลาย อย่างคณิตศาสตร์ ม.3 ทำให้เนื้อหาคณิตที่ได้เรียนในปีนี้จะมีทั้งง่ายและยากปน ๆ กันไป
สำหรับน้อง ๆ คนไหนที่อยู่ในช่วงกำลังจะขึ้น ม.2 หรืออยู่ ม.2 แล้วอยากรู้ว่าเนื้อหาคณิตศาสตร์ ม.2 ที่จะได้เรียนกันทั้ง เทอม 1 และ เทอม 2 เป็นยังไงบ้างเพื่อที่จะได้แพลนอ่านหนังสือหรือเตรียมตัวถูก พี่ก็เตรียมมาให้แล้วน้า ไปดูกันเลยดีกว่าว่าแต่ละเทอมจะเรียนเรื่องอะไรบ้าง และเนื้อหาประมาณไหน > <
คณิตศาสตร์ ม.2 ที่น้อง ๆ จะได้เรียนกัน มีทั้งหมด 11 บท มีทั้งหมด 2 เล่ม โดยน้อง ๆ จะได้เรียน 1 เล่ม ต่อ 1 เทอม ซึ่งพี่ก็แบ่งมาให้ดูแบบง่าย ๆ แล้วน้า ตามนี้เลยย
เนื้อหาคณิตศาสตร์ ม.2 เทอม 1 ประกอบด้วย
- ทฤษฎีบทพีทาโกรัส
- ความรู้เบื้องต้นเกี่ยวกับจำนวนจริง
- ปริซึมและทรงกระบอก
- การแปลงทางเรขาคณิต
- สมบัติของเลขยกกำลัง
- พหุนาม
เนื้อหาคณิตศาสตร์ ม.2 เทอม 2 ประกอบด้วย
- สถิติ (2)
- ความเท่ากันทุกประการ
- เส้นขนาน
- การให้เหตุผลทางเรขาคณิต
- การแยกตัวประกอบของพหุนามดีกรีสอง
คณิตศาสตร์ ม.2 เทอม 1 (เล่ม 1)
สำหรับคณิตศาสตร์ ม.2 เทอม 1 (เล่ม 1) จะมีจำนวนบทเรียนมากกว่าเทอม 2 หน่อยน้า แค่ 1 บทเท่านั้น !! น้อง ๆ ไม่ต้องกลัวเลยว่าเนื้อหาจะหนักเกินไป เพราะส่วนใหญ่บทเรียนในเทอมนี้จะเป็นการปูพื้นฐานเพื่อใช้ต่อยอด จะมีอะไรบ้างนั้น เลื่อนลงไปดูเล้ยยย
ทฤษฎีบทพีทาโกรัส
พีทาโกรัส เป็นชื่อของนักคณิตศาสตร์ชาวกรีก เป็นคนคิดทฤษฎีเกี่ยวกับความสัมพันธ์ระหว่างความยาวของด้านทั้งสามของสามเหลี่ยมมุมฉาก การเรียนทฤษฎีนี้จะช่วยต่อยอดให้น้อง ๆ เอาไปใช้ได้หลากหลายเลย เช่น ความยาวด้านของรูปสามเหลี่ยม หรือหาพื้นที่ และปริมาตรของรูปทรงเรขาคณิตบางรูปได้ด้วยน้า
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง ทฤษฎีบทพีทาโกรัส
- รูปสามเหลี่ยมมุมฉาก ในบทนี้มีเป็นการหาความยาวของด้านต่าง ๆ ของรูปสามเหลี่ยมมุมฉากจากสูตรที่กำหนดให้ น้อง ๆ จึงควรแยกได้ว่ารูปใดเป็นหรือไม่เป็นรูปสามเหลี่ยมมุมฉาก
- เลขยกกำลัง เนื่องจากสูตรที่กำหนดให้ มีการใช้เลขยกกำลังมาช่วยในการหาความยาวของด้าน จึงจะต้องรู้จักการเขียนและการหาเลขยกกำลังโดยเน้นที่เลขยกกำลังที่มีเลขชี้กำลังเป็น 2
รูปสี่เหลี่ยมจัตุรัสที่มีเส้นทแยงมุมยาว 15 เซนติเมตร จะมีพื้นที่กี่ตารางเซนติเมตร
ตอบ 112.5 ตารางเซนติเมตร
ความรู้เบื้องต้นเกี่ยวกับจำนวนจริง
ในคณิตศาสตร์ ม.1 น้อง ๆ ได้เรียนเรื่องจำนวนเต็ม ทศนิยมและเศษส่วนมาแล้ว เมื่อถึงคณิตศาสตร์ ม.2 ก็จะได้เกี่ยวกับจำนวนจริงและความสัมพันธ์ของจำนวนจริง เช่น จำนวนไหนเป็นจำนวนตรรกยะ, จำนวนอตรรกยะ หรือเขียนทศนิยมซ้ำในรูปเศษส่วน เป็นต้น
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง ความรู้เบื้องต้นเกี่ยวกับจำนวนจริง
- เลขยกกำลัง เป็นพื้นฐานการคำนวณที่ขาดไม่ได้เลย เพราะเราจะต่อยอดการคำนวณและพิจารณาจำนวนใหม่ ๆ ที่ท้าทายขึ้น
- การแปลงเศษส่วนให้เป็นทศนิยมซ้ำ เป็นความรู้พื้นฐานของระบบจำนวนจริงที่ควรรู้ เพื่อนำไปใช้ต่อยอดในการคำนวณยาก ๆ ได้
- ทฤษฎีบทพีทาโกรัส ใช้เป็นพื้นฐานในการสร้างจำนวนใหม่ ๆ โดยอาศัยความยาวของด้านจากรูปสามเหลี่ยมมาช่วย
ค่าของ \sqrt{64}\times \sqrt[3]{64} เท่ากับเท่าใด
ตอบ 32
ปริซึมและทรงกระบอก
บทนี้น้อง ๆ จะได้รู้จักกับรูปสามมิติอย่างปริซึมและทรงกระบอกมากขึ้นว่ามีลักษณะหรือองค์ประกอบยังไงบ้าง หาพื้นที่ผิวและปริมาตรยังไง เรื่องนี้อาจจะฟังดูยากไปหน่อย แต่น้อง ๆ ไม่ต้องห่วงน้า เพราะบทนี้ก็ต่อยอดมาจากเรื่องพื้นที่ของรูปเรขาคณิต, พื้นที่ 2 มิติและทฤษฎีบทพีทาโกรัสที่เรียนกันไปก่อนหน้านี้นั่นเองง
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง ปริซึมและทรงกระบอก
- พื้นที่ของรูปเรขาคณิตสองมิติ เช่น รูปสี่เหลี่ยมมุมฉาก รูปสามเหลี่ยม รูปสี่เหลี่ยมคางหมู เพื่อใช้ในการคำนวณหาพื้นที่ของหน้าตัดต่าง ๆ ของรูปทรงที่กำหนดให้
- ทฤษฎีบทพีทาโกรัส ใช้คำนวณหาความยาวของด้านที่ต้องการหาและใช้ในการแก้โจทย์ปัญหา
- ปริมาตรของทรงสี่เหลี่ยมมุมฉาก เป็นพื้นฐานการมองภาพสามมิติและต่อยอดการมองลักษณะของปริซึมและทรงกระบอก รวมไปถึงสูตรต่าง ๆ ในบทนี้
มีแก้วน้ำสองใบ แก้วใบที่หนึ่งวัดเส้นผ่านศูนย์กลางภายในได้ 6 เซนติเมตร วัดความสูงภายในแก้วได้ 16 เซนติเมตร ส่วนแก้วใบที่สองวัดเส้นผ่านศูนย์กลางภายในได้ 8 เซนติเมตร วัดความสูงภายในแก้วได้ 9 เซนติเมตร แก้วทั้งสองใบมีความหนา 2 มิลลิเมตรเท่ากัน และก้นแก้วทั้งสองหนา 1 เซนติเมตรเท่ากัน จากสถานการณ์ข้างต้น แก้วทั้งสองใบมีความจุต่างกันหรือไม่
ตอบ แก้วทั้งสองใบมีความจุเท่ากัน
การแปลงทางเรขาคณิต
การแปลงทางเรขาคณิต เป็นเรื่องที่น้อง ๆ จะได้เข้าใจความสัมพันธ์ของรูปเรขาคณิตมากขึ้น เพราะเรื่องนี้เรียนเกี่ยวกับการเคลื่อนไหวของเรขาคณิตผ่านการเลื่อนขนาน การสะท้อนและ การหมุนของรูปรูปหนึ่ง ถ้าน้อง ๆ เข้าใจและความสามารถอธิบายการแปลงทางเรขาคณิตนี้ได้ ก็จะช่วยต่อยอดในการเรียนได้อีกหลายเรื่องเลย เช่น ความเท่ากันทุกประการ หรือ กราฟของฟังก์ชันต่าง ๆ
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง การแปลงทางเรขาคณิต
- การสร้างพื้นฐานทางเรขาคณิต การสร้างรูปร่างทางเรขาคณิตเป็นความรู้พื้นฐานที่สำคัญสำหรับการสร้างรูปต้นแบบเพื่อใช้ในการแปลงทางเรขาคณิต
- สมบัติของเส้นขนาน นำความรู้เรื่องสมบัติของเส้นขนานมาช่วยเรื่องการแปลงทางเรขาคณิต
- ทฤษฎีบทพีทาโกรัส ใช้คำนวณหาความยาวของด้านของรูปต้นแบบหรือรูปที่ถูกแปลงทางเรขาคณิตแล้วและใช้ในการแก้โจทย์ปัญหาการแปลงทางเรขาคณิต
ข้อใดกล่าวไม่ถูกต้องเกี่ยวกับการแปลงทางเรขาคณิต
ก. ภาพที่ได้จากการสะท้อนจะเหมือนกับรูปต้นแบบและเท่ากันทุกประการเสมอ
ข. การสะท้อนรูปต้นแบบ 2 ครั้ง ผ่านเส้นตรงสองเส้นที่ตัดกัน ทำให้ภาพที่ได้มีลักษณะเหมือนกับการหมุน
ค. การสะท้อนรูปต้นแบบ 2 ครั้ง ผ่านเส้นตรงสองเส้นที่ขนานกัน ทำให้ภาพที่ได้มีลักษณะเหมือนกับการเลื่อนขนาน
ง. ระยะห่างระหว่างจุดบนรูปต้นแบบกับสันสะท้อน จะมากกว่าระยะห่างระหว่างเส้นสะท้อนกับจุดที่ได้จากการสะท้อนจุดนั้น
ตอบ ง. ระยะห่างระหว่างจุดบนรูปต้นแบบกับสันสะท้อน จะมากกว่าระยะห่างระหว่างเส้นสะท้อนกับจุดที่ได้จากการสะท้อนจุดนั้น
สมบัติของเลขยกกำลัง
ตอนเรียนคณิต ม.1 น้อง ๆ ได้เรียนเรื่องเลขยกกำลังไปแล้ว ในคณิตศาสตร์ ม.2 นี้ ทุกคนจะได้รู้จักกับสมบัติของเลขยกกำลัง, การดำเนินการของเลขยกกำลัง, เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มลบและเป็นเศษส่วน พี่ขอบอกว่าน้อง ๆ จะต้องเจอเลขยกกำลังอีกหลายบท ดังนั้นบทนี้จึงเป็นพื้นฐานสำคัญมาก ๆ สำหรับการเรียนคณิตศาสตร์เลยยย
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง สมบัติของเลขยกกำลัง
- จำนวนเต็ม เศษส่วน ทศนิยม เป็นพื้นฐานที่จำเป็นเพื่อใช้ในการดำเนินการต่าง ๆ ทางจำนวนภายในบทนี้
- เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก เป็นพื้นฐานที่สำคัญสำหรับต่อยอดจากเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวกเป็นจำนวนเต็ม
- สัญกรณ์วิทยาศาสตร์ เป็นการประยุกต์ใช้สมบัติของเลขยกกำลังเบื้องต้นที่ควรรู้
จงหาผลลัพธ์ของ \frac{3^0\times 49}{7^2}+\frac{3^5\times9}{27}
ตอบ 82
พหุนาม
เรื่องสุดท้ายของคณิตศาสตร์ ม.2 เทอม 1 (เล่ม 1) เป็นเรื่องพหุนามที่หลายคนอาจจะรู้จักหรือเคยได้ยินกันมาบ้าง ในบทนี้น้อง ๆ จะได้เรียนเกี่ยวกับการบวกและลบเอกนาม, การบวกและการลบพหุนาม, การคูณและการหารพหุนามด้วยเอกนาม เรื่องนี้จะช่วยให้น้อง ๆ เข้าใจเกี่ยวกับพหุนามมากขึ้น พร้อมต่อยอดในบทต่อ ๆ ไป !!
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง พหุนาม
- สมบัติของเลขยกกำลัง พหุนามจะต้องใช้พื้นฐานด้านการคำนวณเกี่ยวกับสมบัติของเลขยกกำลังในการคูณเอกนามด้วยเอกนาม
- สมบัติของการบวกและการคูณจำนวนจริง เป็นพื้นฐานการคำนวณที่จำเป็นอย่างยิ่งเพื่อต่อยอดการคำนวณที่สูงขึ้น ที่มีการใช้ตัวแปรในการดำเนินการต่าง ๆ รวมด้วย
จงเขียนพหุนาม -4x+5y+3-9+7x-6y ให้อยู่ในรูปผลสำเร็จ
ตอบ 3x-y-6
คณิตศาสตร์ ม.2 เทอม 2 (เล่ม 2)
หลังจากเห็นบทเรียนคณิตศาสตร์ ม.2 เทอม 1 กันไปแล้วเป็นยังไงบ้างง ? สำหรับเทอม 2 นี้จะมีจำนวนบทที่น้อยกว่าเทอม 1 น้า โดยน้อง ๆ จะได้เรียนทั้งหมด 5 บทด้วยกัน ใครอยากรู้แล้วว่าแต่ละบทเรียนอะไร พี่ก็สรุปมาให้ครบ !!
สถิติ (2)
ในคณิตศาสตร์ ม.1 น้อง ๆ ได้รู้จักกับแผนภูมิภาพ, แผนภูมิแท่ง, กราฟเส้น, แผนภูมิวงกลม แต่สำหรับเรื่องสถิติในคณิตศาสตร์ ม.2 นี้ ทุกคนจะได้เรียนเกี่ยวกับแผนภูมิอื่น ๆ เพิ่มขึ้น ได้แก่ แผนภาพจุด, แผนภาพต้น-ใบ, ฮิสโทแกรม นอกจากนี้เรายังจะได้หาและเปรียบเทียบค่ากลางของข้อมูลกันอีกด้วยย
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง สถิติ (2)
- ความหมายของสถิติและกระบวนการทางสถิติ เพื่อทำให้รู้ขั้นตอนเบื้องต้นของการจัดการข้อมูลทางสถิติ
- ข้อมูลเชิงคุณภาพและข้อมูลเชิงปริมาณ สามารถแบ่งแยกข้อมูลที่จะนำมาใช้ในบทนี้ได้ว่าเป็นข้อมูลลักษณะใด และสามารถต่อยอดได้ว่าค่ากลางตัวใดเหมาะสมกับข้อมูลแบบใด
- ความรู้เบื้องต้นเกี่ยวกับจำนวนจริง ใช้เป็นการคำนวณพื้นฐานเบื้องต้น
โรงเรียนแห่งหนึ่งจำแนกคนงานออกเป็น 2 กลุ่ม คือ กลุ่มคนสวนและกลุ่มแม่บ้าน โดยที่กลุ่มคนสวนและกลุ่มแม่บ้านจะได้รับค่าจ้างรายวันวันละ 380 และ 350 บาท ตามลำดับ ถ้าโรงเรียนจ้างคนสวน 5 คน และแม่บ้าน 10 คน อยากทราบว่าคนงานของโรงเรียนแห่งนี้มีรายได้เฉลี่ยวันละกี่บาท
ตอบ 360 บาท
ความเท่ากันทุกประการ
สำหรับเนื้อหาความเท่ากันทุกประการ น้อง ๆ จะได้เรียนเกี่ยวกับความเท่ากันทุกประการของรูปเรขาคณิต, รูปสามเหลี่ยม และรูปสามเหลี่ยม 2 รูปที่มีความสัมพันธ์กันแบบ ด้าน-มุม-ด้าน / มุม-ด้าน-มุม / ด้าน-ด้าน-ด้าน / มุม-มุม-ด้าน / ฉาก-ด้าน-ด้าน แถมยังมีการเขียนพิสูจน์ข้อความด้วย เรียกได้ว่าเป็นบทแรกของวิชาคณิตศาสตร์ ม.ต้น เลยที่มีการพิสูจน์ แตกต่างกับบทที่ผ่าน ๆ มาที่เน้นการทำความเข้าใจและการคำนวณเป็นหลัก
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง ความเท่ากันทุกประการ
- การสร้างทางเรขาคณิตการสร้างรูปร่างทางเรขาคณิตเป็นความรู้พื้นฐานสำหรับการสร้างรูปต่าง ๆ
- รูปเรขาคณิตสองมิติและสามมิติเป็นความรู้เบื้องต้นสำหรับการมองภาพรูปร่างและรูปทรงต่าง ๆ
- ทฤษฎีบทพีทาโกรัส ใช้คำนวณหาความยาวของด้านและใช้ในการแก้โจทย์ปัญหา
- มุมที่เกิดจากเส้นตัดตัดเส้นขนาน เพื่อนำมาประยุกต์ใช้และช่วยในการหาขนาดของมุมต่าง ๆ โดยอาศัยความรู้เกี่ยวกับเส้นขนานและเส้นตัดที่ตัดกับเส้นขนาน
- การแปลงทางเรขาคณิต เพื่อนำมาประยุกต์ใช้และช่วยในการแก้โจทย์ปัญหา
รูปสามเหลี่ยมที่กำหนดให้ต่อไปนี้ เท่ากันทุกประการหรือไม่ ถ้าเท่ากันทุกประการให้บอกว่าเท่ากันทุกประการด้วยความสัมพันธ์แบบใด
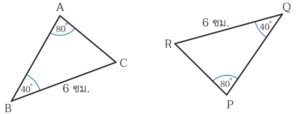
ตอบ เท่ากันทุกประการ เพราะมีความสัมพันธ์แบบ มุม-ด้าน-มุม หรือ มุม-มุม-ด้าน
เส้นขนาน
สำหรับบทเรียนเรื่องเส้นขนาน น้อง ๆ จะได้เรียนเรื่อง เส้นขนานและมุมภายใน, เส้นขนานและมุมแย้ง, เส้นขนานมุมภายนอกกับมุมภายใน, เส้นขนานและรูปสามเหลี่ยม และเขียนพิสูจน์ทฤษฎีบทเกี่ยวกับรูปสามเหลี่ยมโดยจะใช้สมบัติของเส้นขนานมาอธิบายด้วย
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง เส้นขนาน
- มุมตรงข้าม มุมตรง มุมภายใน มุมภายนอก มุมแย้งเป็นความรู้ที่จำเป็นอย่างมากสำหรับบทนี้เพื่อใช้ในการหาขนาดของมุมจากสมบัติต่าง ๆ
- ความเท่ากันทุกประการของรูปสามเหลี่ยม เพื่อนำไปช่วยในการแก้โจทย์ปัญหาที่มีรูปสามเหลี่ยมปรากฎ
- ผลบวกของขนาดของมุมภายในของรูปสามเหลี่ยม เพื่อนำไปช่วยหาขนาดของมุมจากโจทย์ปัญหาที่กำหนดให้
กำหนดให้ \bar{AB} // \bar{CD} และ \bar{CD} // \bar{EF} โดยมีระยะห่างระหว่าง \bar{AB} และ \bar{EF} เท่ากับ 20 เซนติเมตร และมีระยะห่างระหว่าง \bar{CD} และ \bar{EF} เท่ากับ 15 เซนติเมตร จงหาระยะห่างระหว่าง \bar{AB} และ \bar{CD}
ตอบ 5 เซนติเมตร, 35 เชนติเมตร ตามลำดับ
การให้เหตุผลทางเรขาคณิต
มีใครลืมเนื้อหาคณิตศาสตร์ ม.1 ไปแล้วบ้างงง รีบหยิบหนังสือมาทบทวนเลยกันดีกว่าน้าา > < เพราะบทการให้เหตุผลทางเรขาคณิตนี้จะเป็นการนำความรู้เรื่องการสร้างทางเรขาคณิตในเนื้อหาคณิตศาสตร์ ม.1 กับการพิสูจน์มาใช้ร่วมกัน
โดยน้อง ๆ จะได้เรียนเกี่ยวกับพื้นฐานการให้เหตุผลทางเรขาคณิต, การสร้างและให้เหตุผลเกี่ยวกับการสร้าง, การให้เหตุผลเกี่ยวกับรูปสามเหลี่ยมและรูปสี่เหลี่ยม บทนี้พี่บอกเลยว่าถ้าพื้นฐานแน่น ก็ไม่มีอะไรที่ต้องกลัว !!
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง การให้เหตุผลทางเรขาคณิต
- ความรู้พื้นฐานและสมบัติของรูปเรขาคณิตสองมิติ
- การสร้างพื้นฐานทางเรขาคณิต
- ทฤษฎีบทพีทาโกรัส
- การแปลงทางเรขาคณิต
- ความเท่ากันทุกประการของรูปสามเหลี่ยม
- เส้นขนาน
เนื่องจากบทนี้เป็นทักษะทางคณิตด้านการให้เหตุผลทางเรขาคณิต ทำให้ความรู้พื้นฐานที่เกี่ยวกับเรขาคณิตทั้งหมดจึงมีความสำคัญอย่างมาก เพราะความรู้ต่าง ๆ ที่กล่าวมาจะถูกนำมาเป็นเหตุผลประกอบการพิสูจน์ข้อความคาดการณ์หรือสมบัติต่าง ๆ ด้วย
จงพิจารณาว่ารูปสามเหลี่ยมที่กำหนดให้ต่อไปนี้เป็นรูปสามเหลี่ยมชนิดใด (รูปสามเหลี่ยมหน้าจั่ว รูปสามเหลี่ยมมุมฉาก หรือ รูปสามเหลี่ยมด้านเท่า) เพราะเหตุใด (ตอบได้มากกว่า 1 คำตอบ)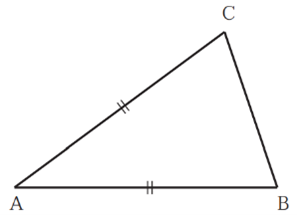
แนวคิดในการให้เหตุผล
\Delta ABC เป็นรูปสามเหลี่ยมหน้าจั่ว เพราะ มีด้านยาวเท่ากันสองด้าน
การแยกตัวประกอบของพหุนามดีกรีสอง
น้อง ๆ หลายคนอาจเคยคิดว่าการแยกตัวประกอบมีแค่ในจำนวนนับ พอเห็นชื่อบทนี้ก็เลยทำให้งงไปตาม ๆ กัน ที่จริงแล้วพหุนามก็สามารถแยกตัวประกอบได้เหมือนกันน้า ในบทนี้น้อง ๆ จะได้เรียนรู้เกี่ยวกับ การแยกตัวประกอบพหุนามโดยใช้สมบัติการแจกแจง, การแยกตัวประกอบของพหุนามดีกรีสองตัวแปรเดียว, การแยกตัวประกอบของพหุนามดีกรีสองที่เป็นกำลังสองสมบูรณ์ และการแยกตัวประกอบของพหุนามดีกรีสองที่เป็นผลต่างกำลังสอง ซึ่งบทนี้ถือว่าเป็นอีกบทที่สำคัญไม่แพ้เรื่องอื่นเลยน้า เพราะจะถูกเอาไปต่อยอดกับเนื้อหาคณิตศาสตร์ ม.ปลายนั่นเองง
เนื้อหาที่ควรรู้ก่อนเรียน คณิต ม.2 เรื่อง การแยกตัวประกอบของพหุนามดีกรีสอง
- ความรู้เกี่ยวกับเรื่องการแยกตัวประกอบของจำนวนนับ เป็นพื้นฐานที่สำคัญเพื่อให้เห็นภาพการแยกตัวประกอบที่เป็นจำนวนแล้วต่อยอดมาเป็นตัวแปร
- การบวก การลบ การคูณพหุนาม และการหารพหุนามด้วยเอกนาม เป็นความรู้พื้นฐานที่จำเป็นอย่างมากเนื่องจากบทนี้จะเกี่ยวกับการจัดการเอกนามและพหุนามเป็นหลัก
พหุนาม x^2-1+z(x-1) เท่ากับพหุนามในข้อใด
ก. (x-1)(x+z-1)
ข. (x-1)(x+z+1)
ค. (x+1)(x+z+1)
ง. (x+1)(x+z-1)
ตอบ ข. (x-1)(x+z+1)
หลังจากได้เห็นเนื้อหาที่จะได้เรียนในคณิตศาสตร์ ม.2 ทั้งเทอม 1 และเทอม 2 ไปแล้ว น้อง ๆ ก็คงจะเห็นว่ามีหลายเรื่องที่ต่อยอดมาจากคณิตศาสตร์ ม.1 และยังต่อยอดไปใช้เรียนคณิตศาสตร์ม.3 ได้อีกด้วย ถ้าใครอยากกลับไปทบทวนเนื้อหาตอนม.1 หรืออยากดูเนื้อหาของคณิตม.3 เพื่อเตรียมไว้ล่วงหน้า ก็สามารถคลิกไปดูบทความเนื้อคณิต ม.ต้นได้น้า ว่าแต่ละชั้นเรียนอะไรบ้าง พี่สรุปมาให้แล้วว >> คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
ใครที่รู้สึกว่าเนื้อหาคณิตศาสตร์มันยากขึ้นเรื่อย ๆ พี่จะบอกว่าไม่แปลกใจเลยน้าที่เราจะรู้สึกแบบนั้น ซึ่งความยากของบทเรียนจะเพิ่มขึ้นตามระดับชั้นอยู่แล้ว ไม่ใช่แค่วิชาคณิตศาสตร์ แต่การเรียนคณิตจะไม่ใช่ว่ามาถึงก็เรียนบทยาก ๆ เลย ยังไงก็ตามน้อง ๆ จะได้เริ่มเรียนจากพื้นฐานก่อนแล้วไต่ระดับขึ้นไปบทที่ยากขึ้น
ดังนั้นถ้าใครเรียนแล้วไม่เข้าใจ ปัญหาส่วนหนึ่งอาจมาจากพื้นฐานไม่แน่นพอก็ได้ พี่แนะนำให้น้อง ๆ ดูเนื้อหาที่ต้องรู้ก่อนเรียนแล้วกลับไปทบทวนบทเรียนที่ผ่านมา หรือฝึกทำโจทย์เพิ่มก็อาจจะช่วยให้เข้าใจมากขึ้นน้า สู้ ๆ ทุกคน พี่เชื่อว่าทุกคนทำได้แน่นอนนน
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
คณิตศาสตร์ ม.3 เทอม 1, เทอม 2 เรียนอะไรบ้าง ? อัปเดตตาม สสวท.
สรุป อสมการเชิงเส้นตัวแปรเดียว ม.3 พร้อมแจกโจทย์และเฉลย
สรุป แยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง ม.3 พร้อมโจทย์+เฉลย
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
สรุปคณิตศาสตร์ “ความคล้าย ม.3” พร้อมแจกโจทย์ปัญหาและเฉลยฟรี !!
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
Twitter : @PanSmartMathPro
Tiktok : @pan_smartmathpro
