เรขาคณิตวิเคราะห์ และภาคตัดกรวย ม.4 สรุปเนื้อหาพร้อมตัวอย่างโจทย์

ดูจากชื่อเรื่องแล้ว มีใครคุ้น ๆ บ้างงง ว่าเราเคยเรียนเรื่องที่เกี่ยวกับเรขาคณิตมาแล้วตอน ม.ต้น และในม.ปลายนี้ น้อง ๆ จะกลับมาเรียนเรื่องเรขาคณิตอีกครั้ง แบบลึกขึ้นในชื่อบท “เรขาคณิตวิเคราะห์ และภาคตัดกรวย ม.4” แน่นอนว่าพอเป็นคณิตม.ปลาย เนื้อหาอาจจะยากขึ้นมาหน่อย แต่ไม่ต้องกลัวว เพราะพี่เตรียมสรุปเนื้อหามาให้แล้ว ใครอยากเข้าใจเรื่องเรขาคณิตวิเคราะห์และภาคตัดกรวย ม.4 ให้มากขึ้น รีบเลื่อนลงไปดูข้างล่างนี้กันได้เลยน้าา

สนใจหัวข้อไหน ... กดอ่านเลย

เรขาคณิตวิเคราะห์ ม.4

อย่างที่พี่ได้เล่าไปตอนต้นแล้วว่า น้อง ๆ เคยเรียนการสร้างส่วนของเส้นตรงกันมาแล้ว ซึ่งจะใช้ความรู้ทางเรขาคณิตเป็นส่วนใหญ่ แต่ในหัวข้อนี้น้อง ๆ จะได้นำความรู้เรื่องเรขาคณิตมาต่อยอด โดยจะเชื่อมโยงความรู้ระหว่างพีชคณิตและเรขาคณิตเข้าด้วยกันเพื่อช่วยแก้ไขปัญหาต่าง ๆ

ระยะห่างระหว่างจุดสองจุด

เช่น จุด $P(3,8)$ กับจุด $Q(6,4)$ จะได้ว่า

$d=\sqrt{(3-6)^{2}+(8-4)^{2}}=\sqrt{9+16}=\sqrt{25}=5$

จุดกึ่งกลางของส่วนของเส้นตรง

เช่น จุด $P(-1,6)$ กับจุด $Q(5,4)$ จะได้ว่าจุดกึ่งกลางระหว่าง $(-1,6)$ และ $(5,4)$ คือ $\left ( \frac{-1+5}{2},\frac{6+4}{2} \right )=\left ( 2,5 \right )$

ระยะห่างระหว่างเส้นตรงกับจุด

เช่น $(4, 1)$ กับเส้นตรง $5x-12y+18=0$ จะได้ว่า

$d=\frac{\left |4\cdot 5+1(-12)+18 \right |}{\sqrt{5^{2}+(-12)^{2}}}=\frac{\left | 20-12+18 \right |}{\sqrt{169}}=\frac{26}{13}=2$

ระยะห่างระหว่างเส้นตรง

เช่น เส้นตรง $6x-8y+4=0$ กับ $6x-8y-16=0$ จะได้ว่า
$d=\frac{\left |4-(-16) \right |}{\sqrt{6^{2}+(-8)^{2}}}=\frac{\left | 4+16 \right |}{\sqrt{100}}=\frac{20}{10}=2$

เส้นตรง

เส้นตรง เราสามารถเขียนให้อยู่ในรูปสมการเส้นตรง คือ $y=mx+c$ หรือรูปทั่วไปของสมการเส้นตรง คือ $Ax+By+C=0$ เมื่อ $A, B, C$ เป็นค่าคงตัว โดยที่ $A$ และ $B$ ไม่เป็นศูนย์พร้อมกัน

ความชันของเส้นตรง (m)

เราสามารถรู้ความชันของเส้นตรง ได้จากสมการ $y=mx+c$ หรือจากสูตรต่อไปนี้

ความชันของเส้นตรงที่ผ่านจุด $(x_{1},y_{1})$ และ $(x_{2},y_{2})$ เมื่อ $x_{1}\neq x_{2}$ คือ $m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$

เส้นตรงขนานและตั้งฉาก

ให้ $m_{1}$ และ $m_{2}$ เป็นความชันของเส้นตรง $l_{1}$ และ $l_{2}$ ตามลำดับ จะได้ว่า
เส้นตรง $l_{1}$ และ $l_{2}$ ขนานกัน เมื่อ $m_{1}=m_{2}$
เส้นตรง $l_{1}$ และ $l_{2}$ ตั้งฉากกัน เมื่อ $m_{1}m_{2}=-1$

เช่น สมมติเส้นตรง 2 เส้นที่ต่างกัน เส้นตรงที่มีความชันเป็น 2 จะขนานกับเส้นตรงที่มีความชันเป็น 2 เนื่องจากค่าของความชันเท่ากัน จะได้ว่าเส้นตรงขนานกัน และเส้นตรงที่มีความชันเป็น 2 จะตั้งฉากกับเส้นตรงที่มีความชันเป็น $-\frac{1}{2}$ เพราะ $2\times \left ( -\frac{1}{2} \right ) =-1$

ภาคตัดกรวย ม.4

ในหัวข้อนี้ เราจะศึกษาภาคตัดกรวยโดยใช้วิธีทางเรขาคณิตวิเคราะห์มาช่วย โดยนำระนาบมาตัดกรวยกลมตรงในลักษณะที่ต่างกัน ซึ่งจะตัดโดยอิงจากแกนที่อยู่ในแนวตั้งตามรูปด้านล่างและสมการเส้นตรงหรือตัวก่อกำเนิด ดังนั้น ภาคตัดกรวยที่น้อง ๆ กำลังจะเรียนนั่นก็คือรูปในระนาบที่เกิดจากการตัดกันของระนาบกับกรวยนั่นเอง

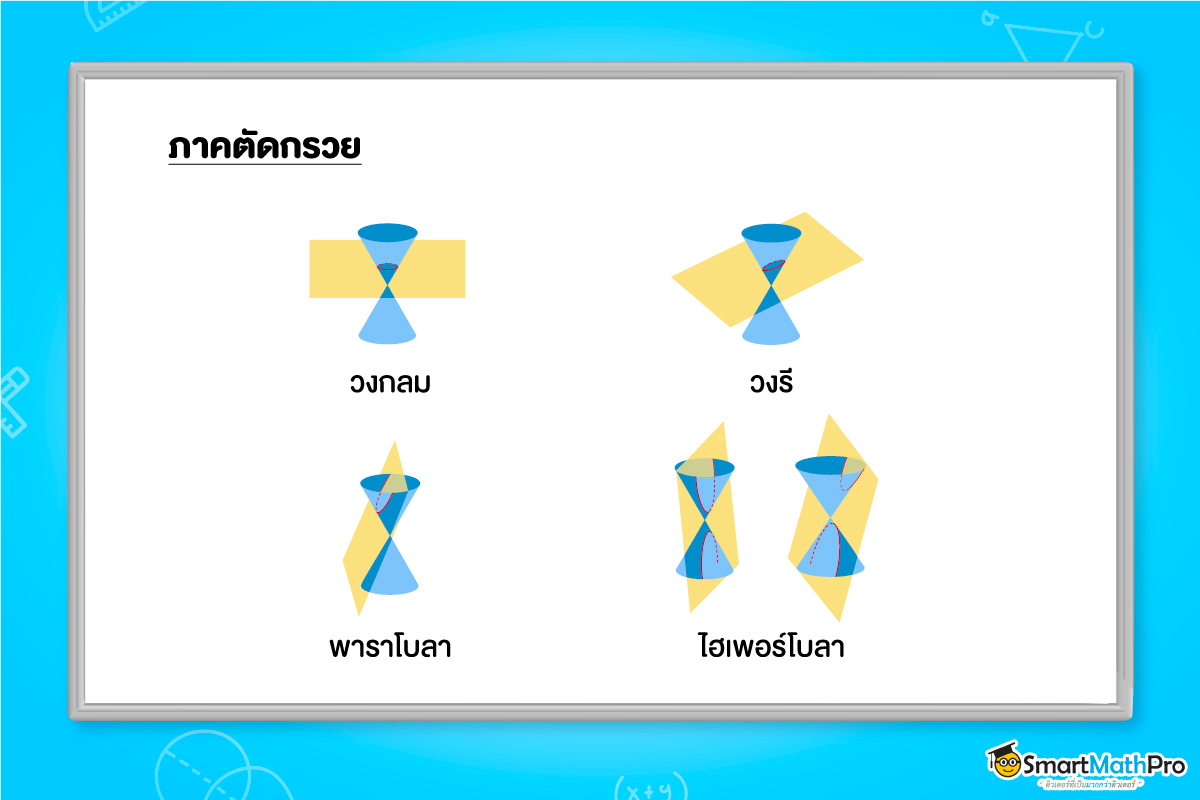
ถ้าเราตัดโดยใช้ระนาบ (แผ่นสีเหลือง) ตามรูป จะได้ว่า

ระนาบตั้งฉากกับแกนของกรวยข้างเดียว จะได้ภาคตัดกรวยที่เรียกว่า วงกลม
ระนาบไม่ตั้งฉากกับแกนของกรวย แต่ทำมุมกับแกนของกรวยขนาดใหญ่ค่าหนึ่ง ระนาบจะตัดกรวยข้างเดียว ได้ภาคตัดกรวยที่เรียกว่า วงรี
ระนาบขนานตัวก่อกำเนิดของกรวย ระนาบจะตัดกรวยข้างเดียว ได้ภาคตัดกรวยที่เรียกว่า พาราโบลา
ระนาบขนานกับแกนของกรวย ระนาบจะตัดกรวยสองข้าง จะได้ภาคตัดกรวยที่เรียกว่า ไฮเพอร์โบลา

วงกลม

วงกลม คือ เซตของจุดทั้งหมดในระนาบที่ห่างจากจุด ๆ หนึ่งที่ตรึงอยู่กับที่เป็นระยะทางคงตัว จุดที่ตรึงอยู่กับที่นี้เรียกว่า จุดศูนย์กลาง (center) ของวงกลม และส่วนของเส้นตรงที่มีจุดศูนย์กลางและจุดบนวงกลมเป็นจุดปลายเรียกว่า รัศมี (radius) ของวงกลม

ตัวอย่างที่ 1 จงจัดรูปสมการ $x^2+y^2+x+2y+1=0$ ให้อยู่ในรูปแบบมาตรฐาน

วิธีทำ
$x^2+y^2+x+2y+1=0$
$(x^2+x)+(y^2+2y)+1=0$
$\left (x^2+x+\left (\frac{1}{2} \right )^2 \right )+(y^2+2y+1^2)+1-\left (\frac{1}{2} \right )^2-1^2=0$
$\left ( x+\frac{1}{2} \right )^2+(y+1)^2=\frac{1}{4}$

วงรี

วงรี คือ เซตของจุดทั้งหมดในระนาบซึ่งผลบวกของระยะทางจากจุดใด ๆ ในเซตนั้นไปยังจุดที่ตรึงอยู่กับที่สองจุดมีค่าคงตัว โดยค่าคงตัวนี้ต้องมากกว่าระยะห่างระหว่างจุดที่ตรึงอยู่กับที่ทั้งสองจุด เรียกจุดที่ตรึงอยู่กับที่ทั้งสองจุดนี้ว่า โฟกัส (focus) ของวงรี

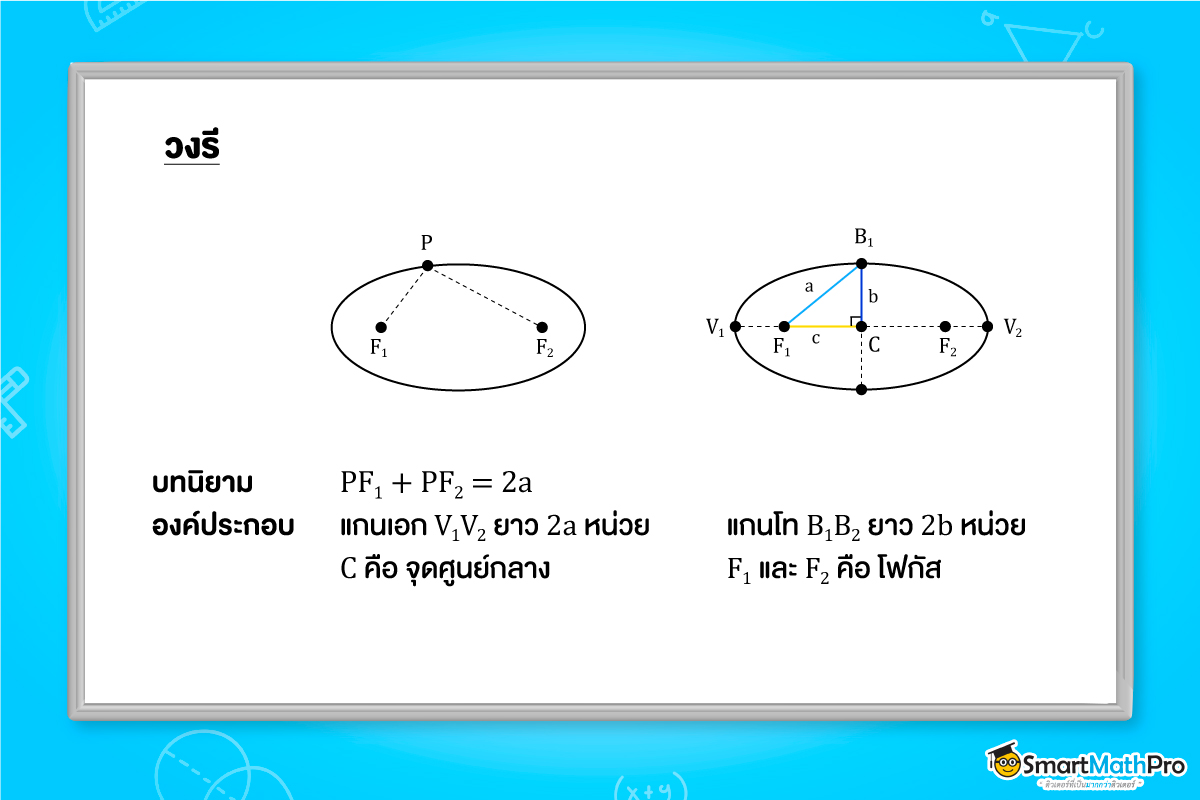
โดยวงรีที่เราจะศึกษาจะมีสองรูปน้า นั่นก็คือวงรีที่มีแกนเอกอยู่ในแนวนอน (วงรีแนวนอน) และวงรีที่มีแกนเอกในแนวตั้ง (วงรีแนวตั้ง) ซึ่งรูปแบบมาตรฐานของสมการของวงรีก็จะมี 2 แบบเช่นกัน

ตัวอย่างที่ 2 จงจัดรูปสมการ $x^2+4y^2-6x+16y+21=0$ ให้อยู่ในรูปแบบมาตรฐาน

วิธีทำ
$x^2+4y^2-6x+16y+21=0$

$(x^2-6x)+4(y^2+4y)=-21$

$(x^2-6x+9)+4(y^2+4y+4)=-21+9+16$

$(x-3)^2+4(y+2)^2=4$

$\frac{(x-3)^2}{4}+\frac{(y+2)^2}{1}=1$

$\frac{(x-3)^2}{4}+(y+2)^2=1$

พาราโบลา

น้อง ๆ อาจเคยรู้จักพาราโบลามาแล้วบ้างจากการเรียนเรื่องกราฟของฟังก์ชันกำลังสองหรือพาราโบลา ในระดับชั้น ม.3 ส่วนบทภาคตัดกรวยนี้ พี่จะพาน้องมารู้จักพาราโบลาเพิ่มเติม จะเป็นยังไงไปอ่านต่อกันเลย

พาราโบลา คือ เซตของจุดทั้งหมดในระนาบซึ่งห่างจากจุดที่ตรึงอยู่กับที่จุดหนึ่งและเส้นตรงที่ตรึงอยู่กับที่เส้นหนึ่งเป็นระยะเท่ากัน จุดที่ตรึงอยู่กับที่นี้ เรียกว่า โฟกัสของพาราโบลา และเส้นที่ตรึงอยู่กับที่นี้เรียกว่า เส้นบังคับ หรือ ไดเรกตริกซ์ ของพาราโบลา

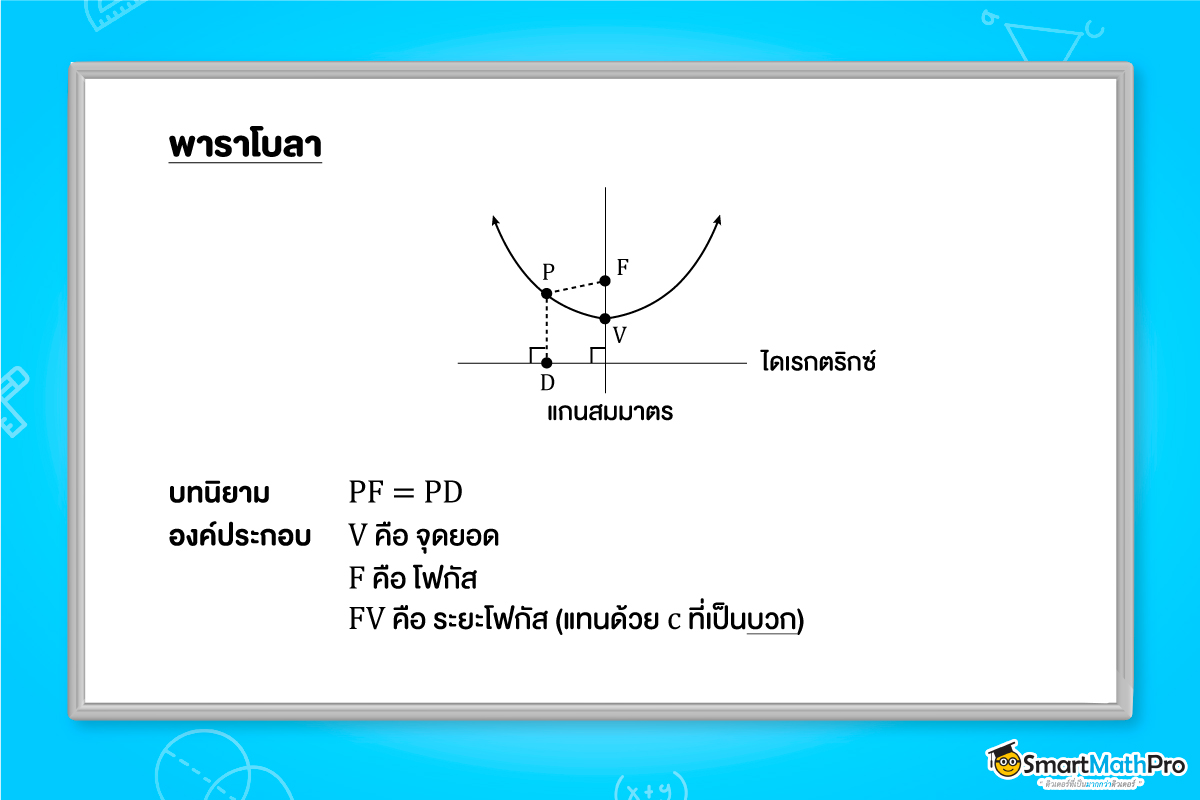
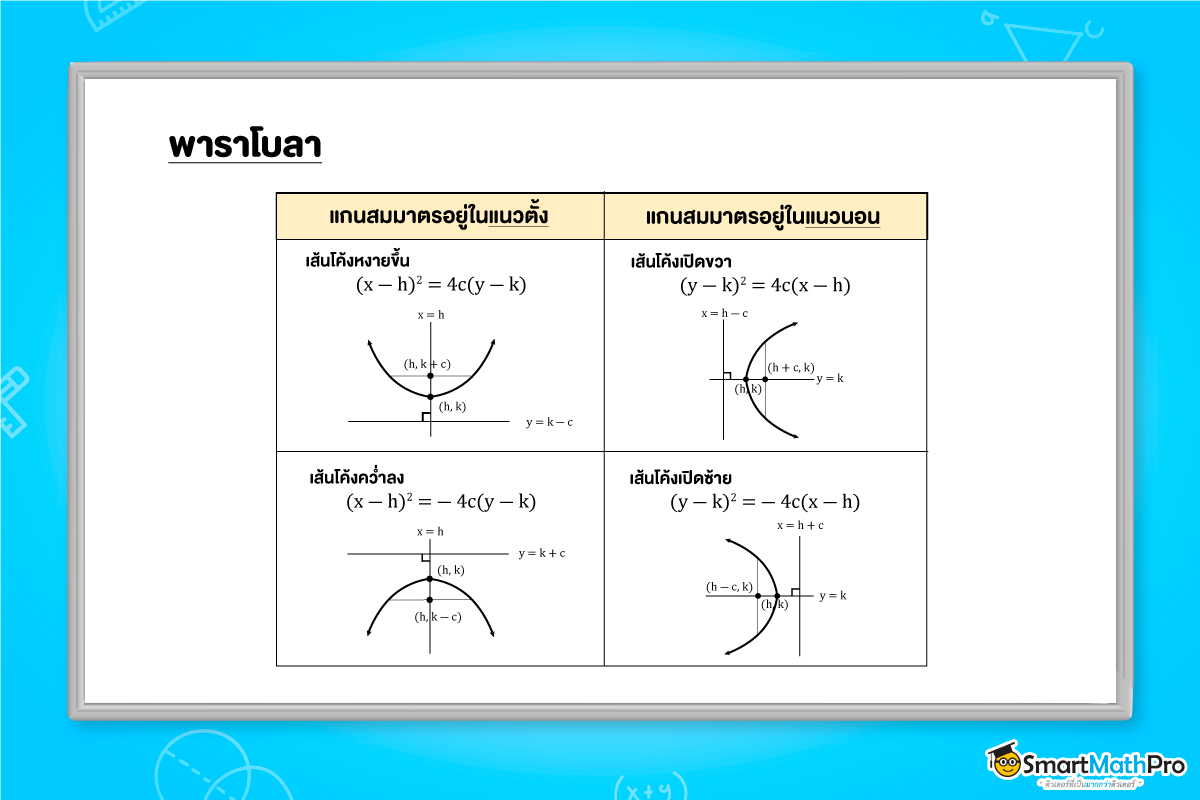
พาราโบลาสามารถวาดได้ 4 แบบตามรูปแบบมาตรฐานของสมการพาราโบลา ซึ่งก็คือ

พาราโบลาหงายขึ้น
จะมีสมการรูปแบบมาตรฐานคือ $(x-h)^{2}=4c(y-k)$
พาราโบลาคว่ำลง
จะมีสมการรูปแบบมาตรฐานคือ $(x-h)^{2}=-4c(y-k)$
พาราโบลาเปิดขวา
จะมีสมการรูปแบบมาตรฐานคือ $(y-k)^{2}=4c(x-h)$
พาราโบลาเปิดซ้าย
จะมีสมการรูปแบบมาตรฐานคือ $(y-k)^{2}=-4c(x-h)$

ตัวอย่างที่ 3 จงจัดรูปสมการพาราโบลา $y^{2}-6y+8x+17=0$ ให้อยู่ในรูปแบบมาตรฐาน

วิธีทำ
จัดสมการพาราโบลาที่กำหนดให้อยู่ในรูปแบบมาตรฐานดังนี้
$y^{2}-6y+9+8x+8=0$
$y^{2}-6y+9=-8x-8$
$(y-3)^{2}=-8(x+1)$
$(y-3)^{2}=-4(2)(x+1)$
จากสมการรูปแบบมาตรฐาน เราจะได้ว่า $k=3,h = -1,c = 2$
พาราโบลานี้เป็นพาราโบลาเปิดซ้ายมีจุดยอดอยู่ที่ $(-1,3)$ , โฟกัสอยู่ที่ $(-3,3)$ และเส้นไดเรกตริกซ์คือ $x = 1$ นั่นเอง

ไฮเพอร์โบลา

บทนิยามไฮเพอร์โบลาจะคล้ายกับบทนิยามของวงรี ต่างกันแค่วงรีใช้ผลบวกของระยะทางจากโฟกัสทั้งสองแต่ว่าไฮเพอร์โบลาจะใช้ผลต่างนั่นเอง

ไฮเพอร์โบลา คือ เซตของจุดทั้งหมดในระนาบซึ่งผลต่างของระยะทางจากจุดใด ๆ ไปยังจุดที่ตรึงอยู่กับที่ทั้งสองจุดมีค่าคงตัว $(2a)$ โดยค่าคงตัวนี้ต้องน้อยกว่าระยะห่างระหว่างจุดคงที่ที่ตรึงอยู่กับที่ทั้งสองจุด เรียกจุดที่ตรึงอยู่กับที่ทั้งสองจุดนี้ว่า โฟกัสของไฮเพอร์โบลา

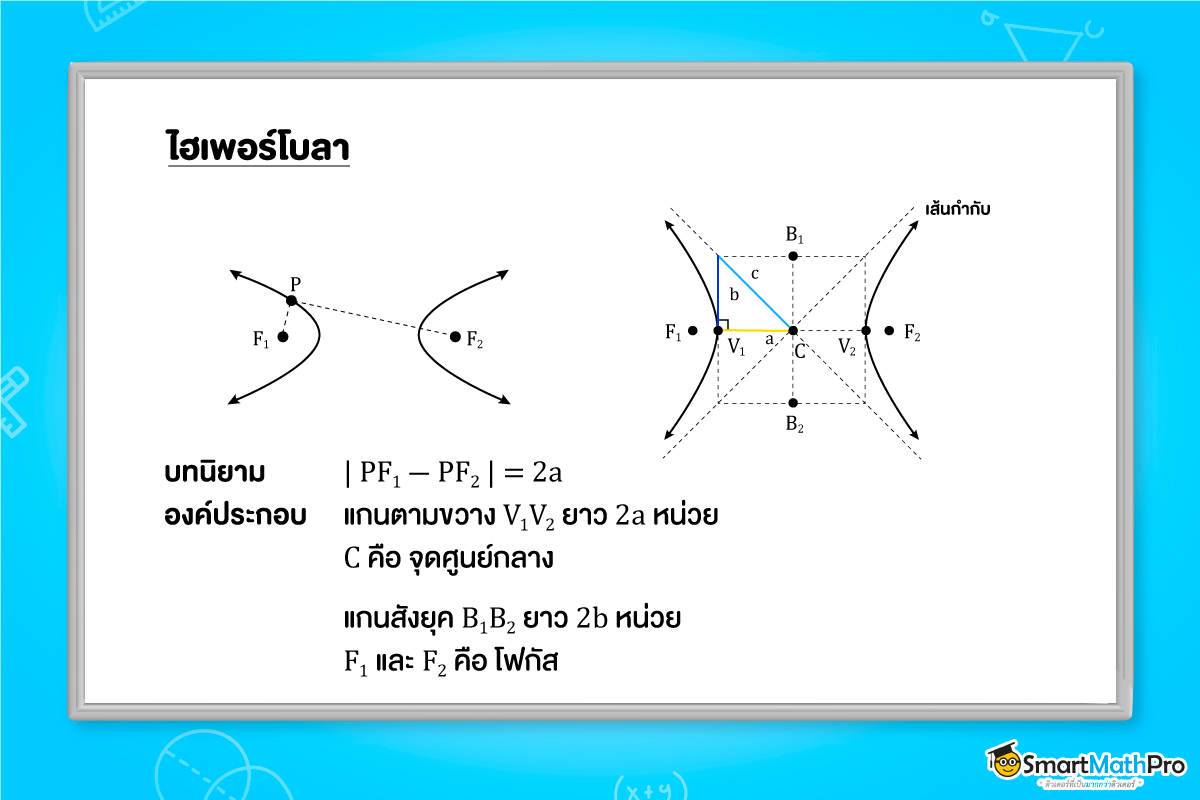
ไฮเพอร์โบลาสามารถวาดได้ 2 แบบตามรูปแบบมาตรฐานของสมการพาราโบลา ซึ่งก็คือ

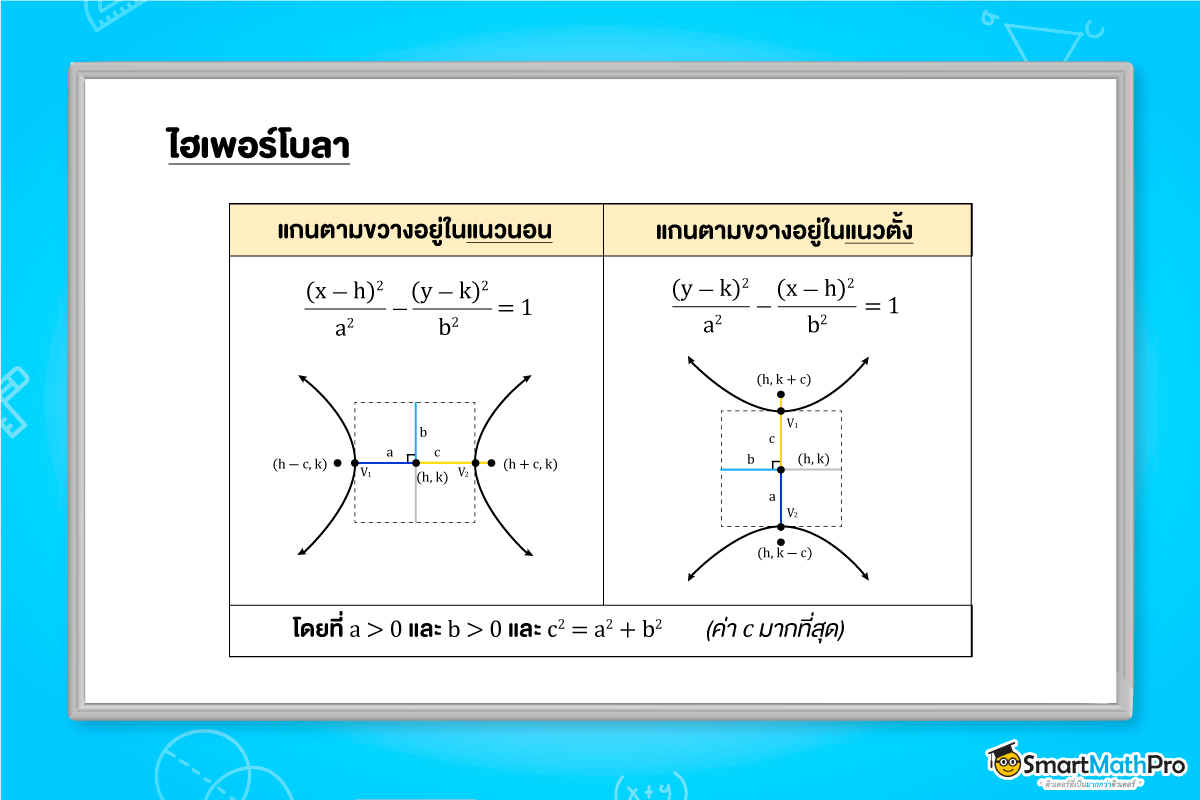
ไฮเพอร์โบลาแกนตามขวางอยู่ในแนวนอน
จะมีสมการรูปแบบมาตรฐานคือ $\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$
ไฮเพอร์โบลาแกนตามขวางอยู่ในแนวตั้ง
จะมีสมการรูปแบบมาตรฐานคือ $\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1$

ตัวอย่างที่ 4 จงจัดรูปสมการไฮเพอร์โบลา $16x^{2}-9y^{2}+160x+72y+112=0$ ให้อยู่ในรูปแบบมาตรฐาน

วิธีทำ
จัดสมการพาราโบลาที่กำหนดให้อยู่ในรูปแบบมาตรฐานดังนี้
$16x^{2}+160x-9y^{2}+72y+112=0$

$16(x^{2}+10x)-9(y^{2}-8y)+112=0$

$16(x^{2}+10x)+16(25)-16(25)-9(y^{2}-8y)-9(16)+9(16)+112=0$

$16(x^{2}+10x+25)-16(25)-9(y^{2}-8y+16)+9(16)+112=0$

$16(x+5)^{2}-9(y-4)^{2}-400+144+112=0$

$16(x+5)^{2}-9(y-4)^{2}=144$

$\frac{16(x+5)^{2}}{144}-\frac{9(y-4)^{2}}{144}=1$

$\frac{(x+5)^{2}}{9}-\frac{(y-4)^{2}}{16}=1$

$\frac{(x+5)^{2}}{3^{2}}-\frac{(y-4)^{2}}{4^{2}}=1$

จากสมการรูปแบบมาตรฐาน เราจะได้ว่า $h=-5,k=4,a=3,b=4,c=5$
ไฮเพอร์โบลานี้เป็นไฮเพอร์โบลาแกนตามขวางอยู่ในแนวนอนที่มีจุดศูนย์กลางอยู่ที่ $(-5,4)$ , จุดยอดอยู่ที่ $(-8, 4)$ และ $(-2,4)$ ส่วนโฟกัสอยู่ที่ $(-10,4)$ และ $(0,4)$

ดูคลิปติวฟรี เรขาคณิตวิเคราะห์และภาคตัดกรวย ม.4

คลิปติว เรขาคณิตวิเคราะห์และภาคตัดกรวย ม.4 จาก SmartMathPro

เรขาคณิตวิเคราะห์และภาคตัดกรวย - Part 1/3

เรขาคณิตวิเคราะห์และภาคตัดกรวย - Part 2/3

เรขาคณิตวิเคราะห์และภาคตัดกรวย - Part 3/3

ดูคลิปติวฟรีอื่น ๆ ได้ที่ YouTube : SmartMathPro

เป็นยังไงบ้างง สำหรับสรุปเนื้อเรื่อง “เรขาคณิตวิเคราะห์และภาคตัดกรวย” ที่พี่เอามาฝากน้อง ๆ ทุกคนนนน หวังว่าจะช่วยให้น้อง ๆ ม.4 หรือคนที่กำลังเตรียมขึ้น ม.4 ได้เข้าใจเรื่องนี้มากขึ้นน้า ส่วนใครที่กังวลว่าตัวเองอาจจะไม่เข้าใจเนื้อหาในบางบทก็อย่าเพิ่งถอดใจน้าา น้อง ๆ ยังสามารถทบทวนในจุดที่ตัวเองไม่เข้าใจได้ อย่ากดดันตัวเองงง

และถ้าใครรู้สึกว่าอยากได้ตัวช่วย เพราะกลัวว่าอ่านเองแล้วอาจจะไม่เข้าใจมากพอ พี่มีคอร์สคณิต ม.ปลายมาแนะนำด้วย เป็นคอร์สที่พี่สอนเอง โดยพี่จะสอนตั้งแต่ปูพื้นฐาน โดยเนื้อหาอิงตามหลักสูตร สสวท. แถมพี่ยังพาตะลุยโจทย์ตั้งแต่โจทย์ซ้อมมือไปจนถึงข้อสอบแข่งขันเลย นอกจากนี้น้อง ๆ สามารถเลือกแพ็กเองได้ด้วยย (กระซิบว่ามีโปรโมชันลดสูงสุดถึง 35% เลยน้าา) ใครสนใจ คลิก ไปดูรายละเอียดกันเลยย

นอกจากจะทบทวนบทเรียนแล้ว พี่อยากแนะนำให้ทุกคนลองดาวน์โหลดแบบฝึกหัดจากคลังข้อสอบไปฝึกทำด้วยยยเพราะนอกจากจะช่วยทวนเนื้อหา วัดความเข้าใจของตัวเองแล้ว ยังช่วยให้น้อง ๆ ได้ฝึกคิด ฝึกแก้โจทย์หลากหลายแนว ซึ่งจะมีประโยชน์มาก ๆ เลยตอนที่เราไปสอบ ทั้งที่โรงเรียนและสนามสอบอื่นด้วยยย และสุดท้ายนี้พี่ก็ขอเป็นกำลังใจให้น้อง ๆ ทุกคนเลยน้า ใครไม่เข้าใจตรงไหนก็กลับมาอ่านบทความนี้ได้เลยย > <

บทความ แนะนำ

สรุปเนื้อหาจำนวนจริง ม.4 เรียนเรื่องอะไรบ้าง

จำนวนจริง ม.4 สรุปครบม้วนเดียวจบ พร้อมแจกโจทย์จำนวนจริงและวิธีทำ

สรุปเนื้อหาคณิต เซต ม.4 พร้อมแจกฟรีเช็กลิสต์

เซต (Set) คืออะไร สรุปเนื้อหาเซต ม.4 พร้อมโจทย์และเฉลย

ตรรกศาสตร์ ม.4 สรุปครบทุกเนื้อหาพร้อมโจทย์ตรรกศาสตร์และวิธีทำ - SmartMathPro

คณิตศาสตร์ ม.4 เทอม 1,2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม

คณิตศาสตร์ ม.5 เทอม 1 เทอม 2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม

คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?

-คณิต-ม.ปลาย-ม.4-ม.5-ม.6-เรียนเรื่องอะไรบ้าง-_-1536x619-1

คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?

บทความ แนะนำ

คณิตศาสตร์ ม.4 เทอม 1, ม.4 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง ?