
ก่อนที่จะอ่านบทความกันพี่ต้องขอถามก่อนเลยว่า น้อง ๆ คงเคยแก้สมการพหุนามแล้วเจอว่าบางสมการ เช่น
x^2=-1 หาคำตอบไม่ได้ (ในระบบจำนวนจริง) ใช่มั้ย ? เพราะก่อนหน้านี้เราจะสนใจเฉพาะคำตอบที่เป็นจำนวนจริงเท่านั้น
แต่ในบทนี้เราจะมาสนใจคำตอบที่ไม่ใช่จำนวนจริงกันบ้าง โดยเราจะขยายขอบเขตของจำนวนจริงให้ใหญ่ขึ้น แล้วเรียกชื่อใหม่ว่า จำนวนเชิงซ้อน ซึ่งจำนวนเชิงซ้อนนี่แหละจะทำให้เกิดคำตอบของสมการพหุนามที่ไม่ใช่จำนวนจริง ดังนั้นมาทำความรู้จักกับจำนวนเชิงซ้อนให้มากขึ้นกันเลย
สนใจหัวข้อไหน ... กดอ่านเลย
Toggleจำนวนเชิงซ้อน ม.5
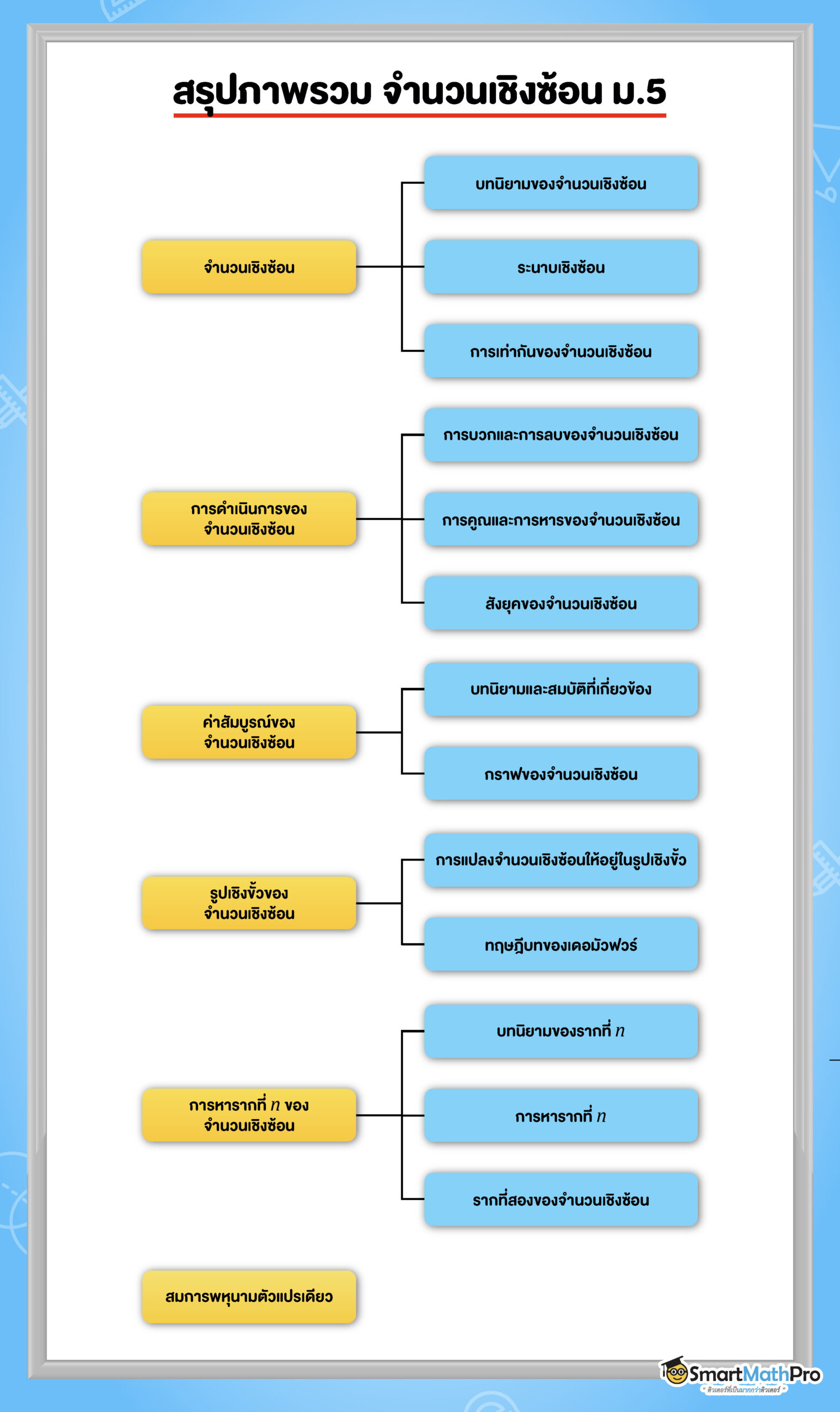
ความหมายของจำนวนเชิงซ้อน
เราจะเขียนแทนเซตของจำนวนเชิงซ้อน (Complex number) ทั้งหมดด้วย \mathbb{C}
บทนิยาม
สำหรับจำนวนเชิงซ้อน z=\left ( a, b \right ) หรือ z=a+bi เมื่อ a และ b เป็นจำนวนจริง
เรียก a ว่า ส่วนจริง (real part) ของ z และเขียนแทนด้วย Re(z)
เรียก b ว่า ส่วนจินตภาพ (imaginary part) ของ z และเขียนแทนด้วย Im(z)
เช่น
- 3+2i
จะได้ว่า 3 คือส่วนจริง และ 2 คือส่วนจินตภาพ หรือสามารถเขียนได้ว่า \left ( 3, 2 \right ) - -2+i
จะได้ว่า -2 คือส่วนจริง และ 1 คือส่วนจินตภาพ หรือสามารถเขียนได้ว่า \left ( -2, 1 \right ) - 5
จะได้ว่า 5 คือส่วนจริง และ 0 คือส่วนจินตภาพ หรือสามารถเขียนได้ว่า \left ( 5, 0 \right ) - -2i
จะได้ว่า 0 คือส่วนจริง และ –2 คือส่วนจินตภาพ หรือสามารถเขียนได้ว่า \left ( 0, -2 \right )
จากบทนิยาม จะได้ว่าจำนวนจริงที่น้อง ๆ เคยเรียน นับว่าเป็นจำนวนเชิงซ้อนที่มีส่วนจินตภาพเป็น 0 และจำนวนเชิงซ้อนที่มีส่วนจริงเป็น 0 แต่ส่วนจินตภาพไม่เป็นศูนย์ เราจะเรียกว่า จำนวนจินตภาพแท้ (purely imaginary number) นั่นเอง
สมบัติเชิงพีชคณิตของจำนวนเชิงซ้อน
หลังจากที่เราได้รู้จักบทนิยามของจำนวนเชิงซ้อนกันไปแล้ว คราวนี้เรามารู้จักสมบัติต่าง ๆ ของจำนวนเชิงซ้อนกันบ้างง มาเริ่มกันที่สมบัติของจำนวนจินตภาพก่อนเลย
สมบัติของจำนวนจินตภาพ i
จากที่เราทราบกันว่า i =\sqrt{-1} เราจะได้ว่า
i =\sqrt{-1}
i^{2} =-1
i^{3} =-1\times i = -i
i^{4} = (i^{2})^{2} = -1^{2} = 1
เราจะได้ว่า i^{4m}=1, i^{4m+1}=i, i^{4m+2}=-1, i^{4m+3}=-i
เมื่อ m\in \mathbb{N}\cup \left \{ 0 \right \}
หรืออธิบายให้เข้าใจง่าย ๆ คือ
- i ยกกำลังด้วยจำนวนที่ 4 หารลงตัว จะมีค่าเท่ากับ 1
- i ยกกำลังด้วยจำนวนที่หารด้วย 4 แล้ว เหลือเศษ 1 จะมีค่าเท่ากับ i
- i ยกกำลังด้วยจำนวนที่หารด้วย 4 แล้ว เหลือเศษ 2 จะมีค่าเท่ากับ -1
- i ยกกำลังด้วยจำนวนที่หารด้วย 4 แล้ว เหลือเศษ 3 จะมีค่าเท่ากับ – i
ตัวอย่างที่ 1 จงหาค่าของ i^{2566} + i^{2023}
วิธีทำ
i^{2566}=i^{4(641)+2}=-1
i^{2023}=i^{4(505)+3}=-i
ดังนั้น i^{2566} + i^{2023}=-1-i
การบวก ลบ คูณ และหารจำนวนเชิงซ้อน
ในระบบจำนวนจริง มีการดำเนินการทั้งบวก ลบ คูณ และหาร ซึ่งในจำนวนเชิงซ้อนก็มีการดำเนินการเช่นเดียวกัน
ในหัวข้อนี้เราจะมาดูกันว่าการดำเนินการของจำนวนเชิงซ้อนเป็นอย่างไร
การบวกและลบจำนวนเชิงซ้อน
การบวกจำนวนเชิงซ้อน
บทนิยาม
ให้ z_{1},z_{2} เป็นจำนวนเชิงซ้อน โดยที่ z_{1}=(a,b) และ z_{2}=(c,d)
หรือ z_{1}=a+bi และ z_{2}=c+di
จะได้ว่า z_{1}+z_{2}=(a,b)+(c,d)=(a+c,b+d)
หรือ z_{1}+z_{2}=(a+c)+(b+d)i
การบวกจำนวนเชิงซ้อน สามารถทำได้โดยการนำส่วนจริงตัวหน้าและส่วนจินตภาพตัวหลังของทั้งสองจำนวนมาบวกกันนั่นเอง
การลบจำนวนเชิงซ้อน
บทนิยาม
ให้ z_{1},z_{2} เป็นจำนวนเชิงซ้อน โดยที่ z_{1}=(a,b) และ z_{2}=(c,d)
หรือ z_{1}=a+bi และ z_{2}=c+di
จะได้ว่า z_{1}-z_{2}=(a,b)-(c,d)=(a-c,b-d)
หรือ z_{1}-z_{2}=(a-c)+(b-d)i
กล่าวได้ว่า การลบจำนวนเชิงซ้อนเป็นการบวกด้วยอินเวอร์สของการบวกนั่นเอง
เช่น กำหนดให้ z_{1}=-1+2i และ z_{2}=3-4i
หาผลบวก จะได้ z_{1}+z_{2}=(-1+3)+(2+(-4))i=2-2i
และหาผลลบ จะได้ z_{1}-z_{2}=(-1-3)+(2-(-4))=-4+6i
การคูณจำนวนเชิงซ้อน
บทนิยาม
ให้ z_{1},z_{2} เป็นจำนวนเชิงซ้อน โดยที่ z_{1}=(a,b) และ z_{2}=(c,d)
หรือ z_{1}=a+bi และ z_{2}=c+di
จะได้ว่า z_{1}z_{2}=(ac-bd,ad+bc)
หรือ z_{1}z_{2}=(ac-bd)+(ad+bc)i
เช่น กำหนดให้ z_{1}=-1+2i และ z_{2}=3-4i
หาผลคูณ จะได้ z_{1}z_{2}=((-1)3-2(-4))+((-1)(-4)+2\cdot 3)i=(-3+6)+(4+6)i=3+10i
สมบัติการบวกและการคูณของจำนวนเชิงซ้อน
กำหนดให้ z,z_{1},z_{2},z_{3} เป็นจำนวนเชิงซ้อน

การหารจำนวนเชิงซ้อน
บทนิยาม
สำหรับจำนวนเชิงซ้อน z และ w ซึ่ง w\neq 0 จะได้ว่า z\div w=zw^{-1} และเขียนแทน z\div w ด้วย \frac{z}{w}
จะเห็นว่าจากบทนิยาม การหารจำนวนเชิงซ้อน คือ การคูณด้วยตัวผกผันการคูณของจำนวนเชิงซ้อนที่เป็นตัวหารนั่นเอง และเพื่อให้เข้าใจมากขึ้นลองไปดูตัวอย่างต่อไปนี้กันน
ตัวอย่างที่ 2 จงหา \frac{3+2i}{4+3i}
วิธีทำ
จากบทนิยาม จะได้ว่า \frac{z}{w}=zw^{-1}
เราจะหาตัวผกผันการคูณ หรืออินเวอร์สการคูณของ 4+3i
จาก z^{-1}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i
จะได้ อินเวอร์สการคูณของ 4+3i คือ \frac{4}{25}-\frac{3}{25}i
ดังนั้น \frac{3+2i}{4+3i}=(3+2i)(\frac{4}{25}-\frac{3}{25}i)
=\frac{12}{25}+\frac{6}{25}+(\frac{8}{25}-\frac{9}{25})i
=\frac{18}{25}-\frac{1}{25}i
สังยุคของจำนวนเชิงซ้อน
หัวข้อนี้คือหัวข้อที่สำคัญและมีทฤษฎีบทที่ช่วยให้เราจัดรูป รวมถึงแก้โจทย์เกี่ยวกับจำนวนเชิงซ้อนได้ง่ายขึ้น
บทนิยามและทฤษฎีบทที่เกี่ยวกับสังยุคของจำนวนเชิงซ้อนจะมีหน้าตาอย่างไร ไปอ่านกันต่อเลยย
บทนิยาม
ให้ z=a+bi เป็นจำนวนเชิงซ้อน สังยุคของ z คือ a-bi
ซึ่งสังยุคของ z จะเขียนด้วย \bar{z} ซึ่ง \bar{z}=\overline{a+bi}=a-bi
เช่น สังยุคของ 7+2i คือ 7-2i
ทฤษฎีบท
ให้ z,z_{1} และ z_{2} เป็นจำนวนเชิงซ้อน จะได้ว่า
1. Re(z)=\frac{1}{2}\left ( z+\bar{z} \right ) และ Im(z)=\frac{1}{2i}\left ( z-\bar{z} \right )
2. \bar{\bar{z}}=z
3. \frac{1}{\bar{z}}=\overline{\left ( \frac{1}{z} \right )} เมื่อ z\neq 0
4. \overline{z_{1}+z_{2}}=\overline{z_{1}}+\overline{z_{2}}
5. \overline{z_{1}-z_{2}}=\overline{z_{1}}-\overline{z_{2}}
6. \overline{z_{1} z_{2}}=\overline{z_{1}}\; \overline{z_{2}}
7. \overline{\left (\frac{z_{1}}{z_{2}} \right )}=\frac{\overline{z_{1}}}{\overline{z_{2}}} เมื่อ z_{2}\neq 0
ตัวอย่างที่ 3 กำหนดให้ z_{1}=2+i และ z_{2}=-3-2i จงเขียน \overline{z_{1}-\overline{z_{2}}} ในรูปของ a+bi เมื่อ a และ b เป็นจำนวนจริง
วิธีทำ
\overline{z_{1}-\overline{z_{2}}}
=\overline{z_{1}}-\overline{\overline{z_{2}}}
=\overline{z_{1}}-z_{2}
= \overline{\left ( 2+i \right )}-(-3-2i)
= 2-i+3+2i
= 5+i
กราฟและค่าสัมบูรณ์ของจำนวนเชิงซ้อน
กราฟของจำนวนเชิงซ้อน
ถ้าน้อง ๆ ยังจำกันได้ จำนวนเชิงซ้อนสามารถเขียนในรูปของคู่อันดับ \left ( a,b \right ) ดังนั้นเราสามารถนำจำนวนเชิงซ้อน \left ( a,b \right ) มาแทนด้วยจุดบนระนาบในระบบพิกัดฉากได้ จะเรียกระนาบนี้ว่า ระนาบเชิงซ้อน โดยเรียกแกน X ว่า แกนจริง เรียกแกน Y ว่า แกนจินตภาพ
ซึ่งการแทนจำนวนเชิงซ้อน \left ( a,b \right ) บนระนาบ สามารถแทนได้ด้วยจุด \left ( a,b \right ) หรือเวกเตอร์ที่มีจุดเริ่มต้นที่จุด \left ( 0,0 \right ) และมีจุดสิ้นสุดที่จุด \left ( a,b \right ) เช่น 4+3i สามารถเขียนบนระนาบเชิงซ้อนได้ ดังนี้
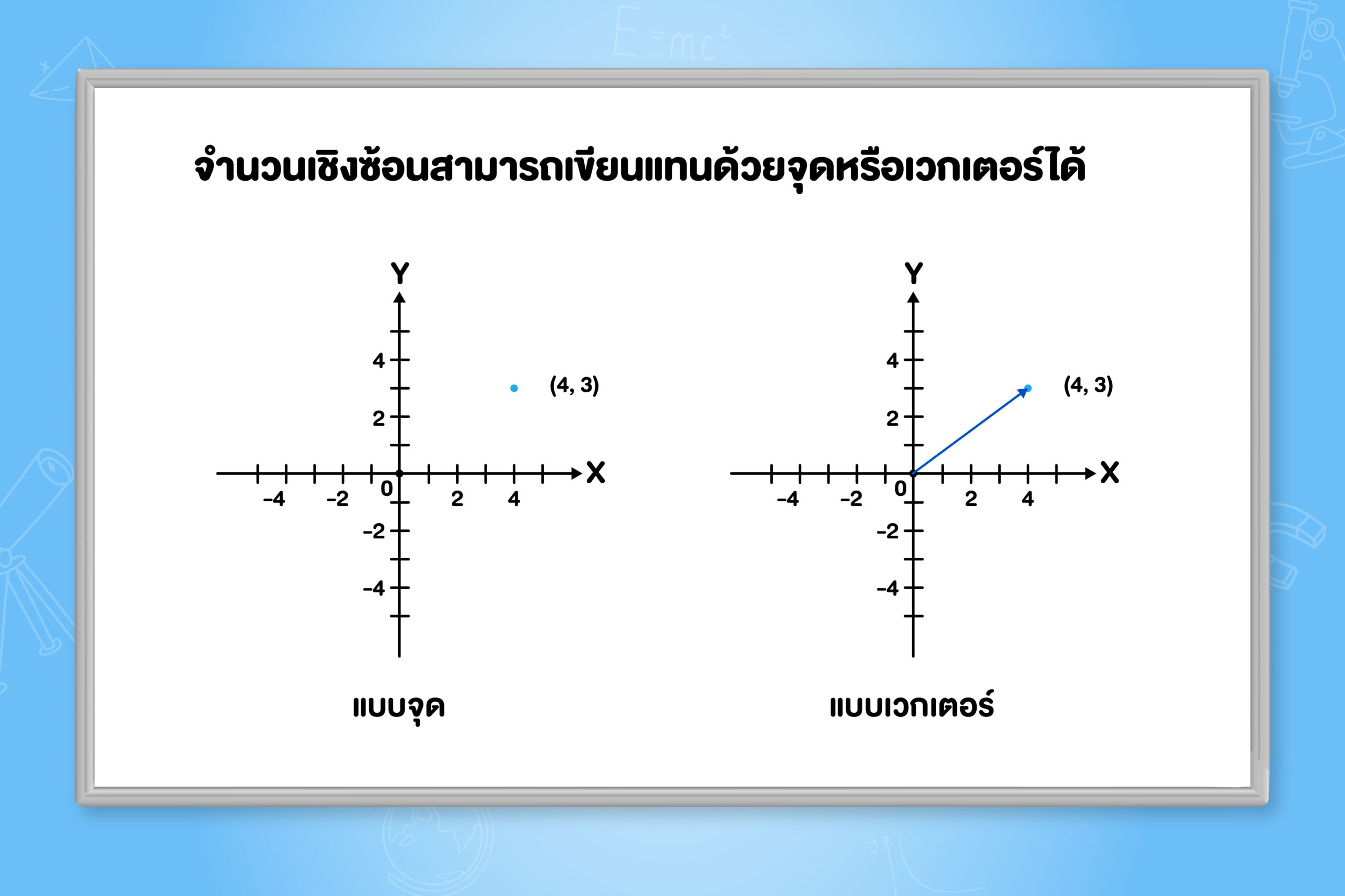
ค่าสัมบูรณ์ของจำนวนเชิงซ้อน
บทนิยาม
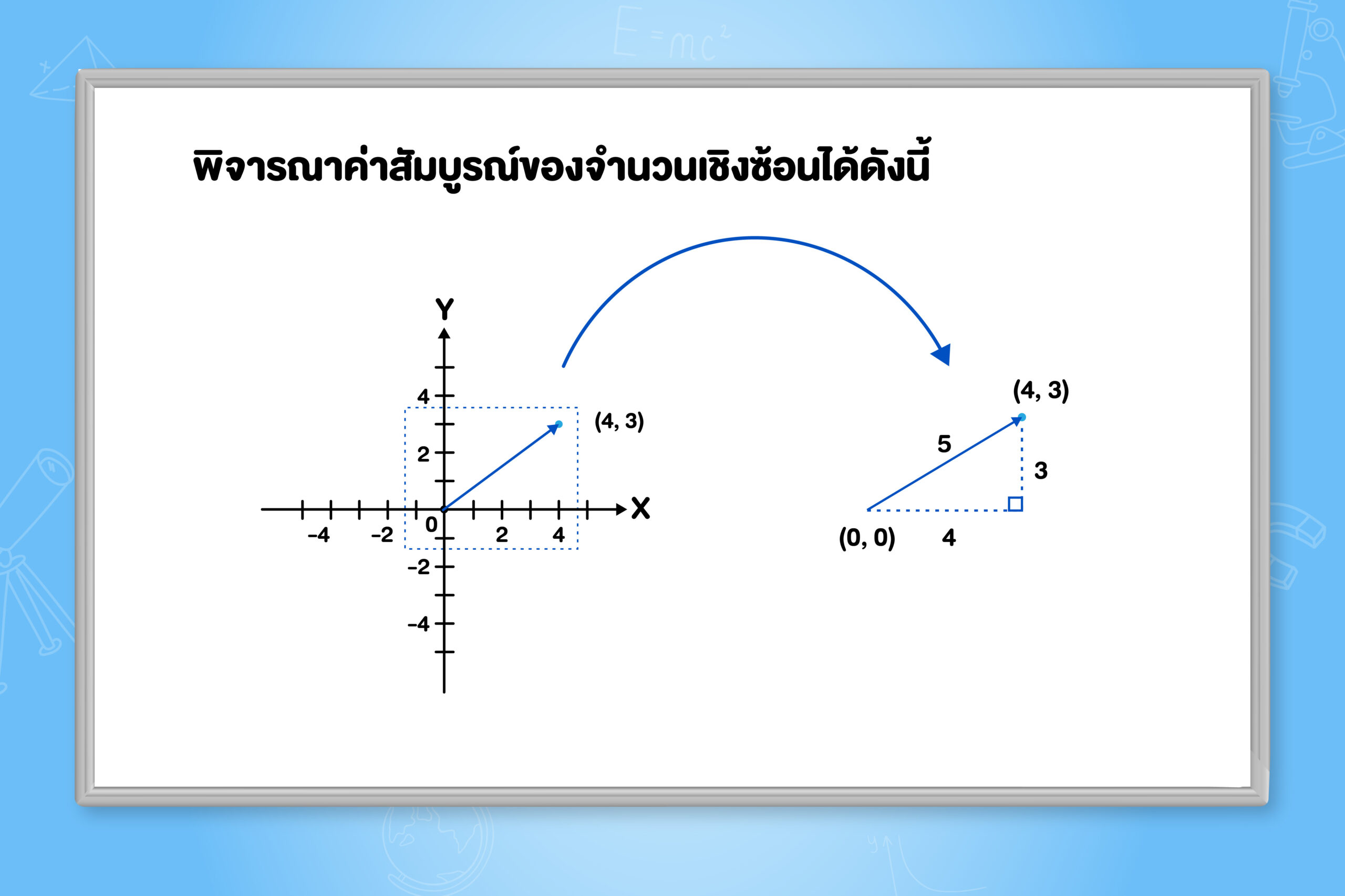
ค่าสัมบูรณ์ (absolute value or modulus) ของจำนวนเชิงซ้อน a+bi คือ จำนวนจริง \sqrt{a^{2}+b^{2}} นั่นคือ \left | a+bi \right |=\sqrt{a^{2}+b^{2}}
จากบทนิยามจะพบว่า ค่าสัมบูรณ์ของจำนวนเชิงซ้อน a+bi คือระยะห่างระหว่างจุด \left ( 0,0 \right ) และจุด \left ( a,b \right ) หรือขนาดของเวกเตอร์ที่มีจุดเริ่มต้นที่จุด \left ( 0,0 \right ) และมีจุดสิ้นสุดที่จุด \left ( a,b \right ) นั่นเอง เช่น ค่าสัมบูรณ์ของ 4+3i คือ 5 นั่นเอง
ทฤษฎีบท
ให้ z,z_{1} และ z_{2} เป็นจำนวนเชิงซ้อน จะได้ว่า
1. \left | z \right |^{2}=z\bar{z}
2. \left | z \right |=\left | -z \right |=\left | \bar{z} \right |
3. \left | \frac{1}{z} \right |=\frac{1}{\left | z \right |} เมื่อ z\neq 0
4. \left | z_{1}z_{2} \right |=\left | z_{1} \right |\left | z_{2} \right |
5. \left | z_{1}+z_{2} \right |\leq \left | z_{1} \right |+\left | z_{2} \right |
6. \left | z_{1}-z_{2} \right |\geq \left | z_{1} \right |-\left | z_{2} \right |
ตัวอย่างที่ 4 กำหนดให้ z_{1}=3-4i และ z_{2}=12+5i ค่าสัมบูรณ์ของจำนวนเชิงซ้อน z_{1}z_{2} เท่ากับเท่าใด
วิธีทำ
\left |z_{1} \right |=\sqrt{3^{2}+(-4)^{2}}=\sqrt{9+16}=5
\left |z_{2} \right |=\sqrt{12^{2}+5^{2}}=\sqrt{144+25}=13
จากทฤษฎีบท \left | z_{1}z_{2} \right |=\left | z_{1} \right |\left | z_{2} \right |
จะได้ว่า \left | z_{1}z_{2} \right |=5\times 13=65
รูปเชิงขั้วของจำนวนเชิงซ้อน
จากที่เราเคยเขียนจำนวนเชิงซ้อน z=x+yi (จำนวนเชิงซ้อนที่ไม่เป็นศูนย์) บนระนาบได้ดังนี้
จากรูป หากเรากำหนดให้ r แทนระยะห่างระหว่างจุดกำเนิด O กับ z
และกำหนดให้ \theta แทนขนาดของมุมที่วัดทวนเข็มนาฬิกาจากแกน X ทางด้านบวก ไปยัง \overrightarrow{Oz} จะได้ความสัมพันธ์ดังนี้
- x=r\cos\theta และ y=r\sin\theta
- r=\left | z \right |=\sqrt{x^2+y^2} และ \tan\theta=\frac{y}{x} เมื่อ x\neq0
ดังนั้นเราจะเขียนจำนวนเชิงซ้อนในอีกรูปหนึ่งได้ดังนี้
จาก z=x+yi เขียนใหม่ได้เป็น z=r\left (\cos\theta +i\sin\theta \right )
โดยเรียก r\left (\cos\theta +i\sin\theta \right ) ว่า รูปเชิงขั้ว (polar form) ของ z และเรียก \theta ว่า อาร์กิวเมนต์ (argument) ของ z
ตัวอย่างที่ 5 จงเขียนจำนวนเชิงซ้อน -1+\sqrt{3}i ให้อยู่ในรูปเชิงขั้ว
วิธีทำ
ขั้นตอนที่ 1 หา r และ \theta
ให้ r\left (\cos\theta +i\sin\theta \right ) เป็นรูปเชิงขั้วของ -1+\sqrt{3}i
จะได้ r=\sqrt{(-1)^2+(\sqrt{3})^2}=\sqrt{1+3}=\sqrt{4}=2
เนื่องจาก \tan\theta =\frac{\sqrt{3}}{-1}=-\sqrt{3} และ \left ( -1, \sqrt{3} \right ) เป็นจุดในจตุภาคที่ 2
จะได้ว่า \theta ค่าหนึ่งที่ทำให้ \tan\theta =-\sqrt{3} คือ \frac{2\pi }{3}
ขั้นตอนที่ 2 นำมาแทนค่าเพื่อหารูปเชิงขั้วของจำนวนเชิงซ้อน
ดังนั้น รูปเชิงขั้วรูปหนึ่งของ -1+\sqrt{3}i คือ 2\left ( \cos\left ( \frac{2\pi }{3} \right )+i\sin\left ( \frac{2\pi }{3} \right ) \right )
น้อง ๆ บางคนอาจรู้สึกว่าการเขียนจำนวนเชิงซ้อนในรูปเชิงขั้วมีความยุ่งยากและซับซ้อนใช่ไหม แต่มันก็มีประโยชน์อยู่น้า การเขียนจำนวนเชิงซ้อนในรูปเชิงขั้วจะช่วยหาผลคูณหรือผลหารได้เร็วขึ้น โดยปกติแล้วถ้าจำนวนเชิงซ้อนในรูปที่ใช้ก่อนหน้านี้จะหาผลคูณโดยการคูณกระจาย หรือหาผลหารโดยใช้สูตรน่ากลัว ๆ
ดังนั้นถ้าเราอยากหาผลคูณหรือผลหารของจำนวนเชิงซ้อน ให้น้อง ๆ ใช้สูตรในทฤษฎีบทด้านล่างนี้ได้เลย
ทฤษฎีบท
ให้ z_1=r_1(\cos\theta_1+i\sin\theta_1) และ z_2=r_2(\cos\theta_2+i\sin\theta_2) โดยที่ z_1\neq0 และ z_2\neq0
- z_1z_2=r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2))
- \frac{z_1}{z_2}=\frac{r_1}{r_2}(\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2))
- \bar{z_1}=r_1(\cos(-\theta_1)+i\sin(-\theta_1))
แล้วถ้าเป็นการยกกำลังล่ะ เราจะหาได้จากอะไร… ไม่ยากเลย น้อง ๆ สามารถใช้ทฤษฎีบทเดอมัวฟวร์มาช่วยหาได้น้าา
ทฤษฎีบทเดอมัวฟวร์ (De Moivre’s Theorem)
ให้ z=r\left (\cos\theta +i\sin\theta \right ) เป็นจำนวนเชิงซ้อนที่ไม่เป็นศูนย์ และ n เป็นจำนวนเต็มบวก
จะได้ว่า z^n=r^n\left (\cos\left (n\theta \right ) +i\sin\left (n\theta \right ) \right )
รากที่ n ของจำนวนเชิงซ้อน
ก่อนจะเริ่มหารากที่ n ของจำนวนเชิงซ้อน น้อง ๆ มาหารากที่สองของจำนวนเชิงซ้อนกันก่อนดีกว่า นั่นคือสูตรด้านล่างนี้
กำหนดจำนวนเชิงซ้อน z=a+bi และให้ r=\sqrt{a^2+b^2} จะได้ว่ารากที่สองของ z คือ
- \pm \left ( \sqrt{\frac{r+a}{2}}+\sqrt{\frac{r-a}{2}}i \right ) เมื่อ b\geq 0
- \pm \left ( \sqrt{\frac{r+a}{2}}-\sqrt{\frac{r-a}{2}}i \right ) เมื่อ b<0
นอกจากสูตรที่พี่เขียนมาข้างต้น เรายังสามารถนำทฤษฎีบทของเดอมัวฟวร์ มาช่วยในการหารากที่ n ของจำนวนเชิงซ้อน เมื่อ n เป็นจำนวนเต็มบวก นั่นหมายความว่าเราสามารถหารากที่ 2 ของจำนวนเชิงซ้อนได้เช่นกัน
ลองค่อย ๆ สังเกตตามพี่น้าา ถ้าเราให้ w เป็นจำนวนเชิงซ้อน และ n เป็นจำนวนเต็มบวก เราจะได้ว่ารากที่ n ของ w คือ จำนวนเชิงซ้อน z ที่สอดคล้องกับ z^n=w
พี่จะขอยกตัวอย่างเพิ่มเติม เช่น \frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i เป็นรากที่ 4 ของ 1 เพราะว่า \left (\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i \right )^{4}=1
เราจะใช้ทฤษฎีบทต่อไปนี้ในการหารากที่ n ของจำนวนเชิงซ้อน
ถ้า w=r\left ( \cos\theta +i\sin\theta \right ) เป็นจำนวนเชิงซ้อนที่ไม่เป็นศูนย์ แล้ว
รากที่ n ของ w มีทั้งหมด n รากที่แตกต่างกัน คือ z=\sqrt[n]{r}\left ( \cos\left (\frac{\theta +2k\pi }{n} \right ) +i\sin\left (\frac{\theta +2k\pi }{n} \right ) \right ) เมื่อ k\in \left \{ 0, 1, 2, … , n-1 \right \}
ตัวอย่างที่ 6 จงหารากที่ 4 ของ 2+2\sqrt{3}i
วิธีทำ
กำหนดให้ w=2+2\sqrt{3}i
ดังนั้น เขียนจำนวนเชิงซ้อน w ให้อยู่ในรูปเชิงขั้วได้ว่า 4\left ( \cos\frac{\pi }{3}+i\sin\frac{\pi}{3} \right )
และกำหนดให้ z=r\left (\cos\theta +i\sin\theta \right ) เป็นรากที่สี่ของ w
จะได้ z^4=2+2\sqrt{3}i
จากทฤษฎีบทของเดอมัวฟวร์ จะได้ z^4=r^4\left ( \cos4\theta +i\sin4\theta \right )=4\left ( \cos\frac{\pi }{3}+i\sin\frac{\pi}{3} \right )
ดังนั้น r^4=4
จะได้ว่า r=\sqrt[4]{4}=\sqrt{2}
และ 4\theta-\frac{\pi}{3}=2k\pi เมื่อ k\in \mathbb{Z}
จะได้ว่า \theta = \frac{\frac{\pi}{3}+2k\pi}{4} เมื่อ k\in \mathbb{Z}
ดังนั้น z=\sqrt{2}\left ( \cos\left (\frac{\pi}{12}+\frac{k\pi}{2} \right ) +i\sin\left (\frac{\pi}{12}+\frac{k\pi}{2} \right ) \right ) เมื่อ k\in \mathbb{Z}
เมื่อ k=0 จะได้ z_1=\sqrt{2}\left (\cos\frac{\pi}{12}+i\sin\frac{\pi}{12} \right )
เมื่อ k=1 จะได้ z_2=\sqrt{2}\left (\cos\frac{7\pi}{12}+i\sin\frac{7\pi}{12} \right )
เมื่อ k=2 จะได้ z_3=\sqrt{2}\left (\cos\frac{13\pi}{12}+i\sin\frac{13\pi}{12} \right )
เมื่อ k=3 จะได้ z_4=\sqrt{2}\left (\cos\frac{19\pi}{12}+i\sin\frac{19\pi}{12} \right )
สมการพหุนามตัวแปรเดียว
หน้าตาของสมการพหุนามตัวแปรเดียวในหัวข้อนี้จะคล้ายกับที่น้อง ๆ เคยเจอมาเลย แต่ในหัวข้อนี้เราจะเจอคำตอบของสมการที่เป็นจำนวนเชิงซ้อนด้วย ดังนั้นเราจะต้องใช้ความรู้เดิมมาช่วยแก้สมการด้วย
พหุนาม p(x) มี x-c เป็นตัวประกอบ ก็ต่อเมื่อ p(c)=0
ต่อมาพี่จะพูดถึงจำนวนคำตอบของสมการพหุนามตัวแปรเดียว หลังจากที่เราแก้สมการพหุนามตัวแปรเดียวแล้ว จำนวนคำตอบของสมการจะเป็นดังต่อไปนี้เลย
ให้ p(x) เป็นพหุนามที่มีสัมประสิทธิ์เป็นจำนวนจริงและมีดีกรี n เมื่อ n\geq 0 จะได้ว่าสมการ p(x)=0 จะมีคำตอบทั้งหมด n คำตอบ เมื่อนับคำตอบที่ซ้ำกัน
ที่สำคัญที่สุดเลยคือทฤษฎีบทในกรอบต่อไปนี้ จะกล่าวถึงคำตอบของสมการพหุนามตัวแปรเดียวที่เป็นจำนวนเชิงซ้อนถ้าเรารู้คำตอบที่เป็นจำนวนเชิงซ้อนตัวหนึ่งแล้ว เราจะสามารถหาคำตอบอีกตัวหนึ่งได้เลยโดยใช้ทฤษฎีบทนี้
ถ้าจำนวนเชิงซ้อน z เป็นคำตอบของสมการพหุนามกำลัง n โดยที่สัมประสิทธิ์ทุกตัวเป็นจำนวนจริง แล้ว \bar{z} จะเป็นคำตอบของสมการพหุนามนี้ด้วย
เช่น กำหนดสมการ x^2-4x+13=0 มี 2+3i เป็นคำตอบตัวหนึ่งของสมการ
จะได้ว่า 2-3i เป็นคำตอบอีกตัวหนึ่งของสมการด้วย
ตัวอย่างที่ 7 จงหาสมการพหุนามดีกรี 3 ที่มีสัมประสิทธิ์เป็นจำนวนเต็ม มี 2 และ 3-i เป็นคำตอบ และมีสัมประสิทธิ์นำเป็น 1
วิธีทำ
เนื่องจาก 3-i เป็นคำตอบของสมการ จะได้ว่า 3+i เป็นคำตอบของสมการด้วย
จะได้
(x-2)(x-(3-i))(x-(3+i))=0
(x-2)(x-3+i)(x-3-i)=0
(x-2)(x^2-6x+10)=0
x^3-8x^2+22x-20=0
ข้อสอบคณิตพร้อมเฉลย
ดูคลิปติวคณิต ม.5 เทอม 1 และ 2
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
จำนวนเชิงซ้อน ม.5 เป็นอีกหนึ่งบทในเนื้อหาคณิตศาสตร์ ม.5 ที่มีทั้งทฤษฎีบท ตัวแปร สูตร และการเขียนกราฟที่
ค่อนข้างเยอะประมาณหนึ่งเลย ทำให้หลายคนก็อาจจะรู้สึกงงอยู่บ้างเมื่อเรียนเนื้อหาเรื่องนี้ แต่พี่แนะนำว่าให้ค่อย ๆ ทำความเข้าใจและฝึกทำโจทย์ควบคู่ไปด้วยน้าา จะยิ่งทำให้เข้าใจมากขึ้น พร้อมไปสอบกลางภาคแน่นอนน
ซึ่งถ้าใครอยากได้โจทย์คณิตศาสตร์ ม.ปลาย ไว้ซ้อมมือ พี่ก็มีแบบฝึกหัดใน คลังข้อสอบ ให้ทุกคนได้ฝึกทำอีกเพียบเลยย เข้าไปดาวน์โหลดกันได้น้าา
เนื้อหาคณิตศาสตร์ ม.ปลาย อาจดูเป็นเรื่องยากในความคิดของน้อง ๆ หลายคน แต่ที่จริงถ้าเรามีพื้นฐานที่ดี ทบทวนบทเรียนและฝึกทำโจทย์บ่อย ๆ ก็จะทำให้เข้าใจในเนื้อหามากขึ้น แต่ถ้าใครยังกังวล กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากได้คนช่วยไกด์
พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
บทความ แนะนำ

ทีมวิชาการคณิตศาสตร์
ผู้อยู่เบื้องหลังการจัดทำคอร์สเรียนร่วมกับพี่ติวเตอร์
และผู้เขียนบทความวิชาการคณิตศาสตร์ของสถาบัน SmartMathPro

ทีมวิชาการคณิตศาสตร์
ผู้อยู่เบื้องหลังการจัดทำคอร์สเรียนร่วมกับพี่ติวเตอร์
และผู้เขียนบทความวิชาการคณิตศาสตร์ของสถาบัน SmartMathPro
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro





















