หลังจากเรียนจบเทอม 1 กันไปแล้ว มีใครรู้สึกกังวลกับคณิต ม.ปลายบ้าง ? แน่นอนว่ายิ่งเรียนปีสูงขึ้นเท่าไหร่ เนื้อหามันก็ต้องยากขึ้นเรื่อย ๆ ใช่มั้ยย อาจจะทำให้หลายคนกังวลและกลัวว่าจะไม่เข้าใจในบางบทเรียน แต่ความเครียดนั้นจะหายไป เพราะพี่ ๆ ได้เตรียมสรุปคณิตศาสตร์มาให้ทุกคนได้อ่านก่อนสอบแล้ววว
ซึ่งบทเรียนที่พี่ ๆ เตรียมมาในวันนี้ก็เป็นหนึ่งในบทเรียนของคณิต ม.4 เทอม 2 อย่างเรื่อง ความสัมพันธ์และฟังก์ชัน
ใครที่ไม่เข้าใจเรื่องนี้ หรืออยากจะเตรียมตัวล่วงหน้า ควรอ่านบทความนี้น้าเพราะนอกจากจะสรุปเนื้อหาแล้ว ยังมีคลิป
ติวฟรีพร้อมโจทย์ให้ฝึกทำอีกด้วย !!
“ความสัมพันธ์” เป็นคำที่เราใช้กันบ่อยมาก เช่น ความสัมพันธ์แบบเพื่อน แฟน Friend Zone หรือ แม้กระทั่งความสัมพันธ์ระหว่างสิ่งของกับสิ่งของก็ตาม อย่างไรก็ตาม นักคณิตศาสตร์อยากลองนิยามคำว่า “ความสัมพันธ์” ให้ชัดเจนว่ามันมีหน้าตาเป็นอย่างไร มา !!! เดี๋ยวเราลองไปดูกันเลยยยย
ผลคูณคาร์ทีเซียน
บทนิยาม
ผลคูณคาร์ทีเซียนของเซต A และเซต B คือเซตของคู่อันดับ katex is not defined ทั้งหมด
โดยที่ katex is not defined เป็นสมาชิกของเซต A และ katex is not defined เป็นสมาชิกของเซต B
สามารถเขียนผลคูณคาร์ทีเซียนของเซต A และเซต B แทนด้วย katex is not defined
เช่น กำหนดให้ katex is not defined และ katex is not defined
ดังนั้น katex is not defined
ความสัมพันธ์
บทนิยาม
r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ katex is not defined
เช่น กำหนดให้ katex is not defined และ katex is not defined
ถ้า katex is not defined จะสามารถเขียนแจกแจงสมาชิกได้ดังนี้ katex is not defined
หรือเราสามารถเรียกได้ว่า katex is not defined เป็นความสัมพันธ์ “น้อยกว่า” จาก A ไป B นั่นเอง
กราฟของความสัมพันธ์
ในหัวข้อนี้เราจะสนใจเฉพาะความสัมพันธ์ของจำนวนเท่านั้นนะ โดยเราสามารถนำความสัมพันธ์มาแสดงเป็นภาพได้โดยนำคู่อันดับในความสัมพันธ์มาแสดงเป็นพิกัดของจุดแล้ววางลงไปบนระนาบ XY ก็จะได้ออกมาเป็นกราฟของ
ความสัมพันธ์ต่าง ๆ
กราฟของความสัมพันธ์ r มีอยู่ 3 ลักษณะ
- กราฟมีลักษณะเป็นจุด
เช่น katex is not defined เป็นสมาชิกของ katex is not defined ดังรูป - กราฟมีลักษณะเป็นเส้น
เช่น katex is not defined เป็นสมาชิกของ katex is not defined มีเงื่อนไขเป็นสมการ ดังรูป - กราฟมีลักษณะเป็นพื้นที่
เช่น katex is not defined เป็นสมาชิกของ katex is not defined มีเงื่อนไขเป็นอสมการ
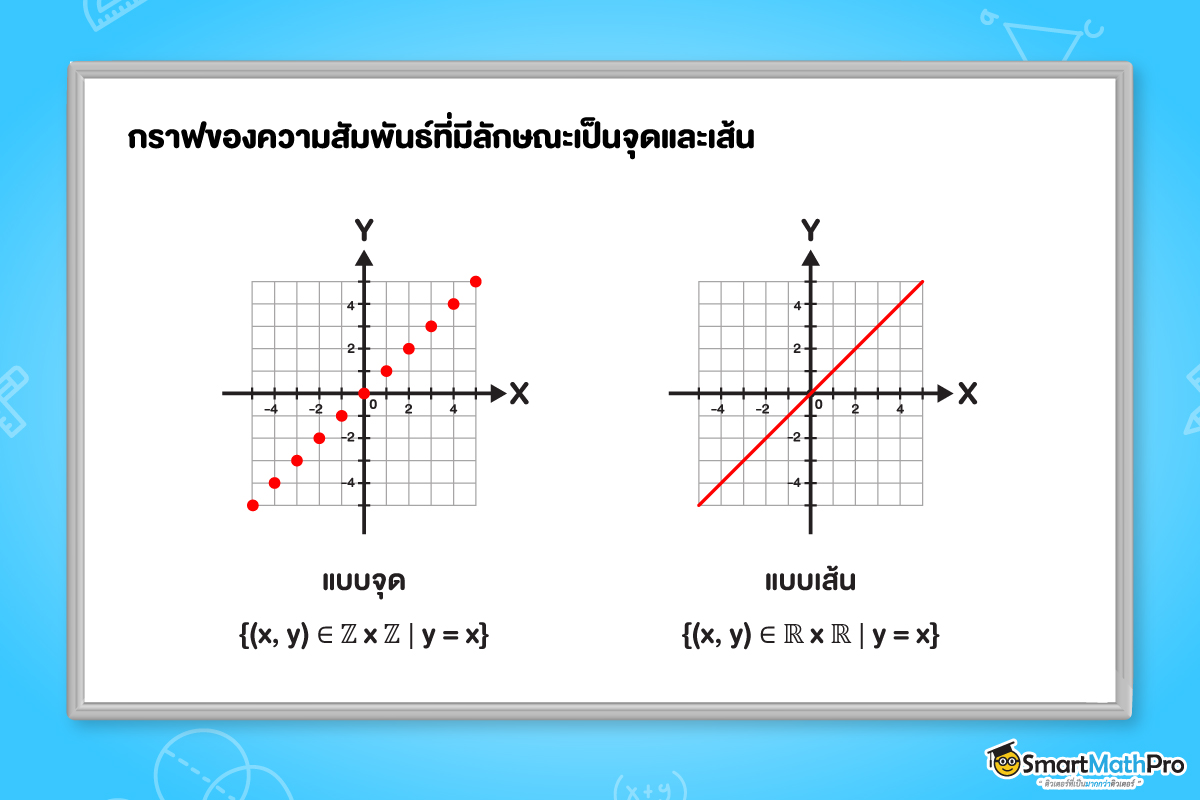
ข้อสังเกต
เรานำสมาชิกตัวหน้ามาเป็นค่าตำแหน่งบนแกน X และนำสมาชิกตัวหลังเป็นค่าตำแหน่งบนแกน Y แล้วใช้ค่าตำแหน่ง
ทั้งสองมาเป็นพิกัดในการลงจุดเพื่อวาดกราฟนั่นเอง
โดเมนและเรนจ์ของความสัมพันธ์
คราวนี้ก็มาถึงหัวข้อที่สำคัญมาก ๆ และน้อง ๆ ทุกคนจะได้เจอในข้อสอบอย่างแน่นอนนั่น คือ โดเมนและเรนจ์ของความสัมพันธ์ ซึ่งเราจะต้องหาทั้งในรูปแบบของเซตและกราฟได้ ดังนั้นเรามาทำความรู้จักกับบทนิยามของโดเมนและเรนจ์กันก่อนเลย
บทนิยาม
ให้ r เป็นความสัมพันธ์จาก A ไป B
- โดเมนของ r คือ เซตของสมาชิกตัวหน้าของคู่อันดับทั้งหมดใน r เขียนแทนด้วย katex is not defined
- เรนจ์ของ r คือ เซตของสมาชิกตัวหลังของคู่อันดับทั้งหมดใน r เขียนแทนด้วย katex is not defined
ตัวอย่างที่ 1 จงหาโดเมนและเรนจ์จากกราฟของความสัมพันธ์ที่กำหนดให้ต่อไปนี้
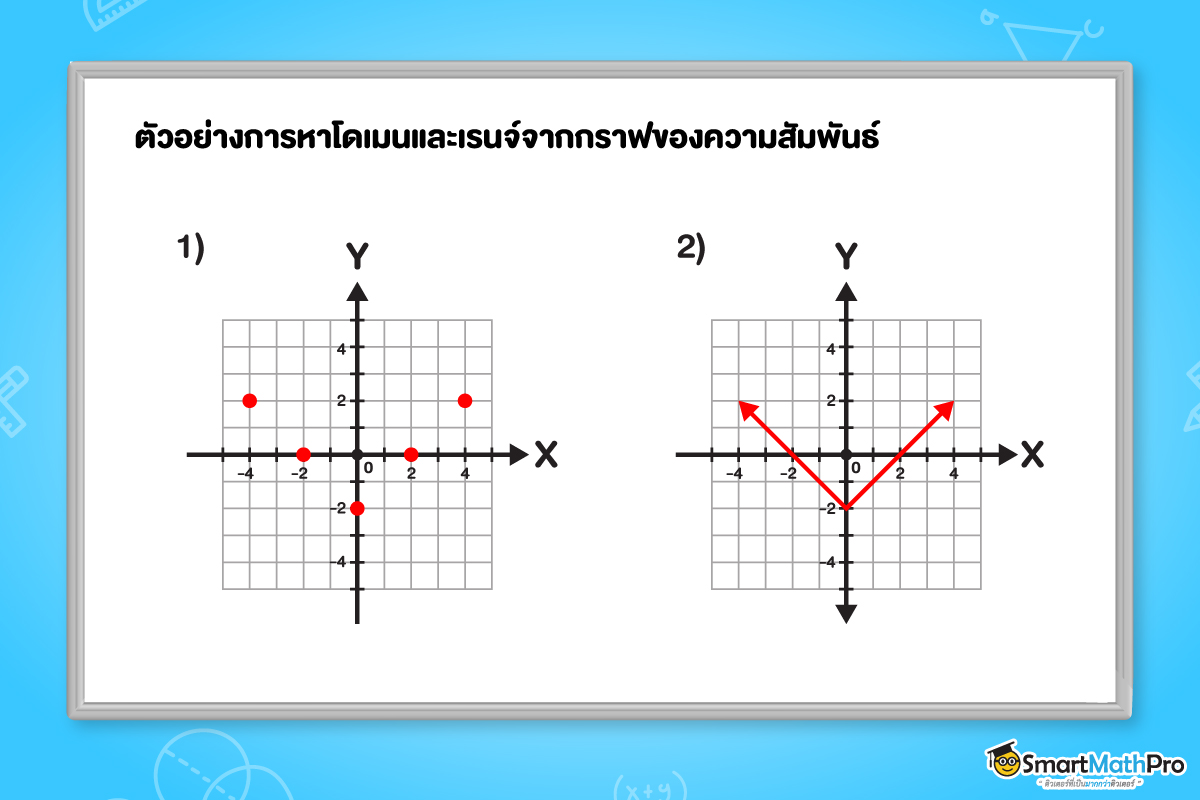
วิธีทำ
จากข้อ 1)
กำหนดให้เป็นกราฟของความสัมพันธ์ katex is not defined
จะได้ว่า katex is not defined
ดังนั้น katex is not defined และ katex is not defined
จากข้อ 2)
แนวคิด เราสามารถมองเส้นจากกราฟของความสัมพันธ์ katex is not defined ได้ว่าเป็นจุดจำนวนมากเรียงต่อกัน จนกลายเป็นเส้น ดังนั้น วิธีการหาโดเมนและเรนจ์จากกราฟในข้อนี้ สามารถมองได้ด้วยวิธีคล้ายกับกับข้อ 1)
สมาชิกตัวหน้าของคู่อันดับจะเป็นจำนวนจริงทั้งหมดเลย (ตั้งแต่ katex is not defined จนถึง katex is not defined)
ถ้าเริ่มมองจากแกน Y ด้านล่างขึ้นมา จะเห็นว่าสมาชิกตัวหลังของคู่อันดับจะเป็นจำนวนตั้งแต่ -2 จนถึง katex is not defined
จะได้ว่า katex is not defined และ katex is not defined
จากตัวอย่างก่อนหน้า เราสามารถสรุปการหาโดเมนและเรนจ์จากกราฟของความสัมพันธ์ได้เป็นดังนี้เลยย
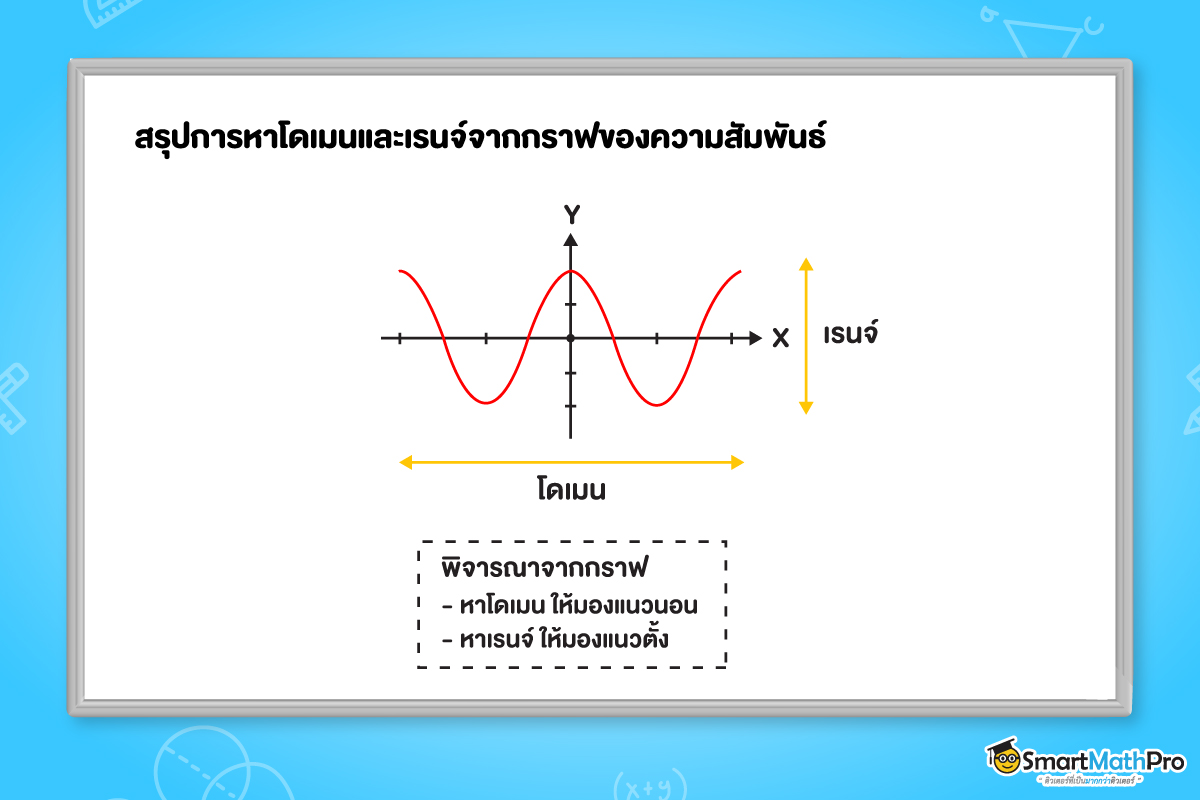
นอกจากการหาโดเมนและเรนจ์จากกราฟของความสัมพันธ์แล้ว ถ้าโจทย์ให้ความสัมพันธ์ที่เขียนในรูปของเซตแบบบอกเงื่อนไข เราจะใช้เทคนิคในการพิจารณาเงื่อนไขแล้วหาโดเมนและเรนจ์ของความสัมพันธ์ ซึ่งจะมีขั้นตอนดังต่อไปนี้
เทคนิค การหาโดเมนและเรนจ์ด้วยวิธีพิจารณาจากเงื่อนไข
ให้พิจารณาเงื่อนไขดังนี้
- katex is not defined
จะได้ว่า katex is not defined (ตัวส่วนไม่เท่ากับศูนย์) - katex is not defined (เมื่อ n เป็นจำนวนคู่)
จะได้ว่า katex is not defined และ katex is not defined
ตัวอย่างที่ 2 จงหาโดเมนและเรนจ์ของความสัมพันธ์ต่อไปนี้
1) katex is not defined
วิธีทำ
พิจารณา katex is not defined จะเห็นว่า katex is not defined ต้องไม่เป็นศูนย์
นั่นคือ katex is not defined
ดังนั้น katex is not defined
พิจารณา katex is not defined
จะได้ว่า katex is not defined
ดังนั้น katex is not defined
2) katex is not defined
วิธีทำ
พิจารณา katex is not defined
จะได้ว่า x ต้องไม่เป็นจำนวนลบ
ดังนั้น katex is not defined
เนื่องจาก x ไม่เป็นจำนวนลบ แล้วแทน x ด้วย 0 ใน katex is not defined จะได้ค่าที่น้อยที่สุดเท่ากับ 0
ดังนั้น katex is not defined
ตัวผกผันของความสัมพันธ์
บทนิยาม
ตัวผกผันของความสัมพันธ์ r คือความสัมพันธ์ที่เกิดจากการสลับที่ของสมาชิกตัวหน้า และสมาชิกตัวหลัง
ในแต่ละคู่อันดับที่เป็นสมาชิกของ r
ตัวผกผันของความสัมพันธ์ r เขียนแทนด้วย katex is not defined
เช่น ถ้า katex is not defined แล้วจะได้ว่า katex is not defined
ก่อนหน้านี้เราเคยเขียนความสัมพันธ์ให้อยู่ในรูปเซตแบบบอกเงื่อนไข ดังนั้นเราก็สามารถเขียนตัวผกผันของความสัมพันธ์ให้อยู่ในรูปของเซตแบบบอกเงื่อนไขได้เช่นกัน
เช่น
แบบที่ 1: katex is not defined หรือ
แบบที่ 2: katex is not defined
ซึ่งถ้าน้อง ๆ ลองสังเกตจะเห็นว่าการเขียนทั้งสองแบบเกิดจากการสลับ x และ y แต่แบบที่ 1 จะสลับที่ด้านหน้าเพียง
อย่างเดียว ส่วนแบบที่ 2 จะสลับที่เพียงด้านหลังอย่างเดียวเท่านั้น ถ้าใครเผลอไปเขียนตัวผกผันของความสัมพันธ์แล้วสลับทั้งสองที่จะผิดได้นะ !
ฟังก์ชัน
หลังจากที่เรารู้จักความสัมพันธ์กันไปแล้ว มันก็จะมีความสัมพันธ์บางอย่างที่เราได้ให้ชื่อมันเอาไว้ ซึ่งความสัมพันธ์ประเภทนี้จะเป็นพื้นฐานสำคัญที่นำไปต่อยอดในหัวข้ออื่น ๆ ได้อีกมากมาย ความสัมพันธ์นี้มีชื่อว่า “ฟังก์ชัน”
ความหมายของฟังก์ชัน
บทนิยาม
ฟังก์ชัน คือ ความสัมพันธ์ที่คู่อันดับสองคู่อันดับใด ๆ ของความสัมพันธ์นั้น ถ้ามีสมาชิกตัวหน้าเหมือนกันแล้ว สมาชิกตัวหลังต้องเหมือนกัน
จากบทนิยามข้างต้น พี่จะขออธิบายง่าย ๆ แบบนี้น้าา ฟังก์ชัน คือ ความสัมพันธ์ที่สมาชิกตัวหน้าแต่ละตัวจะจับกับสมาชิกตัวหลังเพียงค่าเดียวเท่านั้น !!
ฟังก์ชันโดยส่วนใหญ่มักจะเขียนแสดงได้ 3 รูปแบบคือ แผนภาพ เซต และกราฟของฟังก์ชัน โดยกราฟของฟังก์ชันจะถูก
ใช้บ่อยและมีความสำคัญมากกก พี่เลยจะขอยกให้เป็นหัวข้อใหญ่หลังจากพี่อธิบายการเขียนฟังก์ชันสองแบบแรกน้าา
1. เขียนในรูปของแผนภาพ
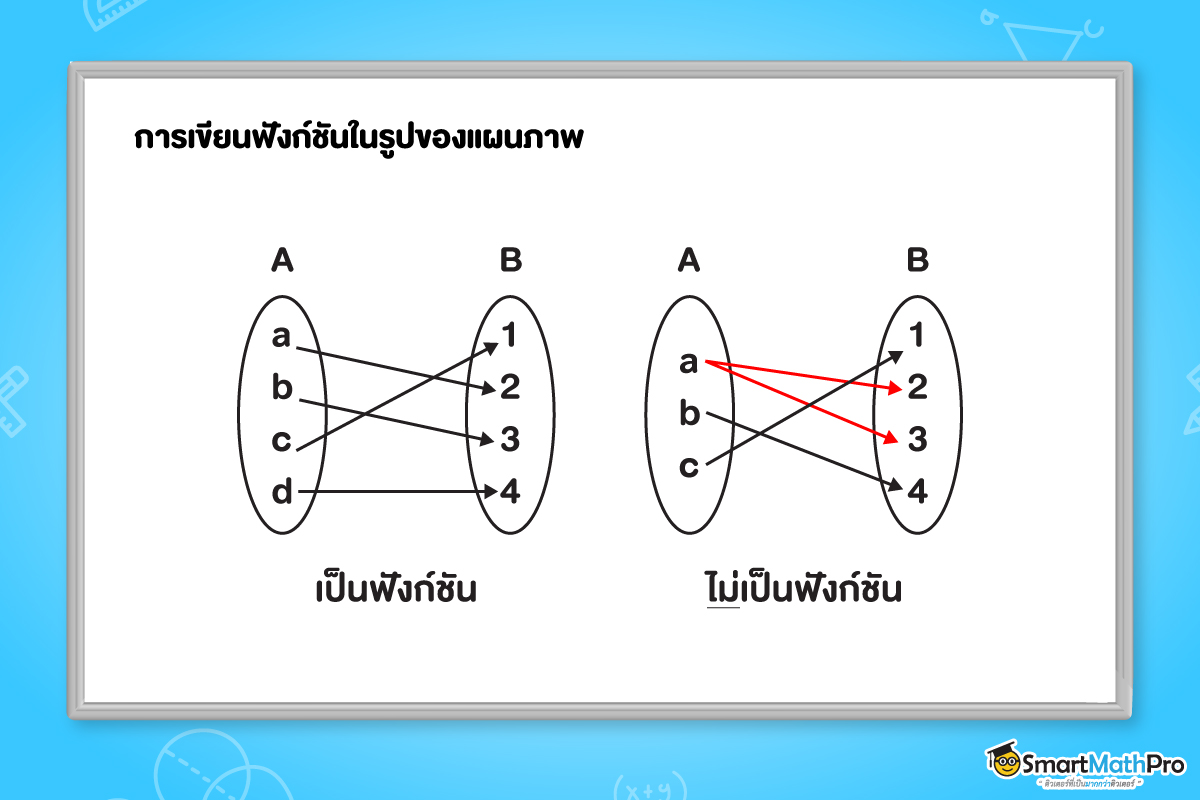
2. เขียนในรูปของเซต
สามารถเขียนได้ 2 แบบ คือ แบบแจกแจงสมาชิกตรง ๆ และ แบบบอกเงื่อนไข เช่น
แบบแจกแจงสมาชิก
- katex is not defined
แบบบอกเงื่อนไข
- katex is not defined
ตัวอย่างที่ 3 กำหนดให้ katex is not defined จงพิจารณาความสัมพันธ์ต่อไปนี้ว่าเป็นฟังก์ชันหรือไม่
1. katex is not defined
วิธีทำ
จาก f เมื่อเขียนความสัมพันธ์แบบแจกแจงสมาชิกจะได้
katex is not defined
สังเกตว่า สมาชิกของแต่ละตัวใน f ไม่มีคู่อันดับตัวไหนเลยที่ “ถ้าเลขตัวหน้าในคู่อันดับซ้ำกันแล้วตัวหลังไม่ซ้ำกัน”
ดังนั้น f เป็นฟังก์ชัน
2. katex is not defined
วิธีทำ
จาก g เมื่อเขียนความสัมพันธ์แบบแจกแจงสมาชิกจะได้
katex is not defined
สังเกตว่า g มีคู่อันดับ katex is not defined และ katex is not defined มีเลขตัวหน้าในคู่อันดับซ้ำกันคือ เลข 1 และมีตัวหลังต่างกันคือ 1 และ -1
ดังนั้น g ไม่เป็นฟังก์ชัน
กราฟของฟังก์ชัน
ตัวอย่างที่ 4 จงพิจารณาว่ากราฟต่อไปนี้เป็นฟังก์ชันหรือไม่
1.
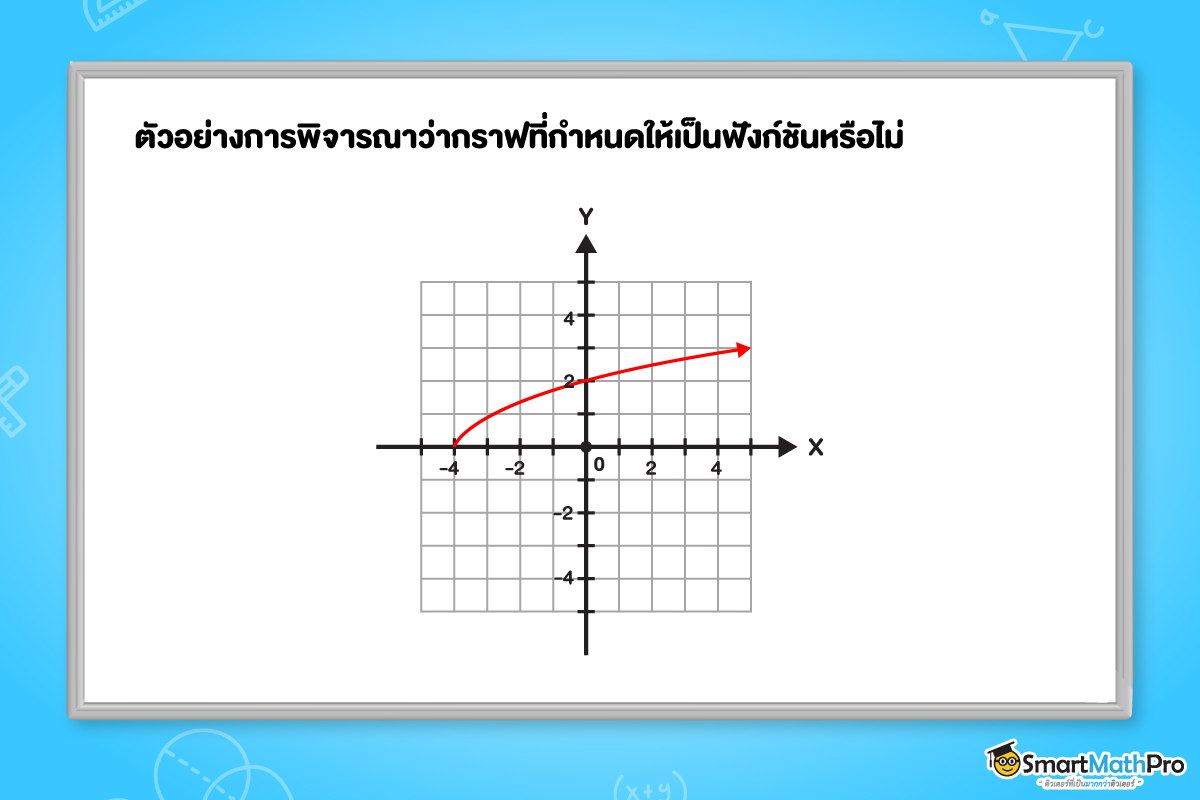
วิธีทำ
ลากเส้นตรงในแนวตั้ง (ขนานแกน Y) ให้ตัดผ่านกราฟ สังเกตว่า ไม่มีกรณีใดเลยที่เส้นตรงลากผ่านกราฟแล้วเกิดจุดตัดกราฟมากกว่า 1 จุด ดังนั้น กราฟดังกล่าวเป็นฟังก์ชัน
2.
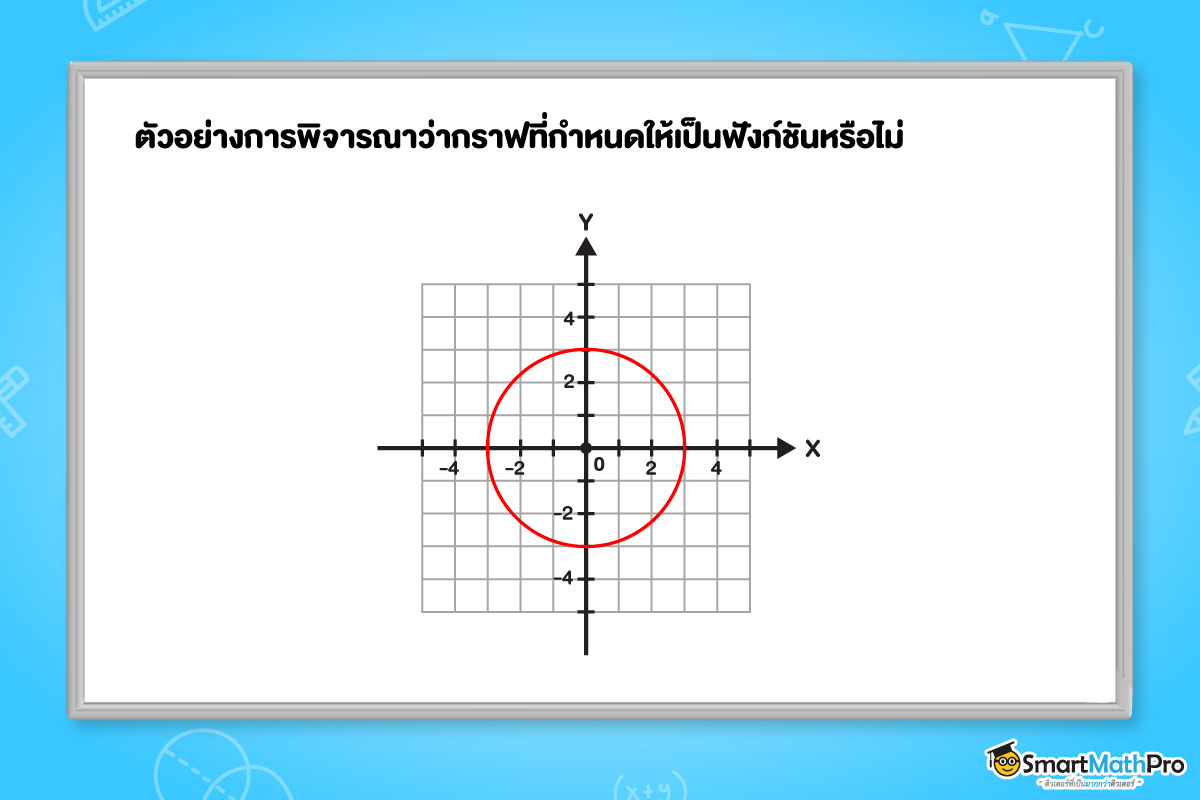
วิธีทำ
ลากเส้นตรงในแนวตั้ง (ขนานแกน Y) ให้ตัดผ่านกราฟ สังเกตว่า มีบางกรณีที่เส้นตรงลากผ่านกราฟแล้วเกิดจุดตัดกราฟมากกว่า 1 จุด เช่น
ดังนั้น กราฟดังกล่าวไม่เป็นฟังก์ชัน
ประเภทของฟังก์ชัน
ฟังก์ชันที่เราศึกษานั้นสามารถแบ่งออกได้เป็น 3 ประเภทหลัก ๆ ได้แก่
1. ฟังก์ชันจาก A ไป B
บทนิยาม
f เป็นฟังก์ชันจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนเป็น A และเรนจ์เป็นสับเซตของ B
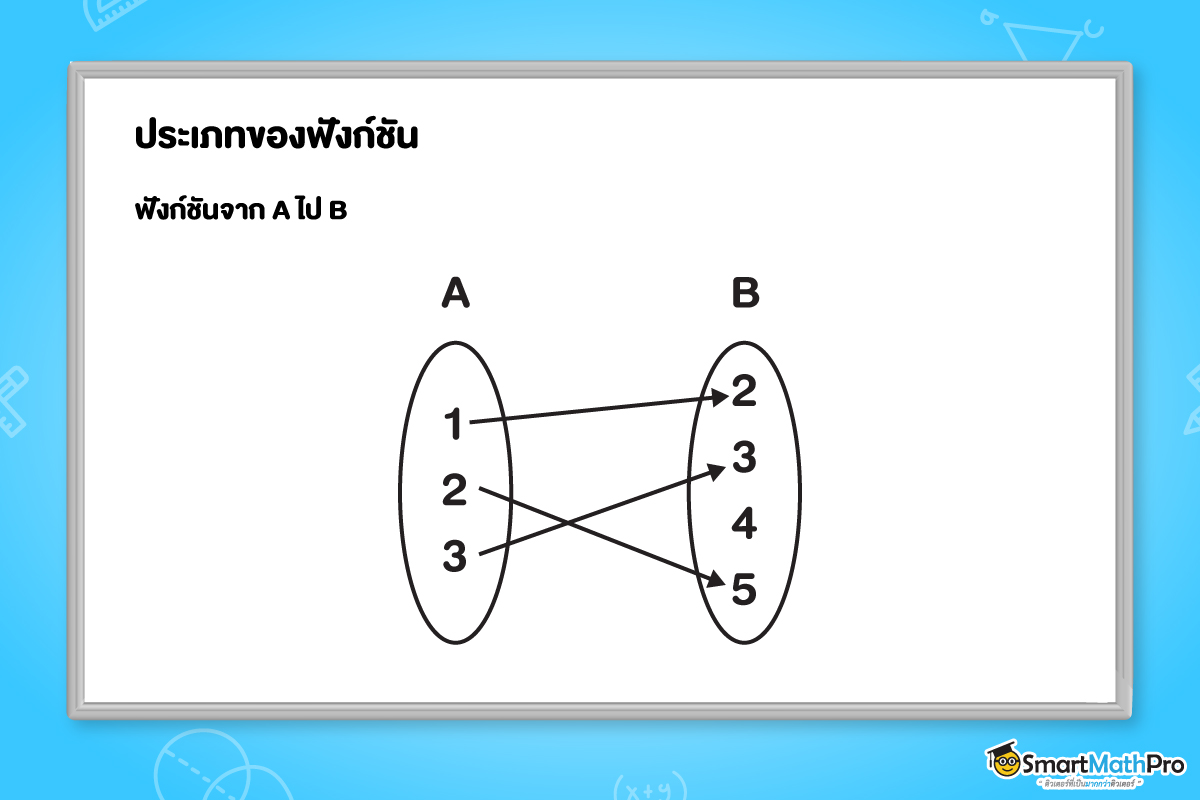
สังเกตได้ว่าฟังก์ชัน จาก A ไป B จะมีสมาชิกตัวหน้าอยู่ใน A และมีสมาชิกตัวหลังอยู่ใน B เสมอ โดยสมาชิกใน A จะถูกใช้ในฟังก์ชันหมดทุกตัว แต่สมาชิกใน B จะถูกใช้ในฟังก์ชันหมดทุกตัวหรือไม่ก็ได้
2. ฟังก์ชันจาก A ไปทั่วถึง B
บทนิยาม
f เป็นฟังก์ชันจาก A ไปทั่วถึง B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนเป็น A และเรนจ์เป็น B
เช่น
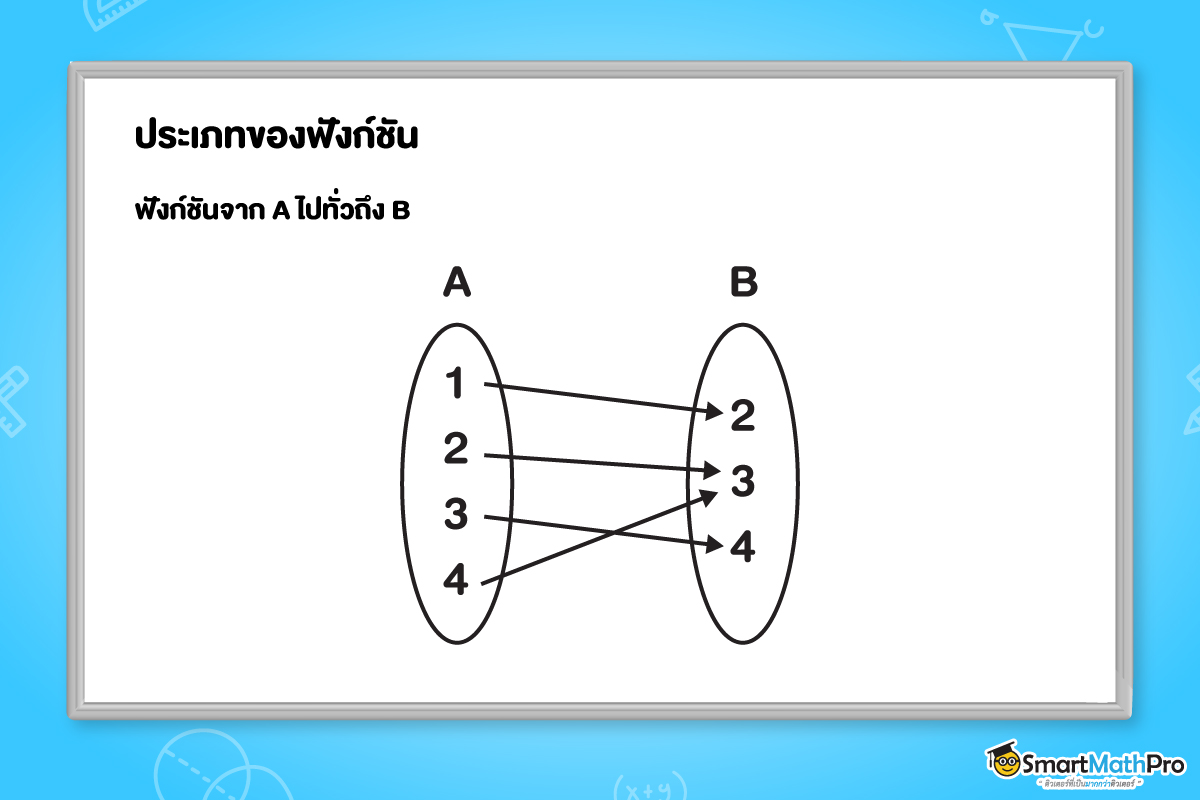
สังเกตได้ว่าฟังก์ชัน จาก A ไปทั่วถึง B สมาชิกทุกตัวใน B จะถูกใช้ในฟังก์ชันทั้งหมด
3. ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B
บทนิยาม
f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันจาก A ไป B ซึ่งสำหรับ katex is not defined และ katex is not defined ใด ๆ ใน A ถ้า katex is not defined แล้ว katex is not defined
เช่น
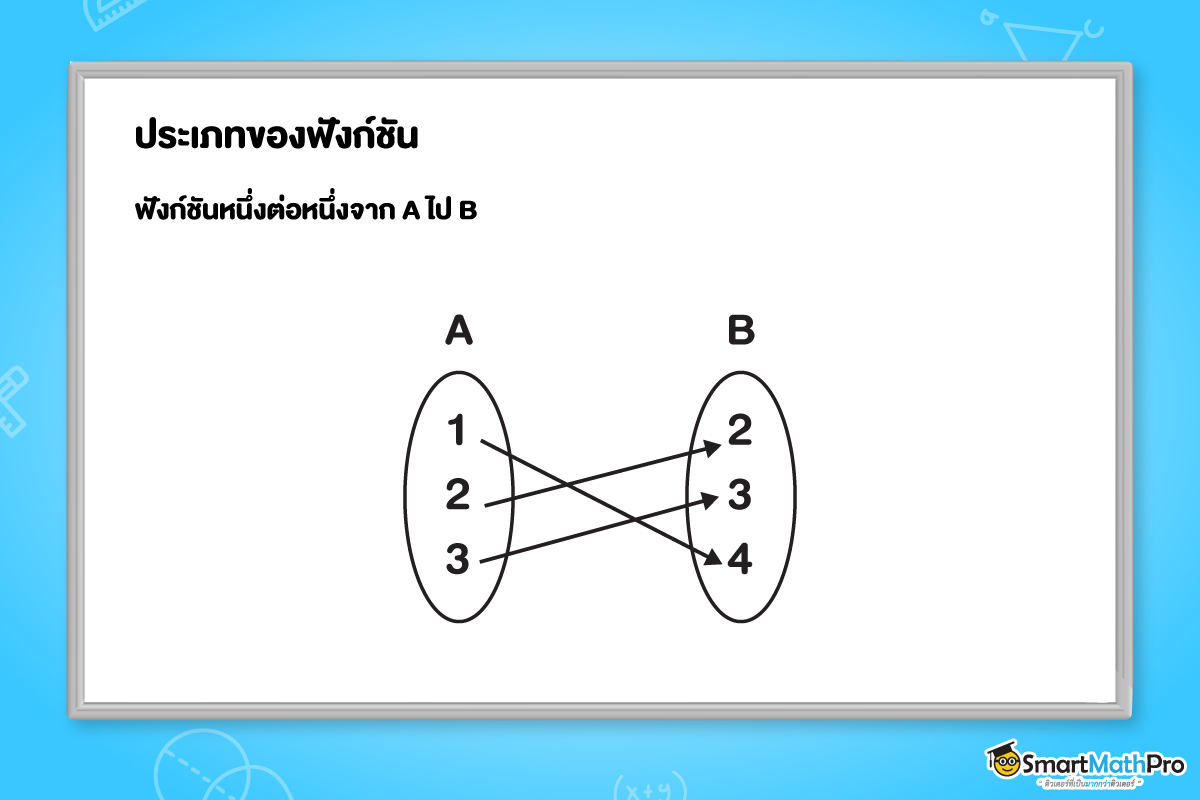
สังเกตได้ว่าฟังก์ชัน 1-1 จาก A ไป B สมาชิกใน B จะถูกใช้ในฟังก์ชันไม่เกิน 1 ตัวเสมอ
ซึ่งการตรวจสอบกราฟว่าเป็นฟังก์ชัน 1-1 มั้ย สามารถทำได้โดยลากเส้นในแนวนอน (ขนานแกน X) ให้ตัดกับกราฟ
ถ้ามีกรณีใดเกิดจุดตัดระหว่างกราฟและเส้นในแนวนอนมากกว่า 1 จุด กราฟดังกล่าวจะไม่เป็นฟังก์ชัน 1-1
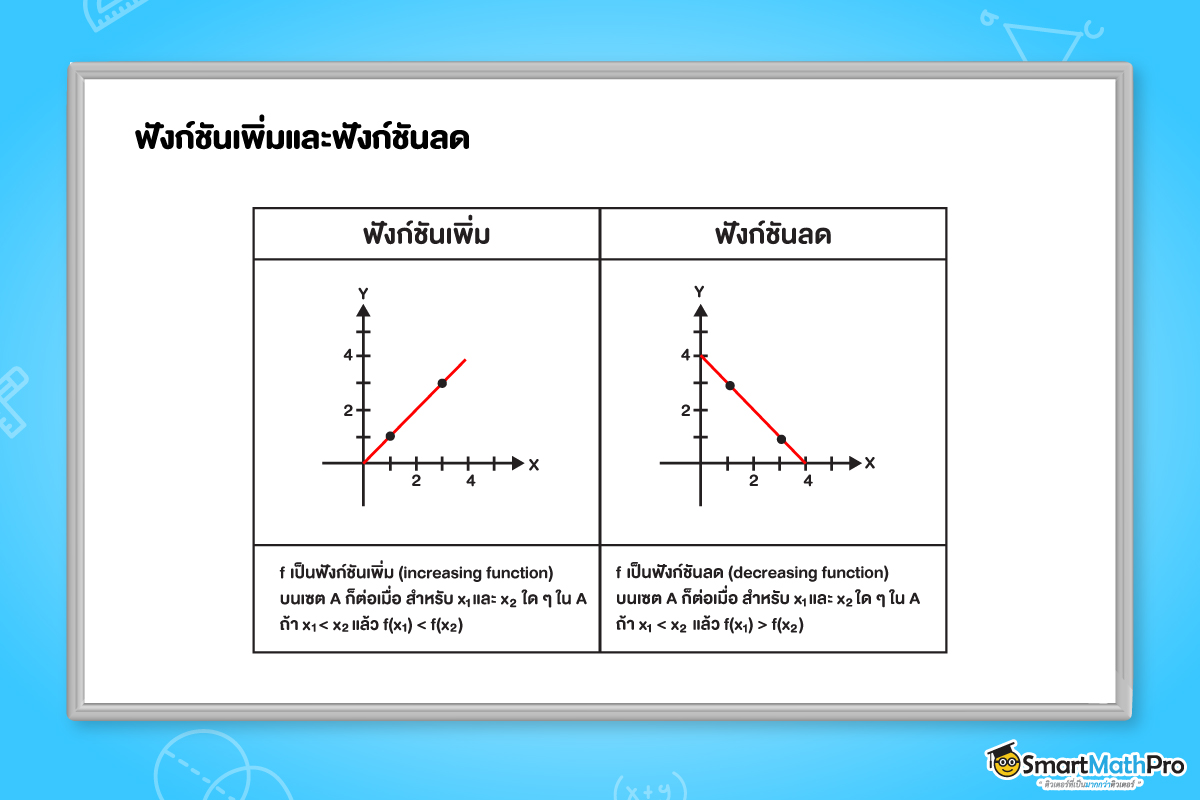
ฟังก์ชันเพิ่มและฟังก์ชันลด
บทนิยาม
ให้ f เป็นฟังก์ชันซึ่งมีโดเมนและเรนจ์เป็นสับเซตของจำนวนจริง และ A เป็นสับเซตของโดเมน
เช่น ให้ f เป็นฟังก์ชันที่มีกราฟดังรูป
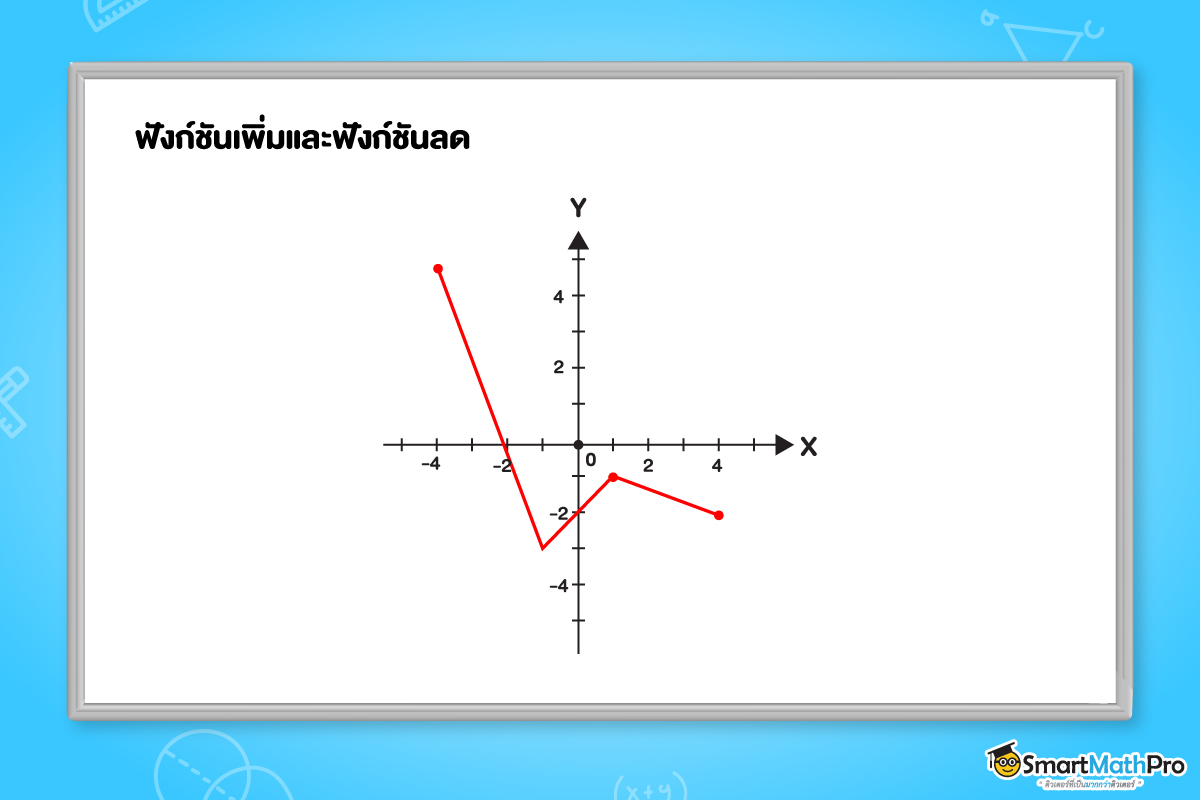
f เป็นฟังก์ชันเพิ่มบนช่วง katex is not defined และ
f เป็นฟังก์ชันลดบนช่วง katex is not defined และ katex is not defined
การดำเนินการของฟังก์ชัน
เรารู้จักฟังก์ชันกันมาพอสมควรแล้ว เดี๋ยวเราลองมาสร้างฟังก์ชันใหม่ที่ใช้ฟังก์ชันเดิมเป็นองค์ประกอบดีกว่า เนื่องจาก ฟังก์ชันที่มีโดเมนและเรนจ์เป็นเซตของจำนวนที่สามารถบวก ลบ คูณ และหารได้ ดังนั้นเราจะใช้การดำเนินการต่าง ๆ
มาสร้างฟังก์ชันใหม่ดูบ้าง
พีชคณิตของฟังก์ชัน
บทนิยาม
ให้ f และ g เป็นฟังก์ชันที่มีโดเมนและเรนจ์เป็นสับเซตของ katex is not defined
กำหนดฟังก์ชัน katex is not defined และ katex is not defined ดังนี้
katex is not defined
katex is not defined
katex is not defined
katex is not defined เมื่อ katex is not defined
ตัวอย่างที่ 5 ให้ katex is not defined และ katex is not defined จงหา katex is not defined และ katex is not defined
วิธีทำ เนื่องจากโดเมนของ f คือ katex is not defined และโดเมนของ g คือ katex is not defined ดังนั้น
katex is not defined
katex is not defined
และ
katex is not defined
katex is not defined
ฟังก์ชันประกอบ
บทนิยาม
ให้ f และ g เป็นฟังก์ชัน โดยที่ katex is not defined
ฟังก์ชันประกอบของ f และ g เขียนแทนด้วย katex is not defined คือฟังก์ชันที่โดเมน คือ
katex is not defined
และกำหนด katex is not defined โดย
katex is not defined สำหรับทุก x ใน katex is not defined
ตัวอย่างที่ 6 ให้ katex is not defined และ katex is not defined จงหา katex is not defined และ
katex is not defined
วิธีทำ จาก katex is not defined และ katex is not defined จะได้
katex is not defined
katex is not defined
katex is not defined
และ
katex is not defined
katex is not defined
katex is not defined
ฟังก์ชันผกผัน
ในเรื่องตัวผกผันของความสัมพันธ์ เราหาได้จากการสลับสมาชิกตัวหน้าและสมาชิกตัวหลังของแต่ละคู่อันดับที่เป็นสมาชิกในความสัมพันธ์นั้น ลองคิดดูดี ๆ ฟังก์ชันก็เป็นความสัมพันธ์หนึ่งเช่นกัน ดังนั้น เราจึงสามารถใช้วิธีเดียวกันในการหาได้ แต่ตัวผกผันของฟังก์ชันนั้นไม่จำเป็นต้องเป็นฟังก์ชันเสมอไป
เช่น katex is not defined เป็นฟังก์ชัน
แต่เราจะได้ katex is not defined ไม่เป็นฟังก์ชัน
บทนิยาม
ให้ f เป็นฟังก์ชัน จะได้ว่า f มีฟังก์ชันผกผัน ก็ต่อเมื่อ f เป็นฟังก์ชัน 1 – 1
ตัวอย่างที่ 7 ฟังก์ชัน f เป็นฟังก์ชัน 1 – 1 ซึ่งกำหนดโดย katex is not defined จงหาฟังก์ชันผกผัน
วิธีทำ
ให้ katex is not defined
จะได้ katex is not defined ต้องการหาตัวผกผัน
(เปลี่ยน x เป็น y และ เปลี่ยน y เป็น x)
จะได้ katex is not defined
(จัดรูปโดยเขียน y ให้อยู่ในรูปของ x)
จะได้ katex is not defined
ดังนั้น katex is not defined
ดูคลิปติวฟรี ความสัมพันธ์และฟังก์ชัน ม.4
ดูคลิปติวฟรีอื่น ๆ ได้ที่ YouTube : SmartMathPro
เป็นยังไงบ้างกับสรุปบทความสัมพันธ์และฟังก์ชัน ม.4 อาจจะเนื้อหาเยอะหน่อย แต่ถ้าน้อง ๆ ทบทวนเนื้อหา รวมถึง
ฝึกทำโจทย์บ่อย ๆ พี่เชื่อว่่าทุกคนจะเก่งขึ้น และทำคะแนนสอบได้ดีแน่นอนน ซึ่งถ้าใครอยากได้โจทย์ไปฝึกซ้อมมือเพิ่มเติม เสริมความมั่นใจ พี่ก็มีโจทย์และแบบฝึกหัดในคลังข้อสอบให้ทุกคนได้ไปดาวน์โหลดมาฝึกทำกันแบบฟรี ๆ ด้วยน้าา แวะเข้าไปดูกันได้เลยย
แต่ถ้าน้อง ๆ คนไหนที่ทบทวนเนื้อหา รวมถึงฝึกทำโจทย์เองแล้วก็ยังไม่เข้าใจ อยากได้คนช่วยไกด์ พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35%
โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
จำนวนจริง ม.4 สรุปครบม้วนเดียวจบ พร้อมแจกโจทย์จำนวนจริงและวิธีทำ
เซต (Set) คืออะไร สรุปเนื้อหาเซต ม.4 พร้อมโจทย์และเฉลย
ตรรกศาสตร์ ม.4 สรุปครบทุกเนื้อหาพร้อมโจทย์ตรรกศาสตร์และวิธีทำ - SmartMathPro
คณิตศาสตร์ ม.4 เทอม 1,2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม
คณิตศาสตร์ ม.5 เทอม 1 เทอม 2 เรียนอะไร? สรุปครบทั้งพื้นฐานและเพิ่มเติม
คณิตศาสตร์ ม.6 เทอม 1 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง?
คณิตศาสตร์ ม.ปลาย (ม.4 ม.5 ม.6) หลักสูตรใหม่ เรียนเรื่องอะไรบ้าง ?
บทความ แนะนำ
คณิตศาสตร์ ม.4 เทอม 1, ม.4 เทอม 2 คณิตพื้นฐานและเพิ่มเติม เรียนอะไรบ้าง ?
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
