พอพูดชื่อ “วงกลม” พี่ว่าคงไม่มีใครที่ไม่รู้จักชื่อนี้แน่นอน และถ้าเราพูดถึงวงกลมในวิชาคณิตศาสตร์ น้อง ๆ หลายคนอาจจะคุ้นหูกันมาบ้าง เพราะเคยเรียนผ่านมาแล้วตอนชั้นประถม แต่เราจะได้กลับมาเจอเรื่องนี้กันอีกครั้งในเนื้อหา วงกลม ม.3 ด้วยน้าา
ใครที่กำลังสงสัยว่าเนื้อหาจะเป็นยังไง พี่ก็ได้สรุปมาให้ทุกคนหมดแล้วในบทความนี้ ตั้งแต่ส่วนประกอบของวงกลม ไปจนถึงทฤษฎีบทต่าง ๆ (แถมท้ายบทความยังมีแบบฝึกหัดแจกฟรีด้วย !!) รับรองว่าเนื้อหาสนุกกว่าเดิมแน่นอนน ถ้าพร้อมแล้ว ไปลุยกันเลยย > <
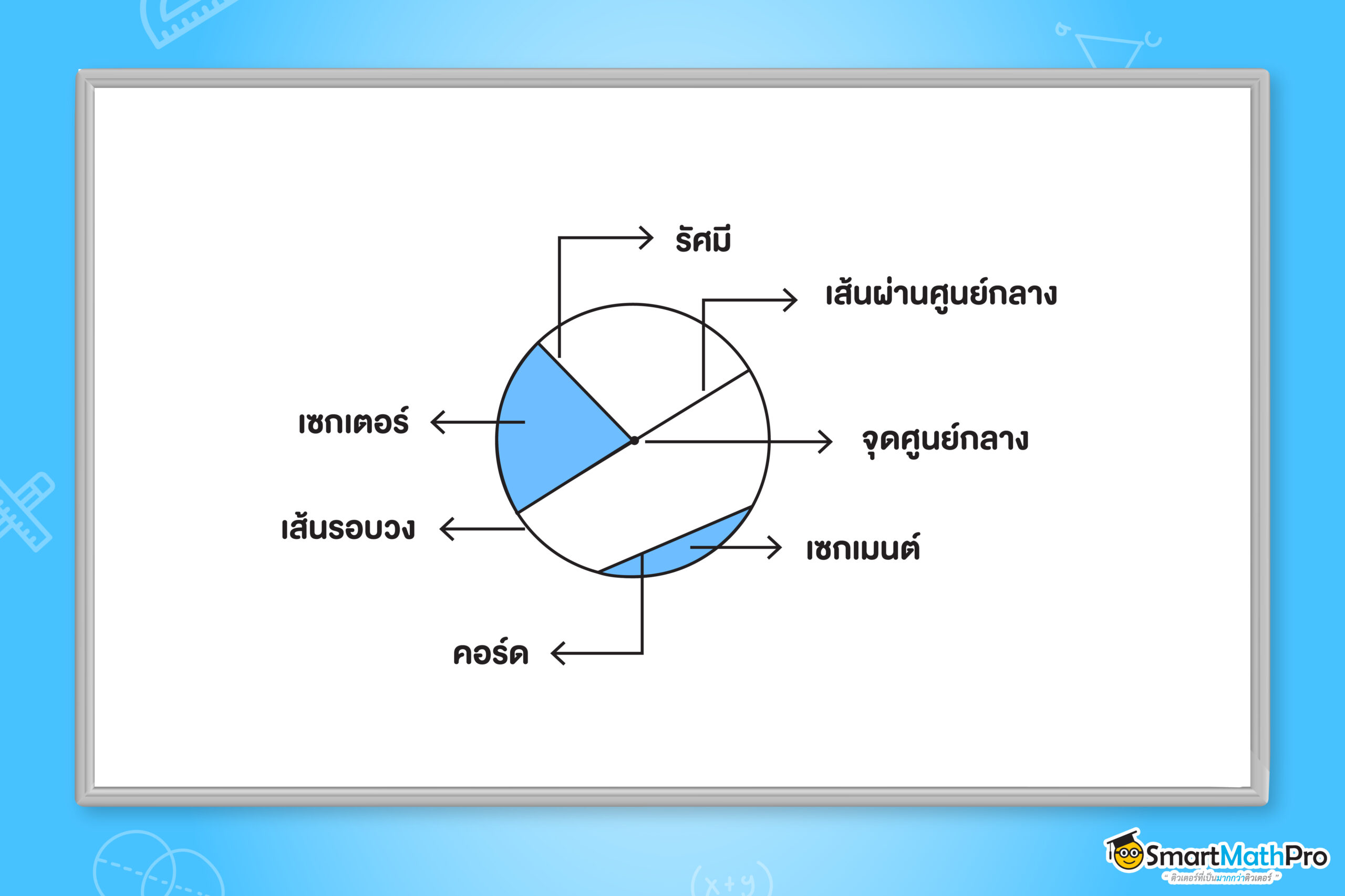
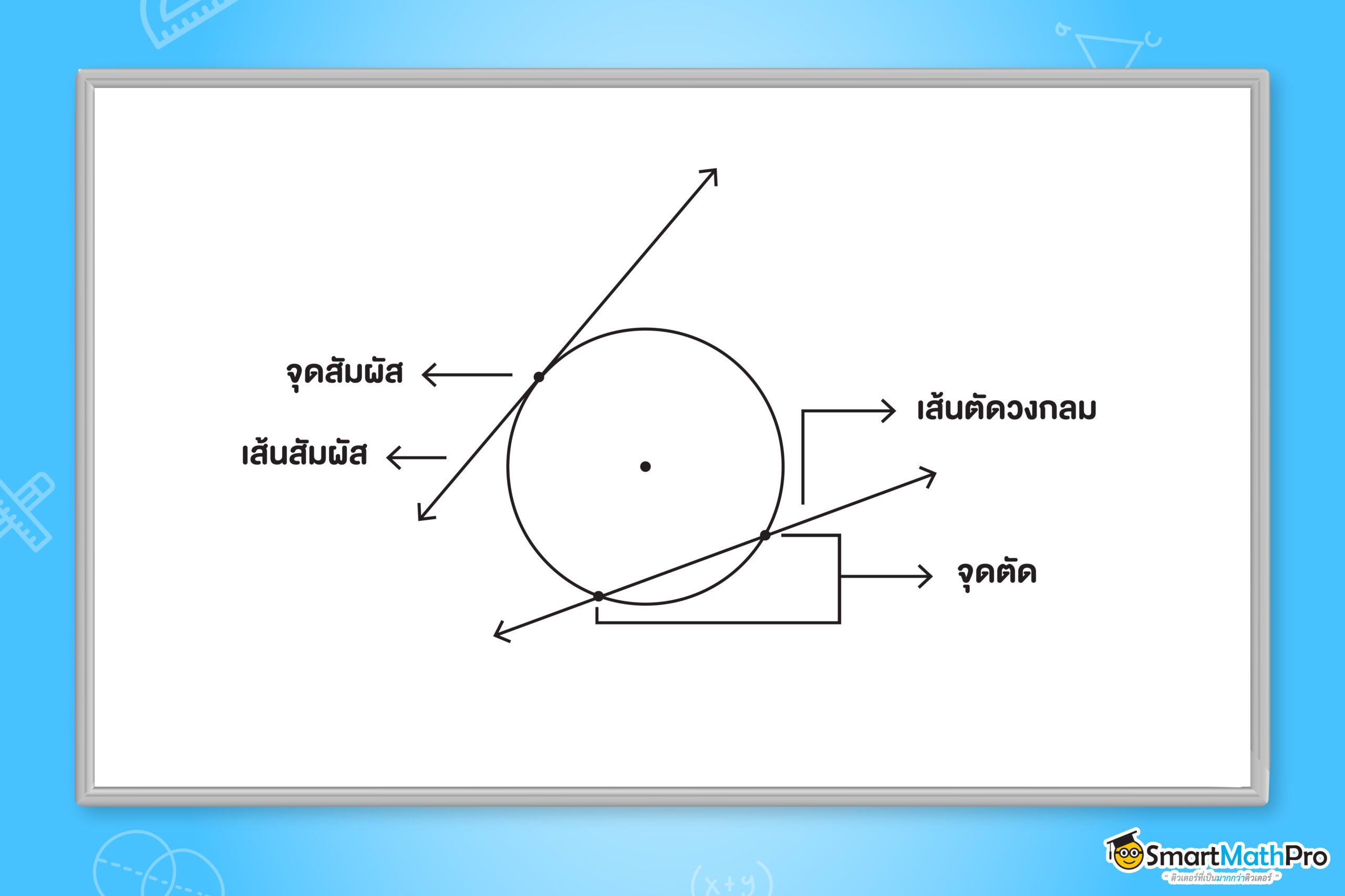
จากรูปด้านบนนี้ จะเห็นว่ามีส่วนประกอบหลัก ๆ อยู่ 11 องค์ประกอบ คือ
- จุดศูนย์กลาง คือ จุดที่จุดทุกจุดบนวงกลมที่อยู่ห่างจากจุดตรึงนี้เป็นระยะเท่ากัน
- เส้นผ่านศูนย์กลาง คือ ส่วนของเส้นตรงที่ผ่านจุดศูนย์กลาง และมีจุดปลายทั้งสองอยู่บนเส้นรอบวง
- รัศมี คือ ส่วนของเส้นตรงที่ลากจากจุดศูนย์กลางกับ จุดใด ๆ บนเส้นรอบวง
- เส้นรอบวง คือ เส้นโค้งที่ปิดบนระนาบที่แสดงเป็นวงกลม
- คอร์ด คือ ส่วนของเส้นตรงที่ลากจากเส้นรอบวงฝั่งหนึ่ง ไปยังเส้นรอบวงอีกฝั่งหนึ่ง
- เซกเมนต์ คือ พื้นที่ที่ล้อมถูกรอบด้วยส่วนของเส้นรอบวงและคอร์ด
- เซกเตอร์ คือ พื้นที่ที่ล้อมถูกรอบด้วยส่วนของเส้นรอบวงและรัศมี 2 เส้น
- เส้นตัดวงกลม คือ เส้นตรงที่ตัดวงกลมสองจุด
- จุดตัดวงกลม คือ จุดที่เกิดจากการตัดกันระหว่างวงกลมและเส้นตัดวงกลม
- เส้นสัมผัสวงกลม คือ เส้นตรงที่ตัดวงกลมหนึ่งจุด
- จุดสัมผัสวงกลม คือ จุดที่เกิดจากการตัดกันระหว่างวงกลมและเส้นสัมผัสวงกลมเพียงหนึ่งจุด
ทฤษฎีบทวงกลม
หลังจากเรารู้จักส่วนต่าง ๆ ของวงกลมกันมาแล้ว เรามาดูกันเลยว่าในบทนี้มีทฤษฎีบทที่สำคัญ ๆ อะไรบ้าง
โดยพี่จะแบ่งทฤษฎีบทออกเป็น 3 กลุ่มใหญ่ ๆ เป็นทฤษฎีบทที่เกี่ยวกับ
1. มุมที่จุดศูนย์กลางและมุมในส่วนโค้งของวงกลม
2. คอร์ดของวงกลม
3. เส้นสัมผัสของวงกลม
แต่ละทฤษฎีบทจะมีรายละเอียดยังไงกันบ้าง ไปอ่านต่อกันได้เลย
มุมที่จุดศูนย์กลางและมุมในส่วนโค้งของวงกลม
ทฤษฎีบทวงกลมที่ 1
ในวงกลมเดียวกัน มุมที่จุดศูนย์กลางจะมีขนาดเป็นสองเท่าของขนาดของมุมในส่วนโค้งของวงกลมที่รองรับด้วยส่วนโค้งเดียวกัน
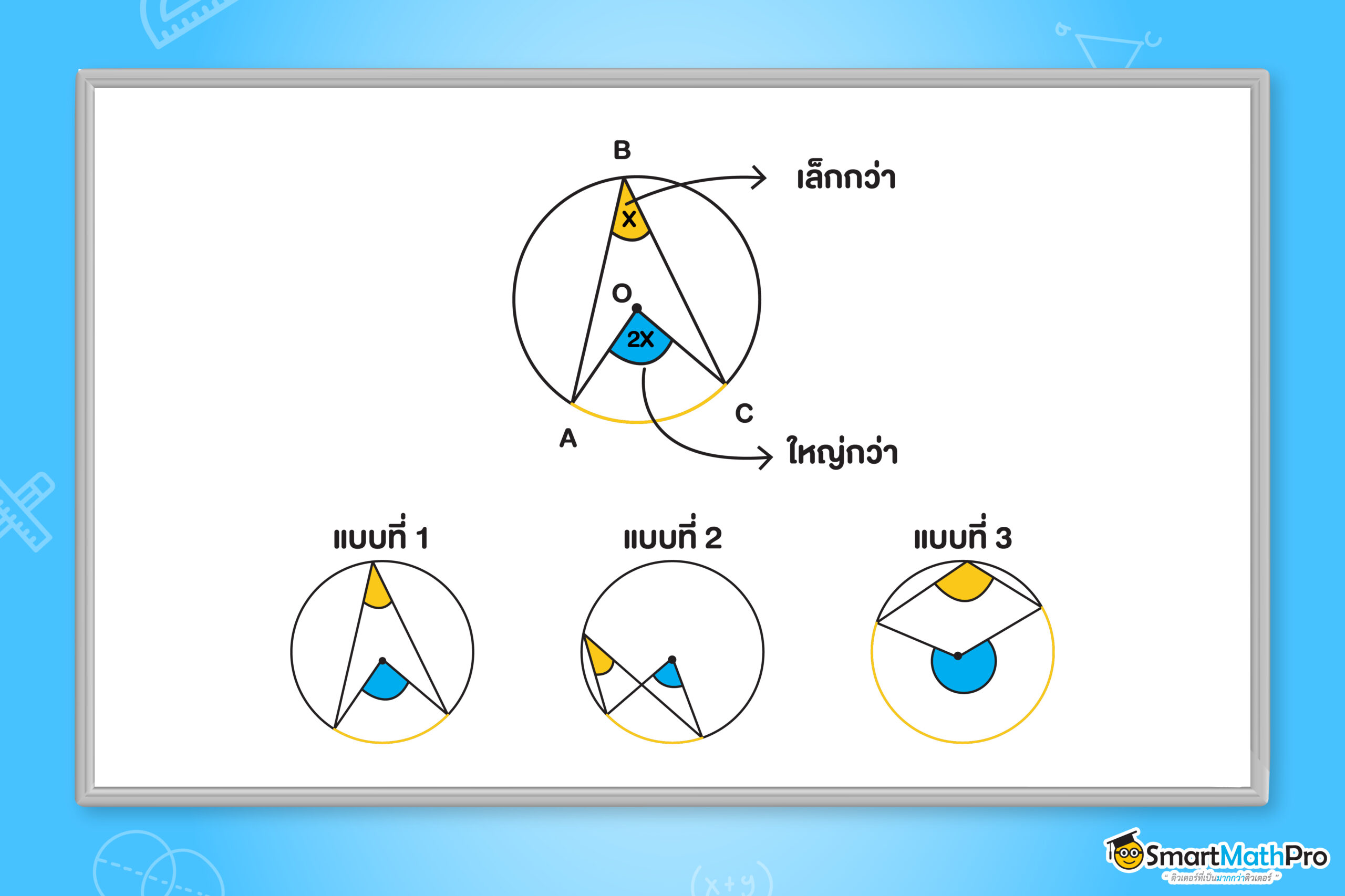
จากรูป จะเห็นว่า A\widehat{O}C ซึ่งเป็นมุมที่จุดศูนย์กลาง และ A\widehat{B}C ซึ่งเป็นมุมในส่วนโค้ง ที่ถูกรองรับด้วยส่วนโค้งเดียวกัน คือส่วนโค้ง AC แล้ว A\widehat{O}C (มุมที่จุดศูนย์กลาง) จะใหญ่เป็นสองเท่าของ A\widehat{B}C (มุมในส่วนโค้ง)
ข้อควรระวัง
อย่าจำสลับกันน้า มุมในส่วนโค้งต้องเป็นมุมที่มีขนาดเล็กกว่าเสมอ (สังเกตได้จากรูปข้างต้น) ถ้า A\widehat{O}C=60^{\circ}
แล้ว A\widehat{B}C=30^{\circ}
ซึ่งทฤษฎีบทนี้ สามารถใช้ได้ 3 แบบ ดังรูป จะเห็นว่าทั้งสามแบบมีหน้าตาที่ไม่เหมือนกัน โดยเฉพาะแบบที่ 2 และแบบที่ 3 มองเร็ว ๆ บางคนอาจจะคิดว่านี่คือคนละทฤษฎีบทกันหรือเปล่านะ รูปไม่เห็นจะเหมือนกันเลย แต่ถ้าเราสังเกตจากส่วนโค้งที่รองรับมุม แล้วมันเหมือนกับแบบที่ 1 เลย
ข้อควรระวัง
น้อง ๆ ต้องสังเกตดี ๆ น้า ว่ามุมที่จุดศูนย์กลางและมุมในส่วนโค้งถูกรองรับด้วยส่วนโค้งใด และจะต้องเป็นส่วนโค้งเดียวกันหรือยาวเท่ากันเท่านั้นนะ ถึงจะใช้ทฤษฎีบทที่ 1 นี้ได้
ทฤษฎีบทวงกลมที่ 2
ในวงกลมที่เท่ากันทุกประการหรือในวงกลมวงเดียวกัน ถ้ามุมในส่วนโค้งของวงกลมมีขนาดเท่ากัน
แล้วส่วนโค้งที่รองรับมุมเหล่านั้นจะยาวเท่ากัน
ซึ่งทฤษฎีบทนี้ จะเป็นจริงทั้งขาไปและขากลับ ซึ่งขากลับคือ ในวงกลมที่เท่ากันทุกประการหรือในวงกลมวงเดียวกัน
ถ้าส่วนโค้งที่รองรับมุมยาวเท่ากัน แล้วมุมในส่วนโค้งที่รองรับด้วยส่วนโค้งเหล่านั้นจะมีขนาดเท่ากัน หรือสามารถกล่าวได้ว่า มุมในส่วนโค้งของวงกลมมีขนาดเท่ากัน ก็ต่อเมื่อส่วนโค้งที่รองรับมุมยาวเท่ากัน นั่นเอง
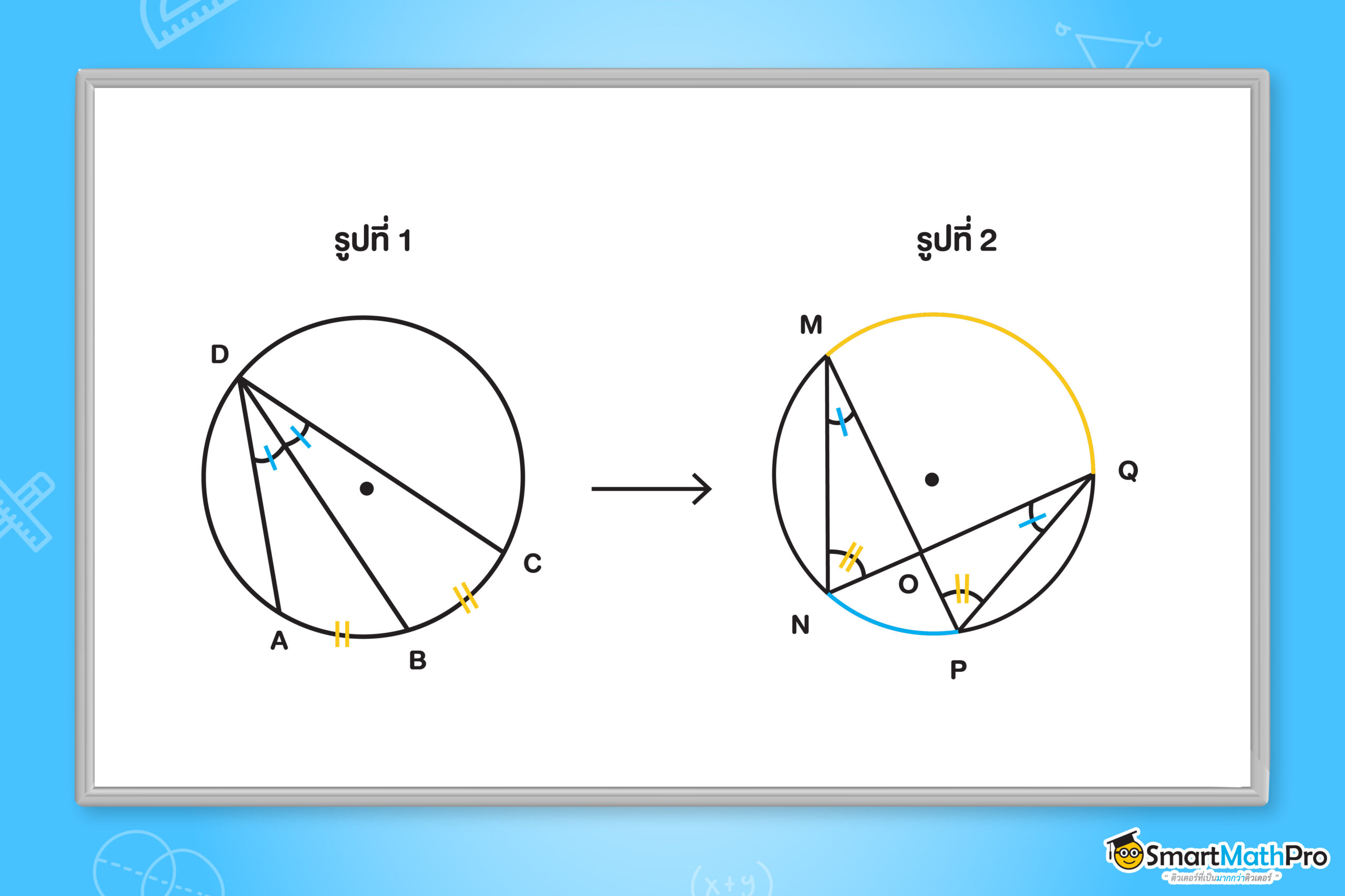
รูปที่ 1 และ 2 ข้างต้นนี้ ถ้ามองเร็ว ๆ อาจจะคิดว่ามันคือคนละทฤษฎีบทกันและไม่เกี่ยวกันโดยสิ้นเชิง แต่ในความจริงแล้วไม่เป็นแบบนั้นน้า
ถ้าลองเริ่มสังเกตจากรูปที่ 1 จะเห็นว่า A\widehat{D}B และ B\widehat{D}C มีขนาดเท่ากัน แล้วจะได้ว่าส่วนโค้ง AB ยาวเท่ากับ
ส่วนโค้ง BC (นั่นก็คือ ขาไป) หรือจะมองในทางกลับกันก็ได้นะ คือ ถ้าส่วนโค้งที่รองรับมุมยาวเท่ากัน มุมในส่วนโค้งนั้น
ก็จะมีขนาดเท่ากันไปด้วย (นั่นก็คือ ขากลับ)
แล้วถ้าเราลองพิจารณาในทำนองเดียวกัน รูปที่ 2 มุมที่รองรับด้วยส่วนโค้ง NP คือ N\widehat{M}P และ N\widehat{Q}P
แล้วทั้งสองมุมจะมีขนาดเท่ากัน (ขากลับ) หรือ มุมที่รองรับด้วยส่วนโค้ง MQ คือ M\widehat{N}Q และ M\widehat{P}Q แล้วทั้งสองมุม
จะมีขนาดเท่ากันเช่นเดียวกัน (ขาไป)
เราจะใช้ทฤษฎีบทนี้เมื่อเจอส่วนโค้งที่ยาวเท่ากัน แล้วสามารถบอกได้ว่ามุมที่เกิดจากส่วนโค้งนั้นมีขนาดเท่ากัน หรือเมื่อเจอมุมที่เกิดจากส่วนโค้งเดียวกัน แล้วมุมที่เกิดขึ้นนั้นก็จะมีขนาดเท่ากันด้วย
ข้อสังเกต
ส่วนโค้ง MQ มีความยาวมากกว่าส่วนโค้ง NP แล้วมุมที่เกิดจากส่วนโค้ง MQ มีขนาดมากกว่ามุมที่เกิดจากส่วนโค้ง NP ด้วยน้า
ทฤษฎีบทวงกลมที่ 3
มุมในครึ่งวงกลมมีขนาด 90 องศา หรือหนึ่งมุมฉาก
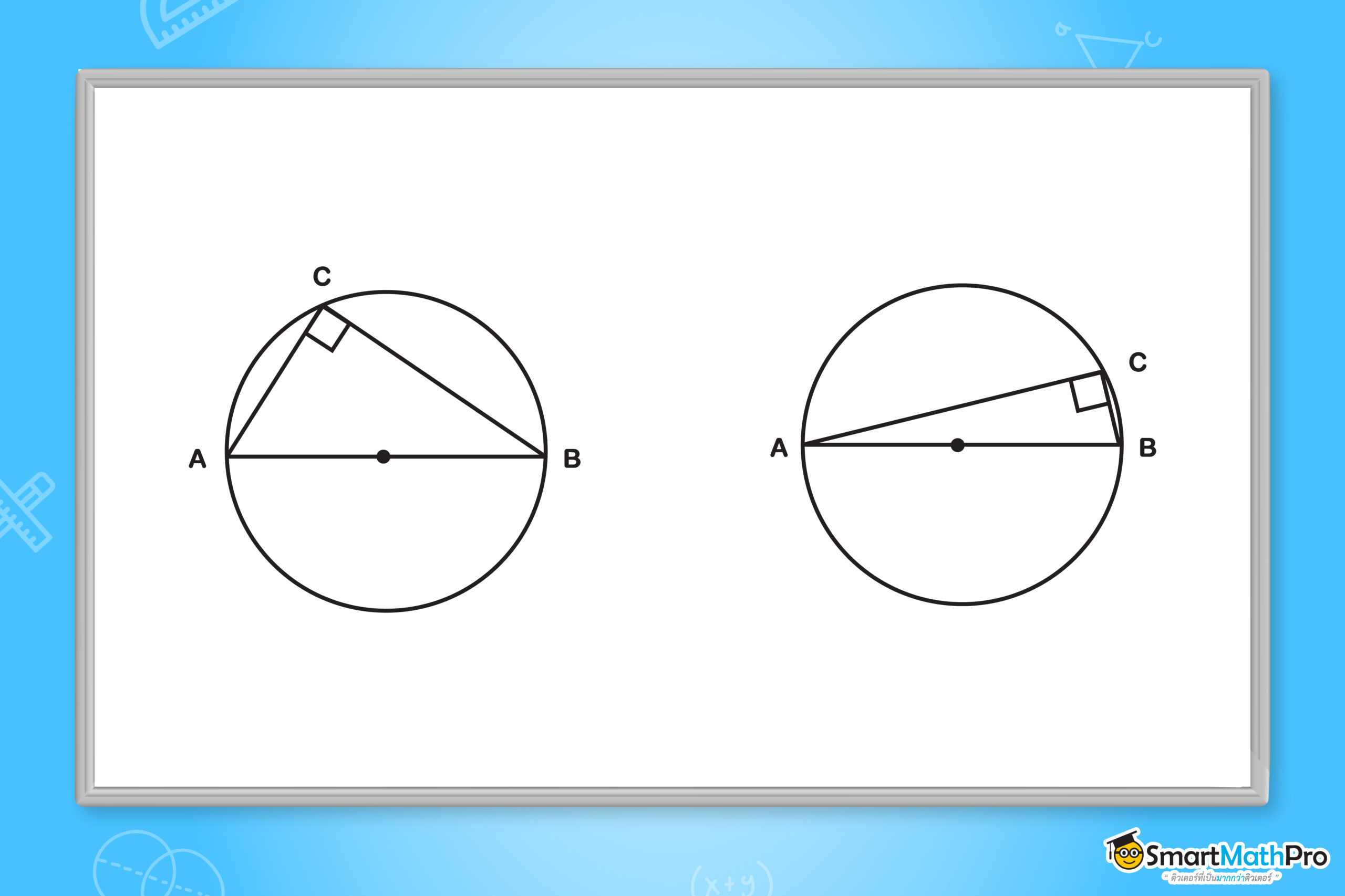
จากรูป \overline{AB} เป็นเส้นผ่านศูนย์กลางของวงกลม โดยมี C เป็นจุดบนส่วนโค้งของวงกลม และ A\widehat{C}B เป็นมุมในส่วนโค้งของวงกลม จะมีขนาดเท่ากับ 90^{\circ}
ถ้ารูปสามเหลี่ยม ABC ที่แนบอยู่ด้านในของวงกลมมี \overline{AB} เป็นเส้นผ่านศูนย์กลางของวงกลม ไม่ว่าเราจะเลื่อนจุด C
ไปบนส่วนโค้งของวงกลมที่ใดก็ตามที่ไม่ทับกับจุด A และ จุด B รูปสามเหลี่ยมที่ได้จะแบนหรือใหญ่แค่ไหน มุม C ก็จะเป็นมุมฉากเสมอ
ทฤษฎีบทวงกลมที่ 4
ถ้ารูปสี่เหลี่ยมใด ๆ เป็นรูปสี่เหลี่ยมแนบในวงกลม แล้วผลบวกของขนาดของมุมตรงข้ามจะเท่ากับ 180 องศาหรือ
สองมุมฉาก
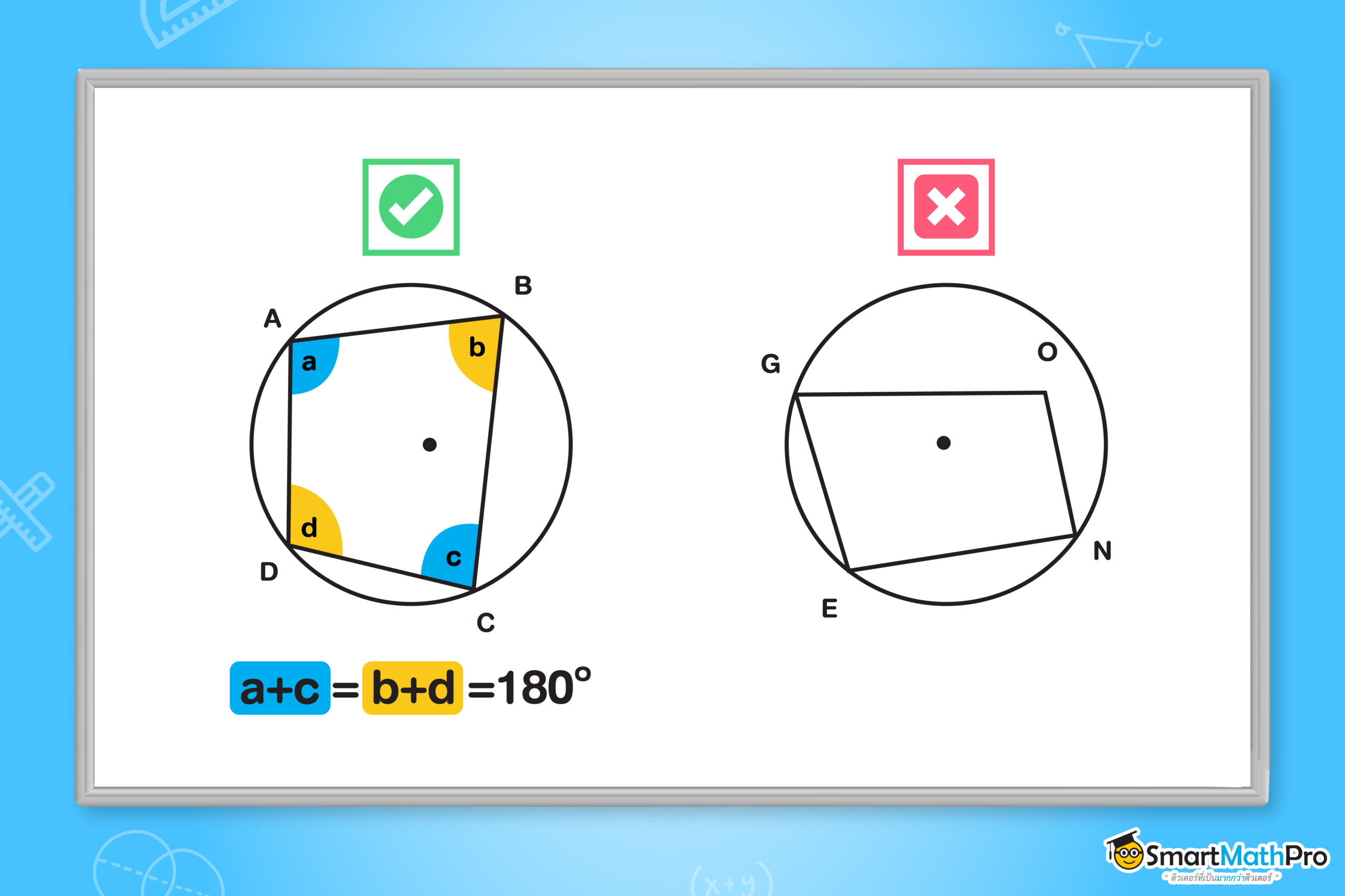
จากรูปด้านซ้าย จะเห็นว่าจุด A, B, C, และ D เป็นจุดบนส่วนโค้งของวงกลม จะเห็นว่ารูปสี่เหลี่ยม ABCD เป็นรูปสี่เหลี่ยมที่แนบอยู่ด้านในของวงกลม ซึ่งมีมุมภายในของรูปสี่เหลี่ยมเป็น a, b, c, d
ถ้ามุม A อยู่ตรงข้ามกับมุม C แล้วผลบวกของ A กับ C จะเท่ากับ 180 องศา ในทำนองเดียวกัน ถ้ามุม B อยู่ตรงข้าม
กับมุม D แล้วผลบวกของ B กับ D จะเท่ากับ 180 องศา
ข้อควรระวัง
จากรูปด้านขวาข้างต้น จุด O ไม่ได้อยู่บนส่วนโค้งของวงกลม
ดังนั้น รูปสี่เหลี่ยม GONE ไม่เรียกว่าเป็นรูปสี่เหลี่ยมที่แนบอยู่ในวงกลมน้า
ตัวอย่างที่ 1
จากรูป กำหนดให้ \overline{AD} และ \overline{BC} เป็นเส้นผ่านศูนย์กลางของวงกลม O และ C\widehat{E}D= 120^{\circ} จงหาขนาดของ A\widehat{B}C
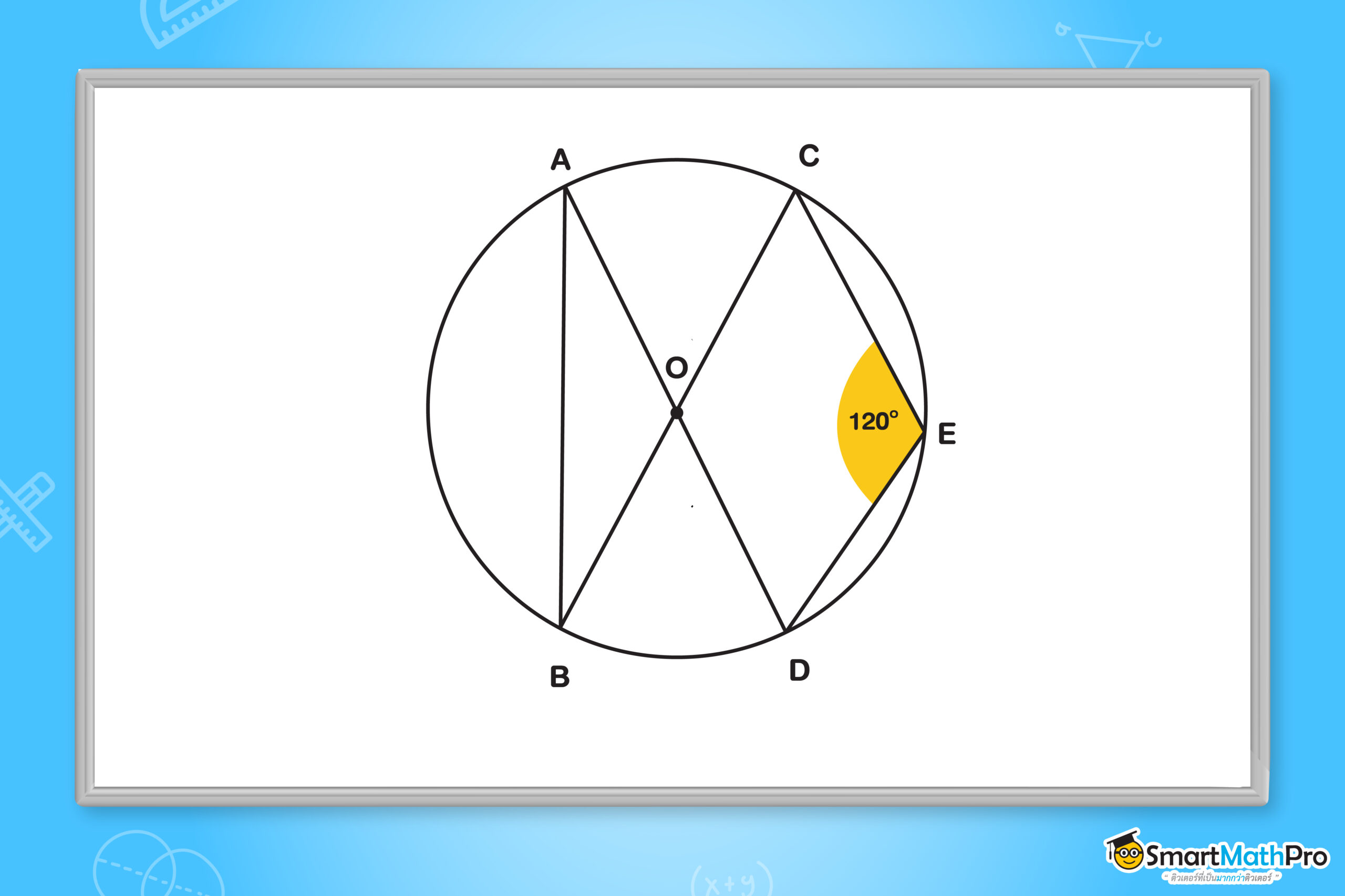
วิธีทำ
จาก ทฤษฎีบทที่ 1 ในวงกลมเดียวกัน มุมที่จุดศูนย์กลางจะมีขนาดเป็นสองเท่าของขนาดของมุมในส่วนโค้งของวงกลมที่รองรับด้วยส่วนโค้งเดียวกันและ C\widehat{E}D= 120^{\circ}
จะได้ว่า มุมกลับ COD= 240^{\circ}
จาก วงกลมมีขนาดมุมที่จุดศูนย์กลางรวมกันเป็น 360^{\circ}
ดังนั้น C\widehat{O}D= 360-240=120^{\circ}
จาก A\widehat{O}B และ C\widehat{O}D มุมตรงข้ามจะมีขนาดเท่ากัน
จะได้ว่า A\widehat{O}B=C\widehat{O}D
และ \overline{AO}, \overline{BO} เป็นรัศมีของวงกลมเดียวกัน
จะได้ว่า \overline{AO}=\overline{BO}
ดังนั้น \Delta AOB เป็นรูปสามเหลี่ยมหน้าจั่ว
จาก ขนาดของมุมภายในทั้งสามมุมของรูปสามเหลี่ยมรวมกันได้ 180^{\circ} และมุมที่ฐานของรูปสามเหลี่ยมหน้าจั่วทั้งสองมุม
มีขนาดเท่ากัน
จะได้ว่า A\widehat{B}C= \frac{180-120}{2}=30^{\circ}
ตอบ 30^{\circ}
คอร์ดของวงกลม
ทฤษฎีบทวงกลมที่ 5
ส่วนของเส้นตรงซึ่งผ่านจุดศูนย์กลางของวงกลม และตัดกับคอร์ดที่ไม่ใช่เส้นผ่านศูนย์กลางจะมีสมบัติดังนี้
- ถ้าส่วนของเส้นตรงแบ่งครึ่งคอร์ด แล้วส่วนของเส้นตรงนั้นจะตั้งฉากกับคอร์ด
- ถ้าส่วนของเส้นตรงตั้งฉากกับคอร์ด แล้วส่วนของเส้นตรงนั้นจะแบ่งครึ่งคอร์ด
จากทฤษฎีบทที่ 5 จะเห็นว่า ข้อที่ 1. และข้อที่ 2. เปรียบเสมือนขาไปและขากลับซึ่งกันและกัน แสดงว่าประโยคนี้เป็นจริง
ทั้งขาไปและขากลับ นั่นเอง หรือสามารถกล่าวเพิ่มได้อีกว่า เส้นตรงที่ตั้งฉากและแบ่งครึ่งคอร์ดของวงกลมจะผ่านจุดศูนย์กลางของวงกลมนั้น
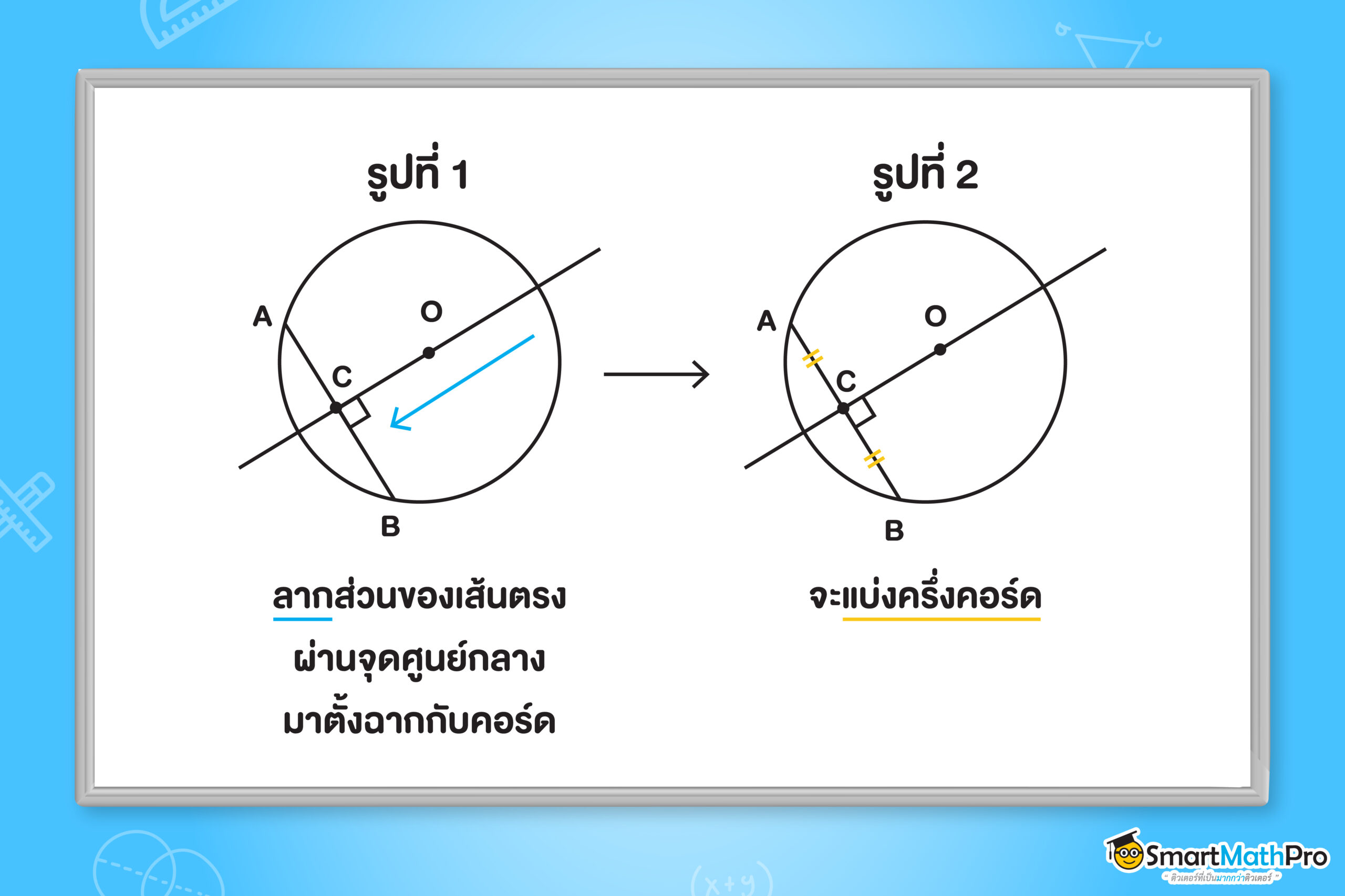
จากรูปที่ 1 เมื่อลากเส้นตรงผ่านจุด O มาตั้งฉาก \overline{AB} ซึ่งเป็นคอร์ดของวงกลม O ที่จุด C จะทำให้ความยาวของ \overline{AC} และ \overline{BC} ยาวเท่ากัน (เป็นดังรูปที่ 2)
ทฤษฎีบทวงกลมที่ 6
ในวงกลมเดียวกัน ถ้าคอร์ดสองเส้นยาวเท่ากัน แล้วคอร์ดทั้งสองนั้นจะอยู่ห่างจากจุดศูนย์กลางเป็นระยะเท่ากัน
ซึ่งทฤษฎีบทนี้ จะเป็นจริงทั้งขาไปและขากลับ ซึ่งขากลับ คือ ในวงกลมเดียวกัน ถ้าคอร์ดสองเส้นอยู่ห่างจากจุดศูนย์กลางเป็นระยะเท่ากัน แล้วคอร์ดทั้งสองนั้นจะยาวเท่ากัน
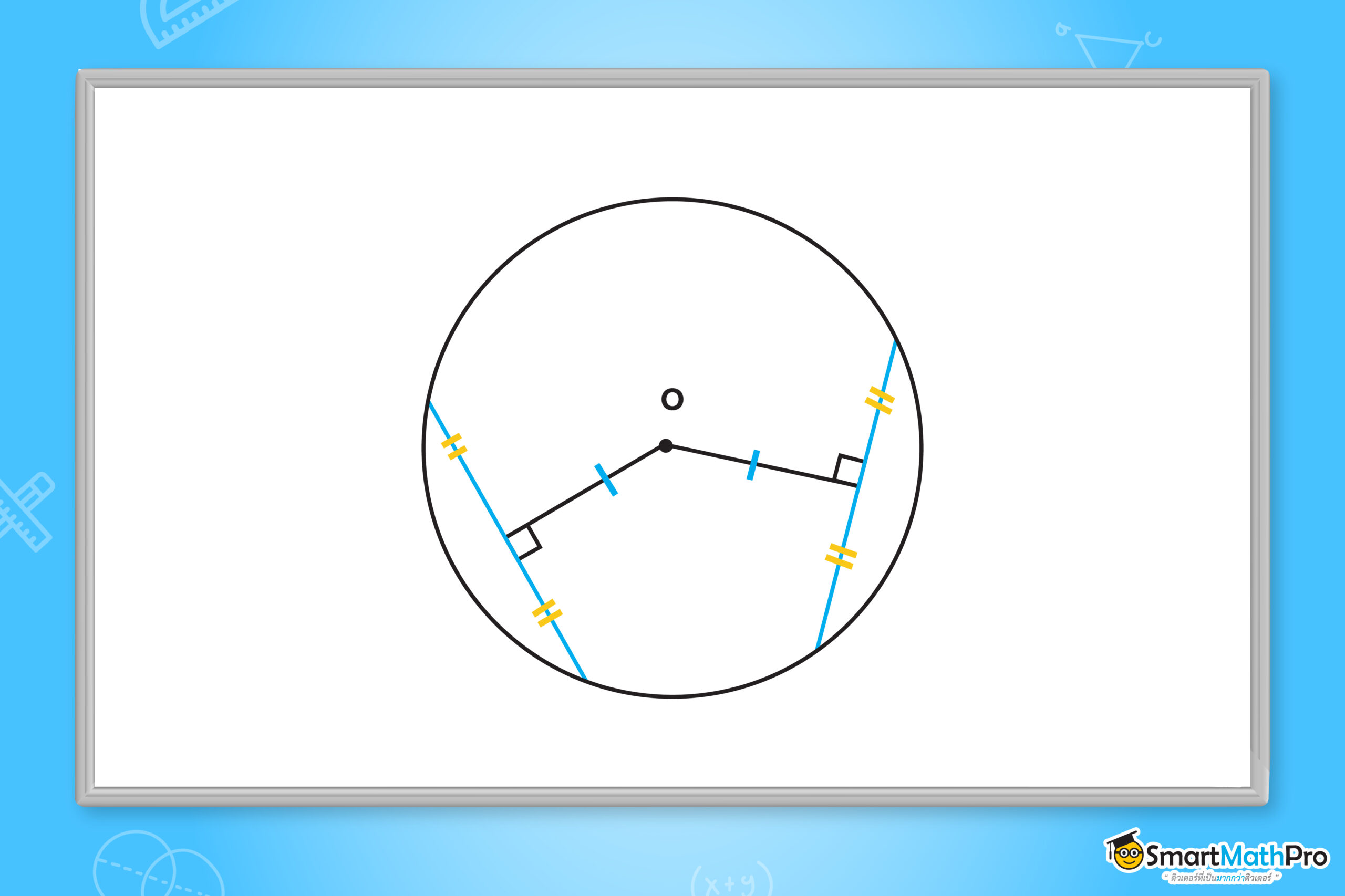
จากรูป น้อง ๆ อาจเริ่มสังเกตจากความยาวของคอร์ดทั้งสองเส้นในวงกลมมีความยาวเท่ากัน เลยทำให้ระยะห่างระหว่างจุด O (จุดศูนย์กลาง) กับคอร์ดเส้นทางซ้าย และ ระยะห่างระหว่างจุด O (จุดศูนย์กลาง) กับคอร์ดเส้นทางขวาห่างเท่ากัน
ในทางกลับกัน ถ้าเริ่มสังเกตจากระยะห่างระหว่างจุด O (จุดศูนย์กลาง) กับคอร์ดเส้นทางซ้าย และ ระยะห่างระหว่างจุด O (จุดศูนย์กลาง) กับคอร์ดเส้นทางขวาห่างเท่ากัน เลยทำให้ ความยาวของความยาวของคอร์ดทั้งสองเส้นในวงกลมนี้ยาวเท่ากันนั่นเอง
ตัวอย่างที่ 2
จากวงกลม O ที่กำหนดให้ จงหาค่าของ x
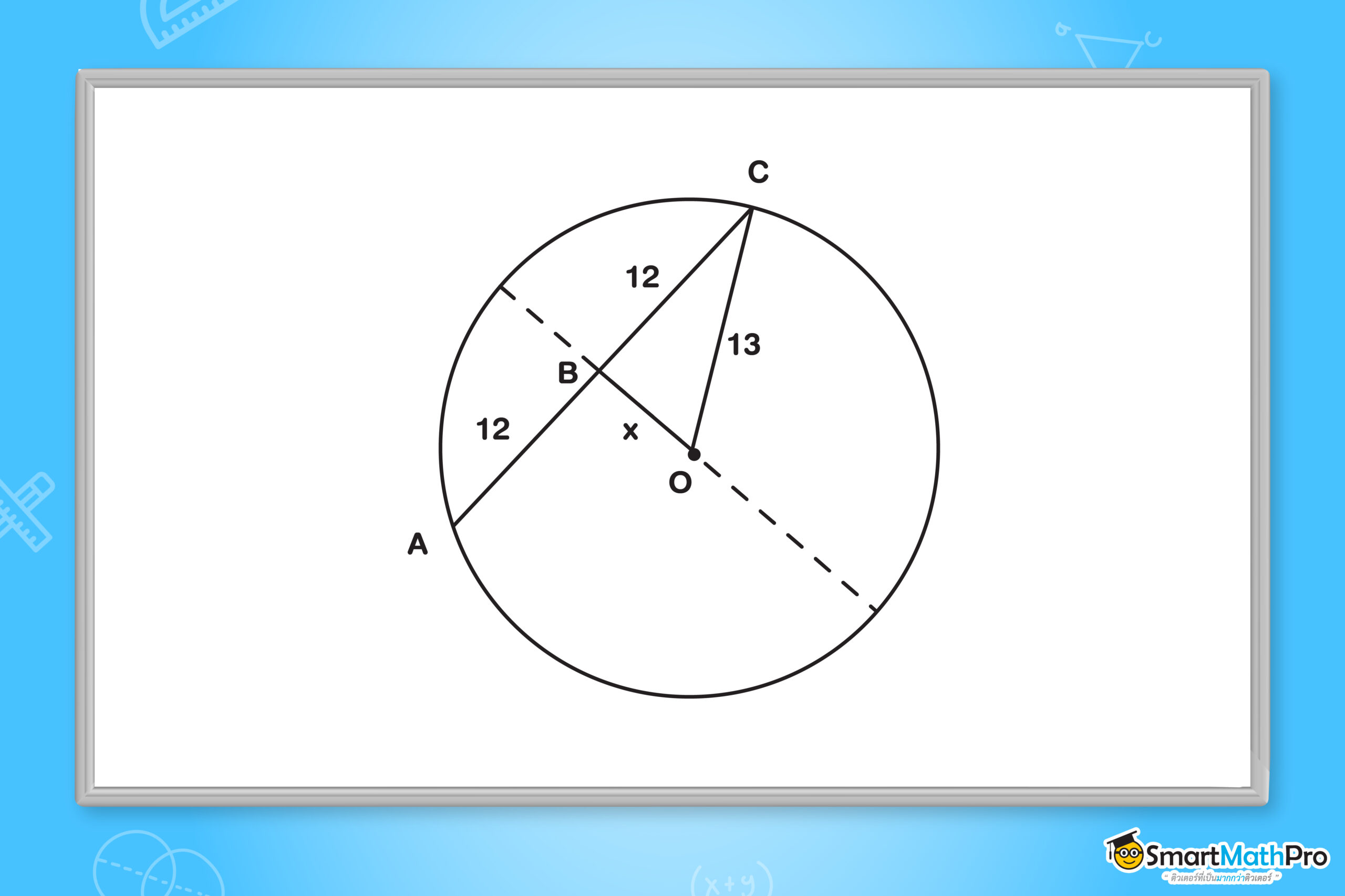
วิธีทำ
จาก ทฤษฎีบทที่ 5 ส่วนของเส้นตรงที่ลากจากจุดศูนย์กลางมาแบ่งครึ่งคอร์ดจะตั้งฉากกับคอร์ด
จะได้ว่า C\widehat{B}O= 90^{\circ}
จากทฤษฎีบทพีทาโกรัส จะได้
BO^{2}+BC^{2}=CO^{2}
x^{2}+12^{2}=13^{2}
x^{2}=13^{2}-12^{2}
x^{2}=25
x=-5, 5
เนื่องจาก x เป็นความยาวของ \overline{BO}
ดังนั้น x=5
ตอบ x=5
เส้นสัมผัสของวงกลม
มาถึงหัวข้อสุดท้ายกันแล้วนั่นก็คือเส้นสัมผัสวงกลมและรัศมีนั่นเอง ซึ่งหัวข้อนี้มีทฤษฎีบทที่น่าสนใจดังนี้
ทฤษฎีบทวงกลมที่ 7
เส้นสัมผัสวงกลมจะตั้งฉากกับรัศมีของวงกลมที่จุดสัมผัส
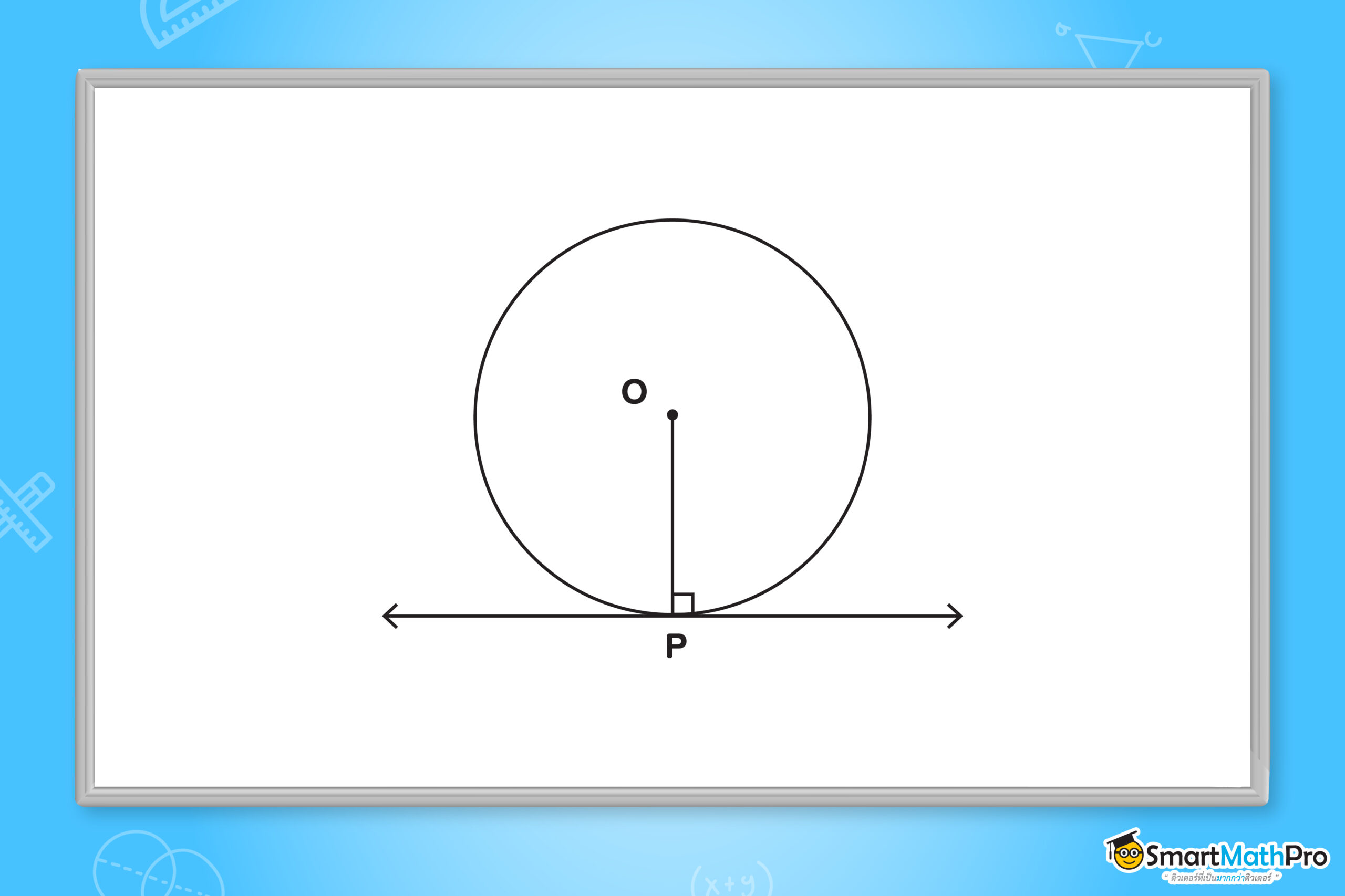
ถ้าเราลากเส้นตรงไปสัมผัสกับวงกลม โดยที่จุด P เป็นจุดสัมผัสดังรูป เราจะเรียกเส้นตรงนั่นว่า เส้นสัมผัส
และมุมที่เกิดจากเส้นสัมผัสและรัศมี \overline{OP} จะเป็นมุมฉากเสมอ
ลองสังเกตดูกันนะว่า เส้นสัมผัสจะตัดผ่านวงกลมเพียงแค่จุดเดียวซึ่งก็คือจุดสัมผัส แต่เมื่อเราลากเส้นตรงเส้นหนึ่งผ่านวงกลมแล้วได้จุดตัด 2 จุด เราจะเรียกว่าเส้นตรงนั้นว่า เส้นตัด
น้อง ๆ บางคนอาจจะคิดว่าไม่สำคัญหรอก ทฤษฎีบทที่ 7 ก็แค่ทฤษฎีบทเล็ก ๆ แต่ที่จริง ๆ แล้วเป็นทฤษฎีบทที่เจอได้
ค่อนข้างบ่อย และยังสามารถใช้ได้ในระดับชั้น ม.ปลายด้วยย
ทฤษฎีบทวงกลมที่ 8
ส่วนของเส้นตรง 2 เส้น ที่ลากจากจุดจุดหนึ่งภายนอกวงกลมมาสัมผัสวงกลมวงเดียวกันจะยาวเท่ากัน
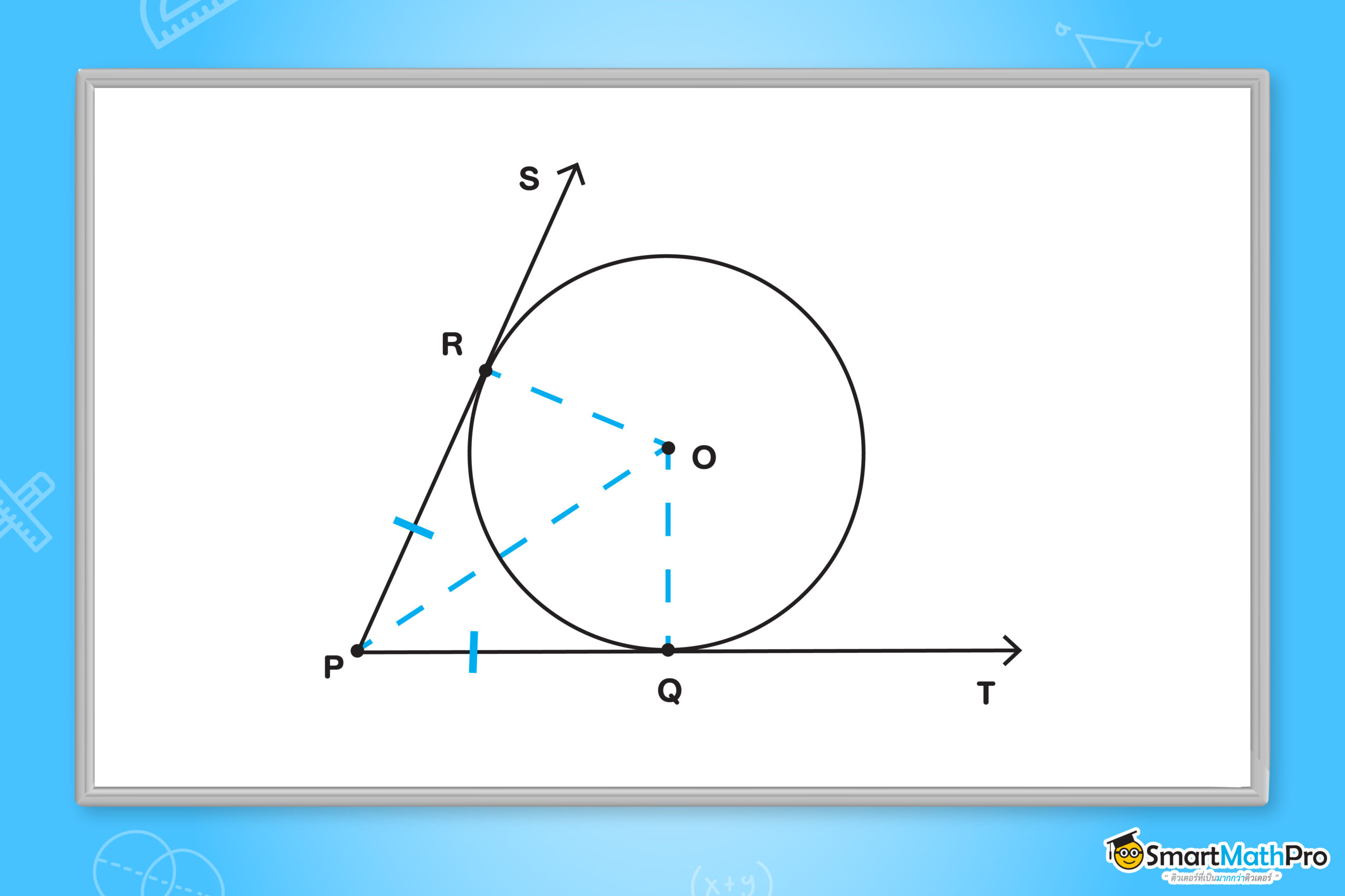
กำหนดให้จุด P เป็นจุดที่อยู่นอกวงกลม ลากเส้นจากจุด P มาสัมผัสวงกลมที่จุด R และจุด Q
จะได้
- P\widehat{R}O = P\widehat{Q}O = 90^{\circ} (จากทฤษฎีบทที่ 7 ที่ได้อธิบายไป)
- OP = OP (เป็นส่วนของเส้นตรงเดียวกัน)
- OR = OQ (รัศมีของวงกลม)
จากเหตุผลทั้ง 3 ข้อนี้ทำให้ \Delta POR และ \Delta POQ เป็นรูปสามเหลี่ยมที่เท่ากันทุกประการแบบด้าน-มุม-ด้านนั่นเอง
เราจะได้ว่า PR = PQ เพราะเป็นด้านที่สมนัยกัน ตามรูปและทฤษฎีบทข้างต้นเลย
ข้อควรระวัง
หากน้อง ๆ จะใช้ทฤษฎีบทนี้คือเส้นที่ลากจากจุดนอกวงกลมจะต้องเป็นเส้นสัมผัสวงกลมเท่านั้นนะ หากลากเส้นจาก
จุดนอกวงกลมผ่านวงกลมแล้วกลายเป็นเส้นตัดวงกลม (มีจุดตัด 2 จุด) จะไม่สามารถใช้ทฤษฎีบทนี้ได้
ทฤษฎีบทวงกลมที่ 9
มุมที่เกิดจากคอร์ดและเส้นสัมผัสวงกลมที่จุดสัมผัส จะมีขนาดเท่ากับขนาดของมุมในส่วนโค้งของวงกลมที่อยู่ตรงข้ามกับคอร์ดนั้น
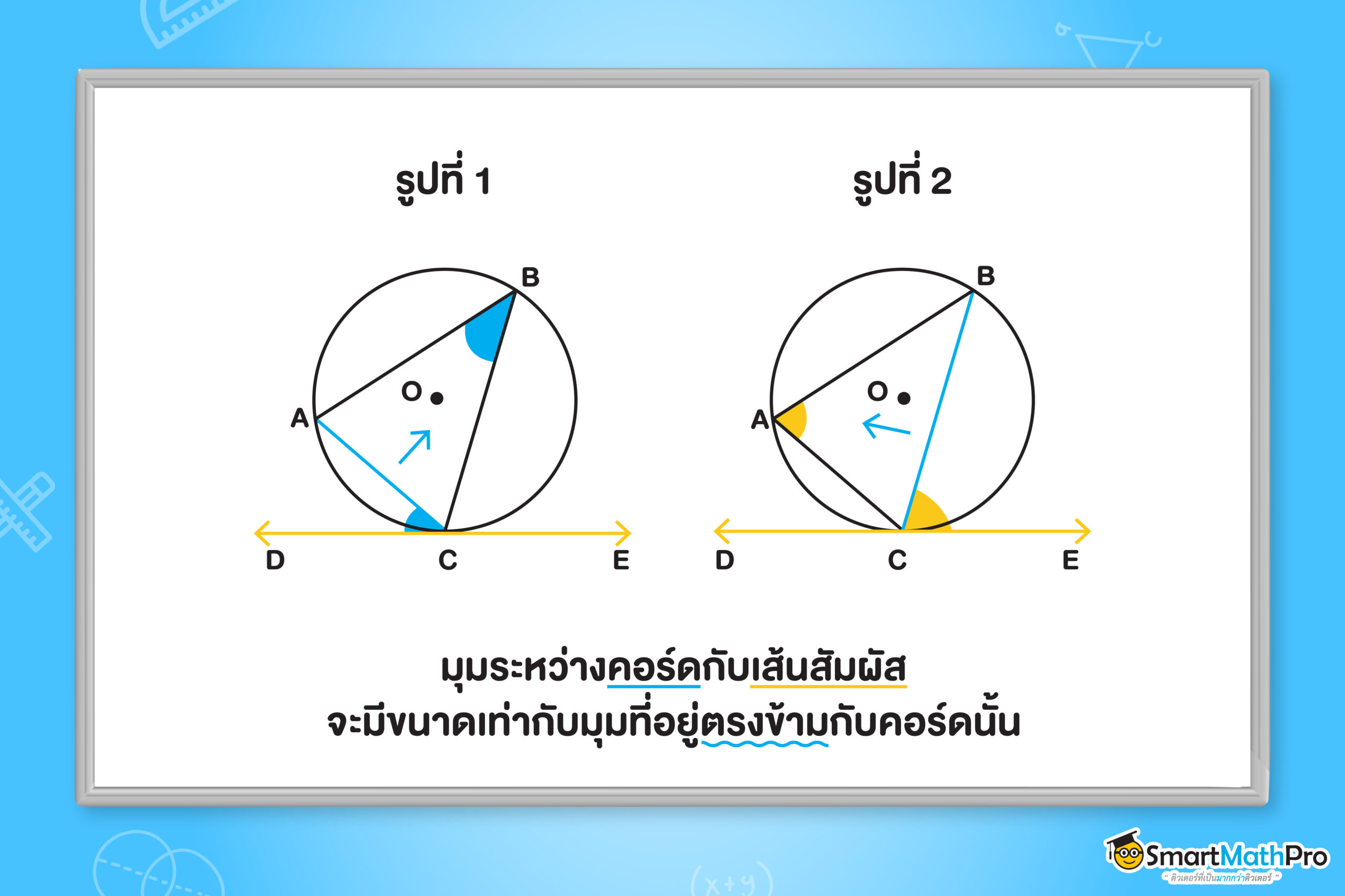
ลองสังเกตรูปที่ 1 กัน จากรูปเนี่ยเราจะเห็นว่า A\widehat{C}D มีแขนของมุมข้างหนึ่งเป็นเส้นสัมผัสวงกลมที่ผ่านจุด C กับ \overline{AC} ซึ่งเป็นคอร์ดของวงกลม O และมุมในส่วนโค้งที่อยู่ตรงข้ามคอร์ด \overline{AC} ก็คือ A\widehat{B}C จากทฤษฎีบทกำลังจะบอกว่า A\widehat{C}D = A\widehat{B}C
จากนั้นมาดูรูปที่ 2 จะได้ว่า B\widehat{C}E มีแขนของมุมข้างหนึ่งเป็นเส้นสัมผัสวงกลมที่ผ่านจุด C กับ \overline{BC} ซึ่งเป็นคอร์ดของวงกลม O และมุมในส่วนโค้งที่อยู่ตรงข้ามคอร์ด \overline{BC} ก็คือ C\widehat{A}B จากทฤษฎีบทกำลังจะบอกว่า
B\widehat{C}E = C\widehat{A}B
ข้อสังเกต
ให้น้อง ๆ สังเกตคอร์ดตามภาพให้ดี ว่ามุมที่เราได้มาในตอนตอนติดกับคอร์ดเส้นใด จากนั้นอีกมุมหนึ่งที่มีขนาด
เท่ากัน จะอยู่ตรงข้ามกับคอร์ดนั้น โดยสังเกตได้จากลูกศรที่พี่เขียนไว้ให้ในรูปข้างต้น
ตัวอย่างที่ 3
จากวงกลม O และเส้นสัมผัสที่กำหนดให้ จงหาค่าของ x
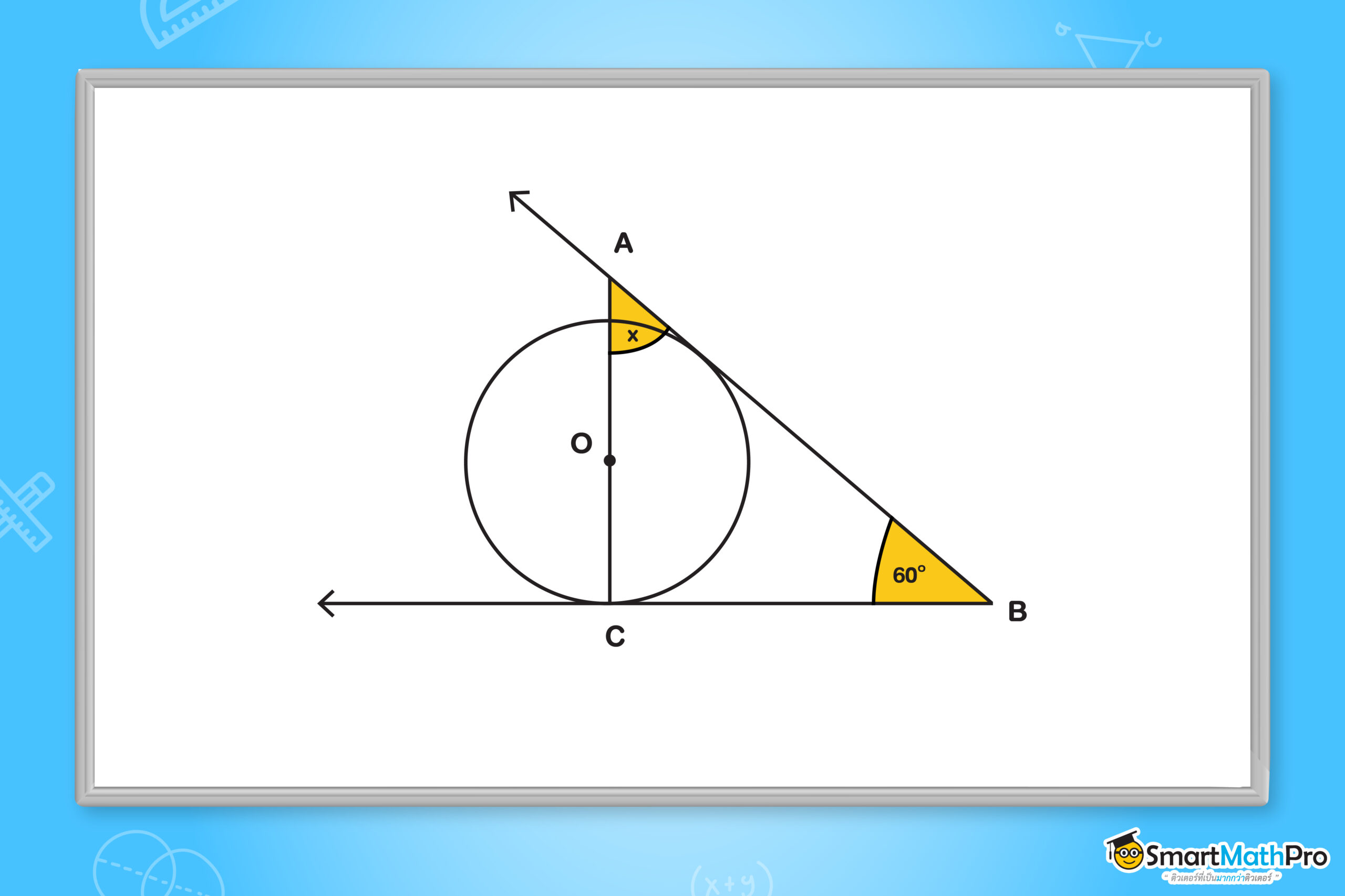
วิธีทำ
เนื่องจาก \overrightarrow{BC} เป็นเส้นสัมผัส
และ ทฤษฎีบทที่ 7 เส้นสัมผัสวงกลมจะตั้งฉากกับรัศมีของวงกลมที่จุดสัมผัส
จะได้ A\widehat{C}B = 90^{\circ}
จากผลรวมของขนาดของมุมภายในรูปสามเหลี่ยมเท่ากับ 180^{\circ}
จะได้ C\widehat{A}B= 180-(90+60)=30^{\circ}
ตอบ x=30^{\circ}
ดูคลิปติว วงกลม ม.3
ติดตามคลิปติวฟรีอื่น ๆ จากพี่ปั้น ได้ทาง YouTube Channel : SmartMathPro
อ่านมาจนถึงตรงนี้ พี่ว่าหลายคนคงแอบปาดเหงื่อให้กับทฤษฎีบทวงกลมที่มีเยอะมากกันอยู่ใช่ไหม แต่พี่เชื่อนะว่า ถ้า
น้อง ๆ ทบทวนเนื้อหาและฝึกทำโจทย์เรื่องวงกลมอยู่บ่อย ๆ ก็จะเข้าใจมากขึ้น ทำโจทย์ได้คล่องขึ้น พร้อมไปอัปคะแนนสอบกลางภาคแน่นอนน (และพี่ก็มีแบบฝึกหัดมาแจกฟรีให้ทุกคนด้วย ไปโหลดมาฝึกทำกันได้เลยย >>> แจกฟรีแบบฝึกหัดวงกลม ม.3
ส่วนใครที่ยังมีจุดที่สงสัยในบทวงกลม รวมถึงเนื้อหาอื่น ๆ ของคณิต ม.3 และต้องการคนช่วยไกด์เนื้อหาให้เข้าใจมากขึ้น พี่ขอแนะนำคอร์สติวคณิต ม.3 จาก SmartMathPro เลยย คอร์สนี้มีทั้งเนื้อหาของทั้งเทอม 1 และเทอม 2 ครบทุกบท ซึ่งพี่จะปูพื้นฐานให้แบบละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. พร้อมพาตะลุยโจทย์และแบบฝึกหัดจำนวนมาก โดยเริ่มจากง่ายไปจนถึงระดับข้อสอบแข่งขันจากสนามต่าง ๆ แถมยังมี Quiz ทบทวนความเข้าใจแต่ละบทให้ด้วยน้า ดังนั้นใครที่พื้นฐานไม่แน่นก็เรียนได้ ไม่ต้องกังวลเลยว่าจะเรียนไม่ทัน !!
แต่ถ้าโรงเรียนของน้อง ๆ สอนไม่ตรงตามคอร์สที่มี ก็สามารถเลือกเรียนแบบแยกบทได้เลยย เริ่มต้นเพียง 360 บาทเท่านั้น ใครสนใจดูรายละเอียดเพิ่มเติม คลิก ได้เลยน้าา
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สรุปคณิตศาสตร์ “ความคล้าย ม.3” พร้อมแจกโจทย์ปัญหาและเฉลยฟรี !!
สรุป แยกตัวประกอบพหุนามที่มีดีกรีสูงกว่าสอง ม.3 พร้อมโจทย์+เฉลย
สรุป อสมการเชิงเส้นตัวแปรเดียว ม.3 พร้อมแจกโจทย์และเฉลย
สรุป สมการกำลังสองตัวแปรเดียว ม.3 พร้อมแจกโจทย์ฟรี !!
สถิติ ม.3 สรุปเนื้อหาคณิตม.ต้นหลักสูตรใหม่ พร้อมแจกโจทย์ให้ลองทำ !
สรุป ฟังก์ชันกำลังสอง (พาราโบลา) ม.3 พร้อมแจกสูตรและโจทย์ฟรี
ตรีโกณมิติ ม.3 สรุปเนื้อหาพร้อมโจทย์แบบจัดเต็ม จบในที่เดียว !
บทความ แนะนำ
คณิตศาสตร์ ม.ต้น (ม.1 ม.2 ม.3) เรียนอะไรบ้าง ? อัปเดตล่าสุดจาก สสวท.
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
Twitter : @PanSmartMathPro
Tiktok : @pan_smartmathpro
