
อย่างที่หลายคนรู้กันว่า ตรรกศาสตร์ ที่เราเรียนกันในคณิต ม.4 เทอม 1 เป็นเรื่องเกี่ยวกับการใช้เหตุผล, การพิสูจน์เรื่องต่าง ๆ โดยอาศัยหลักทางคณิตศาสตร์เข้ามาช่วย แต่ถ้าใครไม่คุ้น หรือนึกภาพไม่ออกก็ไม่เป็นไร วันนี้พี่เตรียมสรุปเนื้อหามาให้ทุกคนแล้วว มีตั้งแต่ความหมาย เช่น ประพจน์ คือ, สัจนิรันดร์ คือ, การอ้างเหตุผล คือ และเรื่องอื่น ๆ แถมยังมีตัวอย่างโจทย์พร้อมคลิปติวเรื่องตรรกศาสตร์มาให้ด้วยน้า ถ้าใครอ่านจบและฝึกทำโจทย์บ่อย ๆ ก็สามารถนำไปใช้สอบได้เลยยย
สนใจหัวข้อไหน ... กดอ่านเลย
Toggleตรรกศาสตร์
ประพจน์
ประพจน์ (statement) คือ ประโยคหรือข้อความที่เป็น “จริง” หรือ “เท็จ” อย่างใดอย่างหนึ่งเท่านั้น
เรียก จริง (True: katex is not defined) หรือ เท็จ (False: katex is not defined) ว่า ค่าความจริง (truth value) ของประพจน์
ตัวอย่างที่ 1 ประโยคหรือข้อความต่อไปนี้เป็นประพจน์หรือไม่ ถ้าเป็นประพจน์จงบอกค่าความจริงของประพจน์
- พระอาทิตย์ขึ้นทางทิศตะวันออก
ตอบ เป็นประพจน์ มีค่าความจริงเป็นจริง katex is not defined - 3 + 2 = 6
ตอบ เป็นประพจน์ มีค่าความจริงเป็นเท็จ katex is not defined - katex is not defined เป็นจำนวนนับ
ตอบ ไม่เป็นประพจน์
ข้อสังเกต
ประพจน์จะเป็นประโยคที่อยู่ในรูปบอกเล่าหรือปฏิเสธก็ได้ และจะต้องมีค่าความจริงเดียวเท่านั้น
การเชื่อมประพจน์
ในชีวิตประจำวันน้อง ๆ จะพบประโยคที่ได้จากการเชื่อมกันมากกว่าหนึ่งประโยค โดยในบทนี้ตัวเชื่อมที่น้อง ๆ จะเจอ ได้แก่ “และ” “หรือ” “ถ้า…แล้ว…” “ก็ต่อเมื่อ” หรือพบประโยคซึ่งเปลี่ยนแปลงมาจากประโยคเดิม โดยเติมคำว่า “ไม่” เข้าไป ซึ่งคำทั้งหมดนี้เราจะเรียกว่า ตัวเชื่อม (connective) ทั้งหมดเลย
ประโยคที่มีตัวเชื่อมจะมีตัวอย่างดังนี้
- 2 เป็นจำนวนคู่ และ 1 เป็นจำนวนคี่
- ถ้า 3 เป็นจำนวนตรรกยะ แล้ว katex is not defined เป็นจำนวนอตรรกยะ
- รูปสามเหลี่ยมสองรูปคล้ายกัน ก็ต่อเมื่อ รูปสามเหลี่ยมสองรูปนั้นมีขนาดของมุมเท่ากันเป็นคู่ ๆ สามคู่
ถ้า katex is not defined และ katex is not defined เป็นประพจน์ใด ๆ แล้วการเชื่อมประพจน์ด้วยตัวเชื่อม “และ” “หรือ” “ถ้า…แล้ว…” “ก็ต่อเมื่อ” “ไม่”
จะมีการใช้สัญลักษณ์
- katex is not defined และ katex is not defined เขียนแทนด้วย katex is not defined
- katex is not defined หรือ katex is not defined เขียนแทนด้วย katex is not defined
- ถ้า katex is not defined แล้ว katex is not defined เขียนแทนด้วย katex is not defined
- นิเสธของ katex is not defined เขียนแทนด้วย katex is not defined
และจะมีค่าความจริง ดังนี้
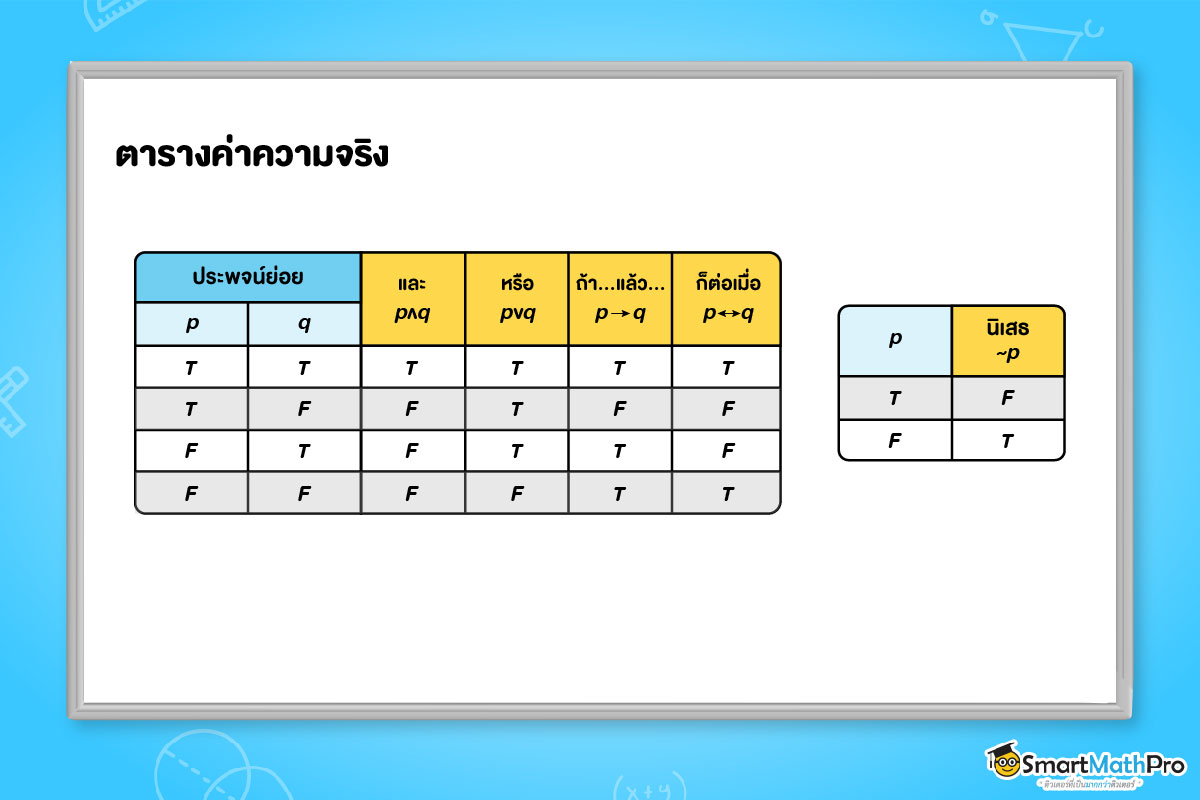
การหาค่าความจริงของประพจน์
จากตารางค่าความจริงในหัวข้อก่อนหน้านี้ ที่มีตัวเชื่อมแบบต่าง ๆ ที่เราเคยกล่าวมาแล้ว เมื่อโจทย์กำหนดค่าความจริงของประพจน์หนึ่งมา น้อง ๆ จะใช้ความรู้นี้เพื่อหาค่าความจริงของประพจน์ย่อยได้ ดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 2 กำหนดให้ katex is not defined และ katex is not defined เป็นประพจน์ที่มีค่าความจริงเป็น จริง และ เท็จ ตามลำดับ จงหาค่าความจริงของ katex is not defined
วิธีทำ katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
การสร้างตารางค่าความจริง
เมื่อโจทย์ไม่ได้กำหนดค่าความจริงของประพจน์ย่อยมาให้ แต่เราต้องการหาความจริงของประพจน์ใหญ่ ๆ ที่มีตัวเชื่อมอยู่ในนั้นด้วยแล้ว เราสามารถใช้ตารางค่าความจริง เพื่อวิเคราะห์ค่าความจริงของประพจน์ว่าเป็นจริงหรือเท็จในแต่ละกรณีได้ โดยเราจะมองว่า katex is not defined และ katex is not defined เป็นประพจน์ใด ๆ ซึ่งเราจะต้องสมมติค่าความจริงของ katex is not defined และ katex is not defined ทุกกรณี
โดย
- ถ้ามีประพจน์เดียวคือ katex is not defined จะมีกรณีในตารางค่าความจริงทั้งสิ้น 2 กรณี
- ถ้ามี 2 ประพจน์คือ katex is not defined และ katex is not defined จะมีกรณีในตารางค่าความจริงทั้งสิ้น 4 กรณี
- ถ้ามี 3 ประพจน์คือ katex is not defined และ katex is not defined จะมีกรณีในตารางค่าความจริงทั้งสิ้น 8 กรณี
ตัวอย่างที่ 3 กำหนดให้ katex is not defined และ katex is not defined เป็นประพจน์ จงสร้างตารางค่าความจริงของ katex is not defined
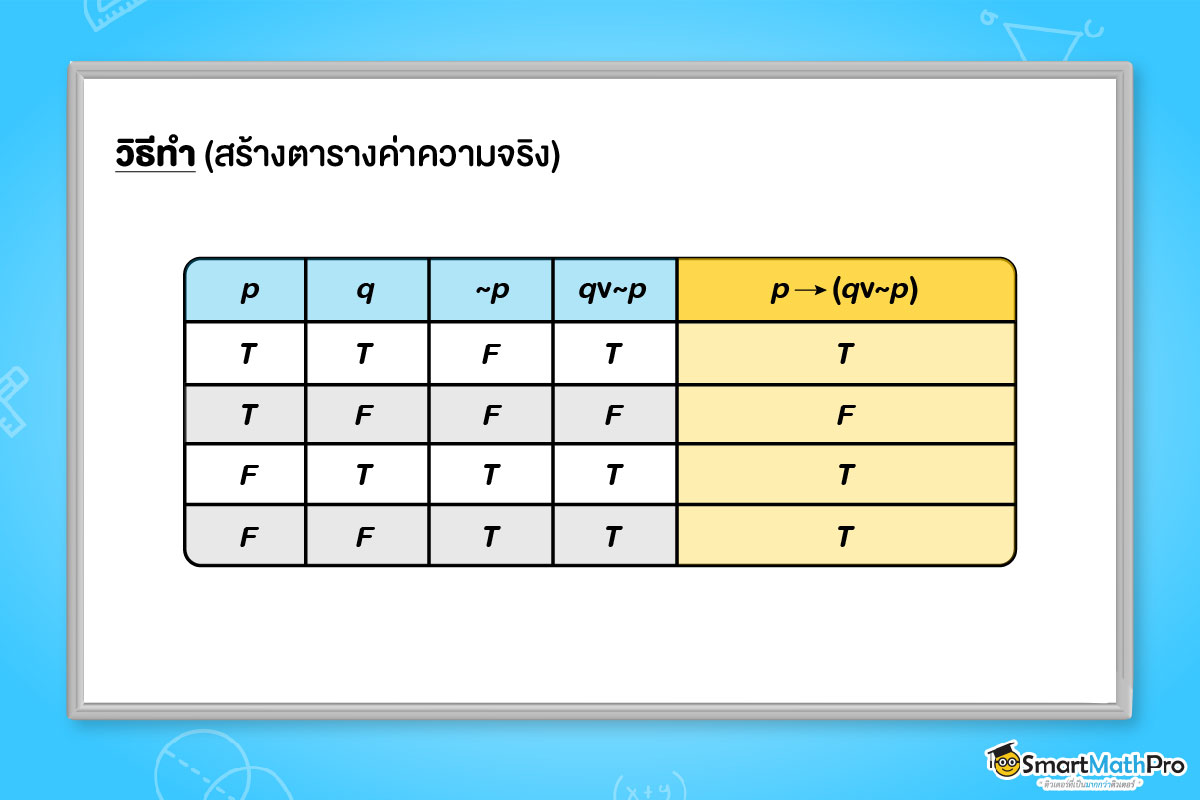
โจทย์บางข้อที่มีความซับซ้อนมากขึ้น โจทย์อาจไม่กำหนดค่าความจริงของประพจน์ย่อยมาให้ทุกตัว แต่เราจะต้องหาค่าความจริงของประพจน์ที่ใหญ่ขึ้นก้อนนั้น เช่น โจทย์ต้องการให้หาค่าความจริงของ katex is not defined แต่เราทราบค่าความจริงของประพจน์ย่อย katex is not defined เพียงตัวเดียว และไม่ทราบค่าความจริงของประพจน์ย่อย katex is not defined เลย มีวิธีการทำได้โดยให้น้อง ๆ ลองพิจารณาค่าความจริงของประพจน์ด้านล่างนี้ แต่ไม่ต้องท่องจำนะ !! ให้ลองทำความเข้าใจ โดยนำความรู้เรื่องตารางค่าความจริงก่อนหน้านี้มาใช้ด้วย ดังนี้

รูปแบบของประพจน์ที่สมมูลกัน
ถ้าน้อง ๆ สร้างตารางค่าความจริงแล้วพบว่ามีประพจน์สองรูปแบบที่มีค่าความจริงตรงกันทุกกรณี เราจะสามารถนำสองประพจน์นั้นไปใช้แทนกันได้เลย เพราะมันเหมือนกันเลย !! โดยเรียกรูปแบบของประพจน์ทั้งสองว่าเป็นรูปแบบของประพจน์ที่สมมูลกัน
เช่น katex is not defined กับ katex is not defined สองประพจน์นี้สมมูลกัน เพราะเมื่อสร้างตารางค่าความจริงแล้วจะมีค่าความจริงเหมือนกันแบบกรณีต่อกรณี ดังนั้นเราจะหยิบเอา katex is not defined หรือ katex is not defined ตัวไหนไปใช้ก็ได้ มันสามารถใช้แทนกันได้เลย
โดยน้อง ๆ สามารถตรวจสอบว่าประพจน์ทั้งสองสมมูลกันหรือไม่ ทำได้ 2 วิธี คือ
- สร้างตารางค่าความจริง
- ใช้รูปแบบของประพจน์ที่สมมูลกัน
วิธีที่ 1 สร้างตารางค่าความจริง
ประพจน์ที่สมมูลกันจะมีค่าความจริงเหมือนกันกรณีต่อกรณี
เช่น พิจารณาตารางค่าความจริงของ katex is not defined และ katex is not defined
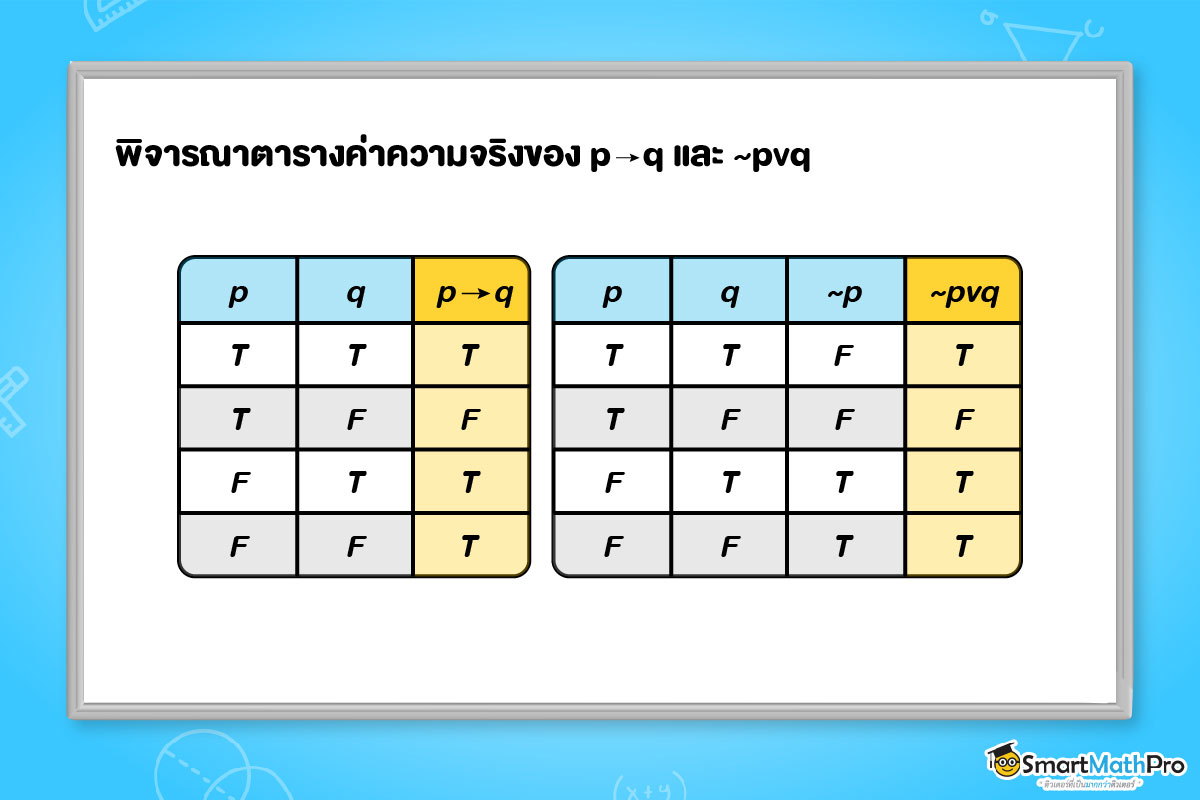
น้อง ๆ จะเห็นว่า จากตารางค่าความจริง ในช่องสุดท้ายค่าความจริงของ katex is not defined และ katex is not defined ตรงกันทุกกรณี แบบกรณีต่อกรณี
เราจึงสรุปได้ว่า katex is not defined และ katex is not defined เป็นรูปแบบของประพจน์ที่สมมูลกัน
วิธีที่ 2 ใช้รูปแบบประพจน์ที่สมมูลกัน
หากประพจน์ก้อนหนึ่งใหญ่มาก ๆ การสร้างตารางก็จะต้องใช้เวลามากตามไปด้วย และต้องใช้ความรอบคอบอย่างมากในการใส่ค่าความจริงลงไปในแต่ละช่องของตาราง เพราะถ้าใส่ค่าความจริงผิดแม้แต่ช่องเดียว ก็อาจทำให้คำตอบของเราออกมาผิดได้เลยทันที ดังนั้นพี่จึงแนะนำให้น้อง ๆ ใช้รูปแบบของประพจน์ที่สมมูลกันด้านล่างนี้ไปใช้ในการจัดรูป เพื่อดูว่าเราสามารถจัดรูปให้ประพจน์สองก้อนนั้นมีหน้าตาเหมือนกันได้หรือไม่ ซึ่งถ้าสามารถจัดรูปให้เหมือนกันได้ แสดงว่าประพจน์สองประพจน์นั้นสมมูลกัน

ตัวอย่างที่ 4 กำหนดให้ katex is not defined และ katex is not defined เป็นประพจน์
จงพิจารณาว่าประพจน์ katex is not defined และ katex is not defined สมมูลกันหรือไม่
วิธีทำ
katex is not defined
katex is not defined
katex is not defined
katex is not defined
ดังนั้น katex is not defined
น้อง ๆ จะเห็นว่าถ้าเราสามารถจัดรูปสองประพจน์ให้มีหน้าตาเหมือนกันได้ โดยใช้รูปแบบของประพจน์ที่สมมูลกัน นั่นคือประพจน์สองประพจน์นั้นสมมูลกัน
สัจนิรันดร์
สัจนิรันดร์ คือ รูปแบบของประพจน์ที่มีค่าความจริงเป็นจริงทุกกรณี
เรานิยมตรวจสอบว่ารูปแบบประพจน์นั้นเป็นสัจนิรันดร์หรือไม่ด้วย 2 วิธีต่อไปนี้
- สร้างตารางค่าความจริง
- หาข้อขัดแย้ง
วิธีที่ 1 สร้างตารางค่าความจริง
เราจะใช้วิธีการสร้างตารางค่าความจริงเหมือนที่น้อง ๆ เคยทำมาในหัวหน้าก่อนหน้านี้เลยนะ เพื่อพิจารณาว่าค่าความจริงที่ได้ในช่องขวาสุดเป็นจริงทั้งหมดหรือไม่ ถ้าเป็นจริงทั้งหมดเลยไม่ว่าประพจน์ย่อย katex is not defined จะมีค่าความจริงเป็นอะไร ก็จะได้ว่าประพจน์นั้นเป็นสัจนิรันดร์
ตัวอย่างที่ 5 จงตรวจสอบว่ารูปแบบของประพจน์ katex is not defined เป็นสัจนิรันดร์หรือไม่
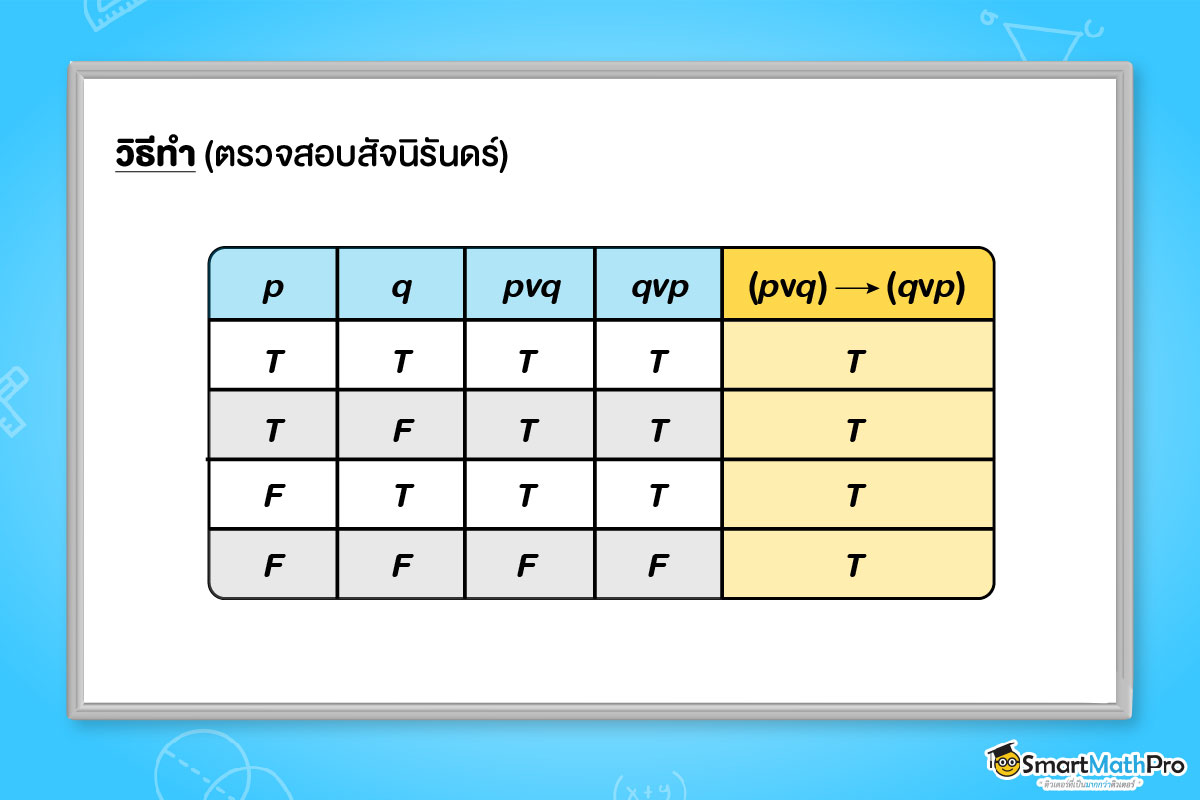
ดังนั้น katex is not defined เป็นสัจนิรันดร์
เช่นเดียวกับการสร้างตารางค่าความจริงในหัวข้ออื่น ๆ มันมีข้อจำกัดที่ว่าเราอาจต้องใช้เวลามาก และต้องใช้ความรอบคอบ พี่ก็จะแนะนำให้น้อง ๆ ลองฝึกใช้การหาข้อขัดแย้งซึ่งเป็นวิธีถัดไปดูน้าา
วิธีที่ 2 หาข้อขัดแย้ง
วิธีการหาข้อขัดแย้ง เป็นวิธีการที่สมมติให้รูปแบบของประพจน์ที่ต้องการหามีค่าความจริงเป็นเท็จ ถ้าไม่เกิดข้อขัดแย้ง จะสรุปว่ารูปแบบของประพจน์ไม่เป็นสัจนิรันดร์ เพราะสามารถเป็นเท็จตามที่เรากำหนดตอนแรก แต่หากพบข้อขัดแย้งระหว่างที่พยายามทำให้ประพจน์มีค่าเป็นเท็จ แสดงว่ารูปแบบของประพจน์นั้นไม่สามารถเป็นเท็จได้ แปลว่าต้องเป็นจริงเสมอ จึงสรุปได้ว่ารูปแบบของประพจน์เป็นสัจนิรันดร์ นั่นเอง
ตัวอย่างที่ 6 กำหนดให้ katex is not defined และ katex is not defined เป็นประพจน์ จงตรวจสอบว่ารูปแบบของประพจน์ต่อไปนี้เป็นสัจนิรันดร์หรือไม่
1) katex is not defined
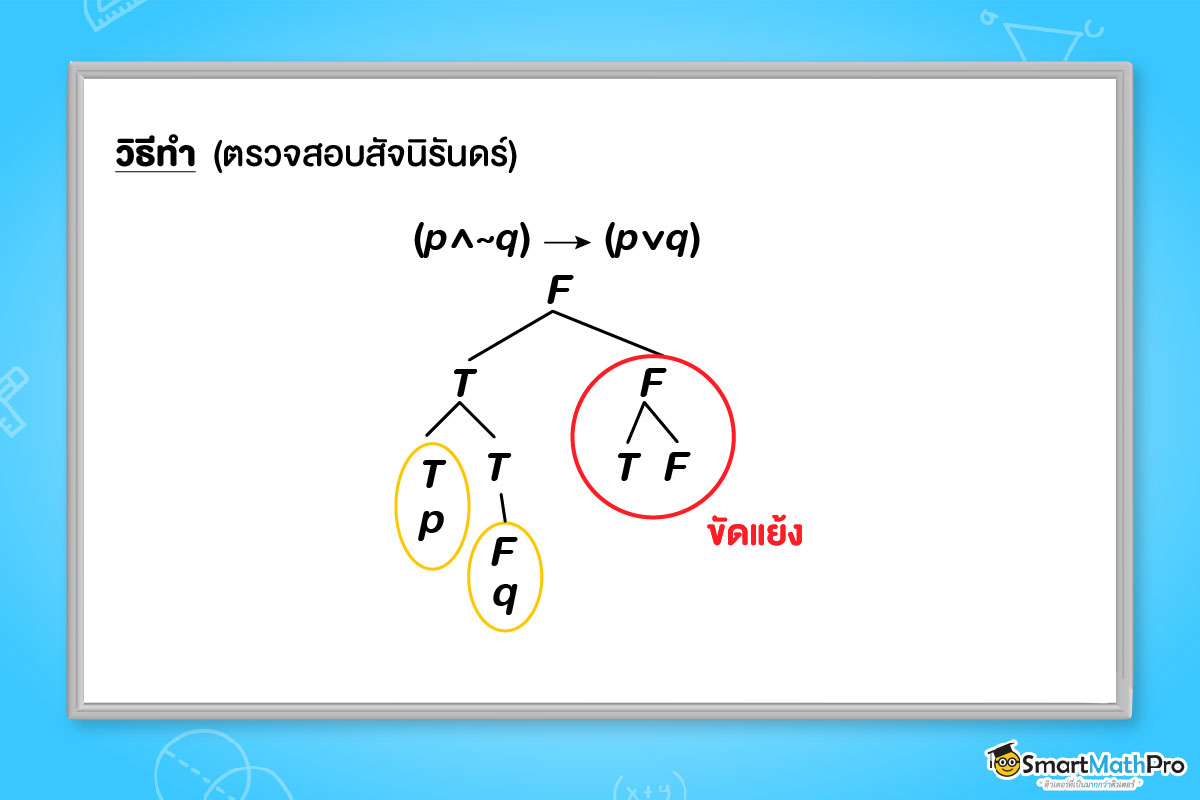
เนื่องจากเกิดข้อขัดแย้ง
ดังนั้น katex is not defined เป็นสัจนิรันดร์
2) katex is not defined
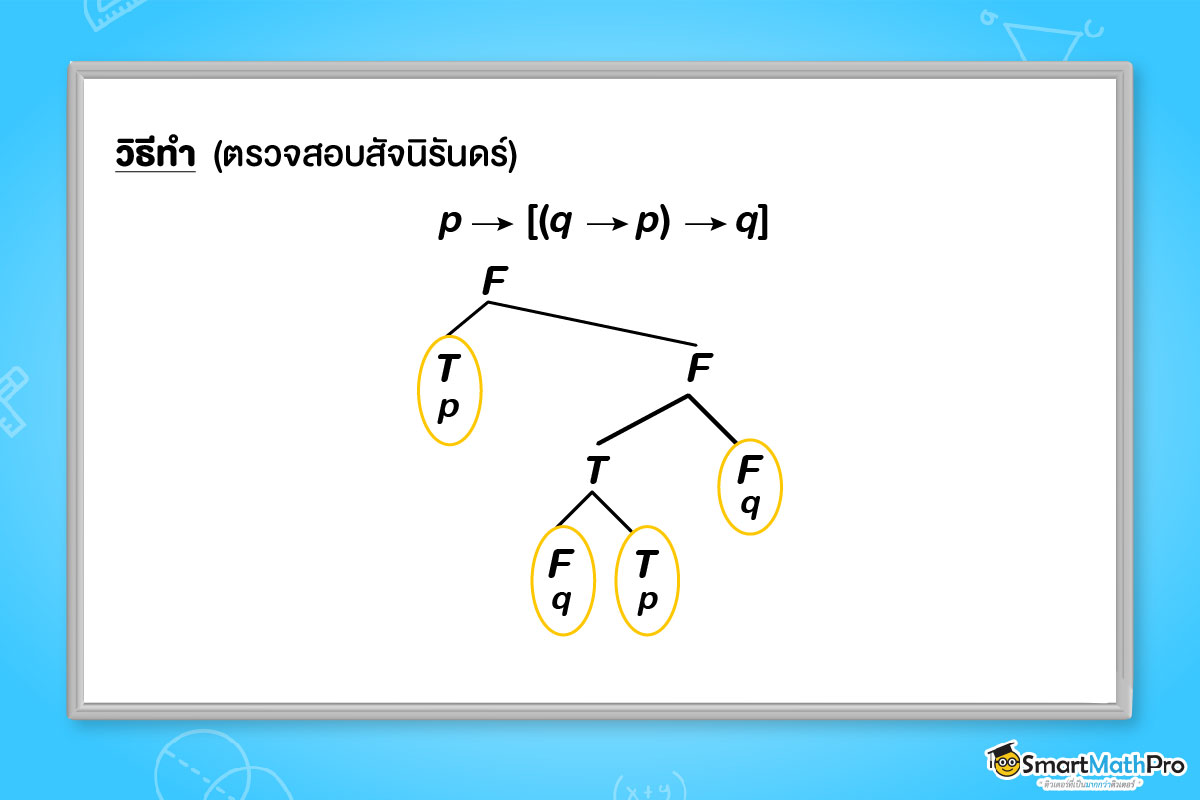
เนื่องจากไม่เกิดข้อขัดแย้ง
ดังนั้น katex is not defined ไม่เป็นสัจนิรันดร์
ก่อนจะขึ้นหัวข้อถัดไป พี่จะขอสรุปเกี่ยวกับการใช้การหาข้อขัดแย้งเพื่อตรวจสอบสัจนิรันดร์ให้เข้าใจง่าย ๆ ไว้ข้างล่างนี้ แต่จะขอความร่วมมือน้อง ๆ ว่า ขณะที่อ่านอยู่ ถ้ามีตรงไหนมีคำว่า “ไม่” ให้ส่ายหน้าแรง ๆ ตรงนั้นตอนอ่านด้วยนะ เป็นอรรถรส
มีข้อขัดแย้ง คือ เป็นสัจนิรันดร์
ไม่มีข้อขัดแย้ง คือ ไม่เป็นสัจนิรันดร์
การอ้างเหตุผล
ประกอบด้วย เหตุ katex is not defined และ ผล katex is not defined
การอ้างเหตุผล จะเชื่อมเหตุแต่ละตัวด้วย “และ” และเชื่อมจากเหตุไปผลด้วย “ถ้า…แล้ว…”
ได้เป็นรูปแบบของประพจน์ในรูป katex is not defined
การอ้างเหตุผลนี้สมเหตุสมผล (Valid) ก็ต่อเมื่อ รูปแบบของประพจน์เป็นสัจนิรันดร์
และไม่สมเหตุสมผล (Invalid) ก็ต่อเมื่อ รูปแบบของประพจน์ไม่เป็นสัจนิรันดร์
กล่าวคือ ในหัวข้อนี้เราจะตรวจสอบแบบเดียวกับที่ตรวจสอบสัจนิรันดร์เลย เพียงแค่เพิ่มขั้นตอนที่ 1 ตามตัวอย่างด้านล่างนี้มาเท่านั้นเองนะ
ตัวอย่างที่ 7 กำหนดให้ katex is not defined และ katex is not defined เป็นประพจน์ จงตรวจสอบว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่
เหตุ 1. katex is not defined
2. katex is not defined
3. katex is not defined
ผล katex is not defined
วิธีทำ
ขั้นที่ 1
ใช้เครื่องหมาย katex is not defined
เชื่อมเหตุเข้าด้วยกัน และใช้ katex is not defined เชื่อมส่วนที่เป็นเหตุและผล
จะได้รูปแบบของประพจน์ คือ katex is not defined
ขั้นที่ 2
ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่
โดย สมมติให้ katex is not defined เป็นเท็จ
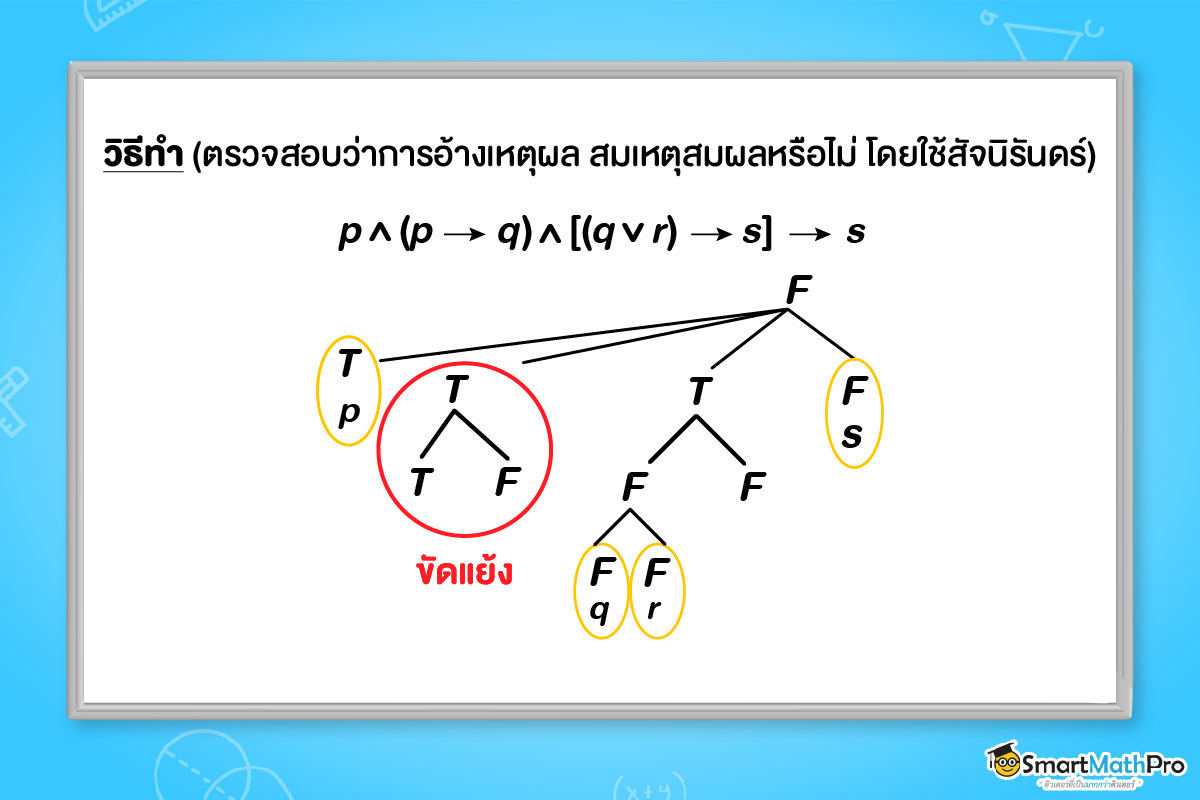
จากแผนภาพเกิดข้อขัดแย้ง แสดงว่า รูปแบบของประพจน์
katex is not defined เป็นสัจนิรันดร์
ดังนั้น การอ้างเหตุผลนี้สมเหตุสมผล
เหมือนเดิมเลยน้า ก่อนที่จะไปอ่านสรุปในกรอบด้านล่าง ขณะที่อ่านอยู่ ถ้ามีตรงไหนมีคำว่า “ไม่” ให้ส่ายหน้าแรง ๆ ตรงนั้นตอนอ่านด้วยนะ เอาให้ผีในห้องงงว่าอ่านอะไรอยู่
มีข้อขัดแย้ง คือ เป็นสัจนิรันดร์ แสดงว่าการอ้างเหตุผลนั้น สมเหตุสมผล
ไม่มีข้อขัดแย้ง คือ ไม่เป็นสัจนิรันดร์ แสดงว่าการอ้างเหตุผลนั้น ไม่สมเหตุสมผล
ประโยคเปิดและตัวบ่งปริมาณ
ให้น้อง ๆ ลองพิจารณาประโยค “เขาเป็นนักร้อง” ประโยคนี้เราจะยังไม่ทราบว่ามีค่าความจริงเป็นอะไร จนกว่าเราจะแทนชื่อใครสักคนลงไปในคำว่าเขา เช่น แทนชื่อพี่ปั้นลงไปจะได้ว่า “พี่ปั้นเป็นนักร้อง” เราถึงจะได้ว่าประโยคนี้เป็นเท็จนะ เพราะถึงพี่ปั้นจะร้องเพลงเพราะ แต่พี่ปั้นไม่ได้เป็นนักร้อง พี่ปั้นสอนคณิตศาสตร์ !! น้อง ๆ พอจะเข้าใจความหมายของประโยคเปิดกันแล้วใช่ไหม เราไปดูความหมายแบบทางการขึ้นอีกนิดกันดีกว่า
ประโยคเปิด
คือ ประโยคบอกเล่าหรือปฏิเสธที่มีตัวแปร ซึ่งจะไม่ทราบค่าความจริงจนกว่าจะแทนค่าลงในตัวแปร เช่น
ประโยคเปิด : katex is not defined
- แทน “katex is not defined” ด้วย “0” จะได้ “0<1” ซึ่งเป็นจริง
นั่นคือเป็นการแทนค่าตัวแปรที่ได้ค่าความจริงเป็นจริง - แทน “katex is not defined” ด้วย “2”จะได้ “2<1” ซึ่งเป็นเท็จ
นั่นคือเป็นการแทนค่าตัวแปรที่ได้ค่าความจริงเป็นเท็จ
หมายเหตุ โดยส่วนมากจะเขียนแทนประโยคเปิดด้วย katex is not defined
ตัวบ่งปริมาณ
ในทางตรรกศาสตร์ มี 2 ตัว คือ katex is not defined (for all) และ katex is not defined (for some)
- katex is not defined แทน สำหรับ katex is not defined ทุกตัว
- katex is not defined แทน สำหรับ katex is not defined บางตัว
เอกภพสัมพัทธ์ ในที่นี้หมายถึงเซตที่บอกขอบเขตของสิ่งที่จะพิจารณาประโยคเปิด เขียนแทนด้วย katex is not defined ซึ่งจะระบุสมาชิกเซต หรือเป็นสัญลักษณ์ดังนี้
- katex is not defined แทน เซตของจำนวนจริง
- katex is not defined แทน เซตของจำนวนตรรกยะ
- katex is not defined แทน เซตของจำนวนเต็ม
-
katex is not defined แทน เซตของจำนวนนับ
ประโยคเปิดที่มีตัวบ่งปริมาณ
คือ ข้อความที่ประกอบด้วยตัวบ่งปริมาณและประโยคเปิด ซึ่งจะกำหนดเอกภพสัมพัทธ์เอาไว้ด้วย
ข้อความต่อไปนี้อาจเขียนให้อยู่ในรูปสัญลักษณ์ได้
- สำหรับ katex is not defined ทุกตัว katex is not defined เมื่อเอกภพสัมพัทธ์เป็นเซตของจำนวนนับ
katex is not defined เมื่อ katex is not defined
หรือ katex is not defined
- สำหรับ katex is not defined บางตัว katex is not defined เมื่อเอกภพสัมพัทธ์เป็นเซตของจำนวนจริง
katex is not defined เมื่อ katex is not defined
หรือ katex is not defined
ข้อความข้างต้น น้อง ๆ จะเห็นว่า ถ้าเราเติมตัวบ่งปริมาณข้างหน้าประโยคเปิดจะได้เป็นประโยคเปิดที่มีตัวบ่งปริมาณ ซึ่งข้อความเหล่านี้เราสามารถหาค่าความจริงของมันได้ด้วย พี่จะลองใช้ประโยคในตัวอย่างก่อนหน้านี้มาลองหาค่าความจริงของมันกัน
- จาก katex is not defined
มีค่าความจริงเป็นจริง เนื่องจากเมื่อนำจำนวนจริงทุกจำนวน บวกศูนย์ แล้วจะได้ตัวมันเองเสมอ
- จาก katex is not defined
มีค่าความจริงเป็นจริง เนื่องจากเมื่อแทน katex is not defined ด้วย katex is not defined (ซึ่ง katex is not defined เป็นจำนวนจริง) จะได้ว่า katex is not defined ทำให้ได้สมการเป็นจริง
จากตัวอย่างข้างต้น จะเห็นว่า ถ้าเติมตัวบ่งปริมาณข้างหน้าประโยคเปิดแล้วจะได้ประพจน์ เนื่องจากเราสามารถหาค่าความจริงได้ โดยประโยคที่มีตัวบ่งปริมาณเหล่านี้จะมีค่าความจริงเป็นจริงหรือเท็จเพียงอย่างใดอย่างหนึ่งเท่านั้น
ค่าความจริงของประโยคที่มีตัวบ่งปริมาณ
การพิจารณาค่าความจริงของประโยคที่มีตัวบ่งปริมาณนั้น โดยทั่วไปจะพิจารณาแต่ละส่วนของประโยคที่มีตัวบ่งปริมาณดังนี้
- ส่วนที่ 1 ตัวบ่งปริมาณ
- ส่วนที่ 2 ประโยคเปิด
- ส่วนที่ 3 เอกภพสัมพัทธ์
กำหนดให้ katex is not defined เป็นประโยคเปิด และ katex is not defined เป็นเอกภพสัมพัทธ์ จะได้ว่า
katex is not defined
- มีค่าความจริงเป็นจริง ก็ต่อเมื่อ
แทนตัวแปร katex is not defined ใน katex is not defined ด้วยสมาชิกแต่ละตัวในเอกภพสัมพัทธ์ แล้วได้ประพจน์ที่มีค่าความจริงเป็นจริงทั้งหมด - มีค่าความจริงเป็นเท็จ ก็ต่อเมื่อ
แทนตัวแปร katex is not defined ใน katex is not defined ด้วยสมาชิกอย่างน้อยหนึ่งตัวในเอกภพสัมพัทธ์ แล้วได้ประพจน์ที่มีค่าความจริงเป็นเท็จ
katex is not defined
- มีค่าความจริงเป็นจริง ก็ต่อเมื่อ
แทนตัวแปร katex is not defined ใน katex is not defined ด้วยสมาชิกอย่างน้อยหนึ่งตัวในเอกภพสัมพัทธ์ แล้วได้ประพจน์ที่มีค่าความจริงเป็นจริง - มีค่าความจริงเป็นเท็จ ก็ต่อเมื่อ
แทนตัวแปร katex is not defined ใน katex is not defined ด้วยสมาชิกแต่ละตัวในเอกภพสัมพัทธ์ แล้วได้ประพจน์ที่มีค่าความจริงเป็นเท็จทั้งหมด
ตัวอย่างที่ 8 กำหนดเอกภพสัมพัทธ์ katex is not defined = {katex is not defined} จงหาค่าความจริงของประพจน์ต่อไปนี้
1. katex is not defined
วิธีทำ ให้ katex is not defined แทนประโยคเปิด katex is not defined เนื่องจาก
katex is not defined แทน katex is not defined เป็นจริง
katex is not defined แทน katex is not defined เป็นจริง
katex is not defined แทน katex is not defined เป็นจริง
ดังนั้น katex is not defined เป็นจริง เมื่อ katex is not defined = {katex is not defined}
2. katex is not defined
วิธีทำ ให้ katex is not defined แทนประโยคเปิด katex is not defined เนื่องจาก katex is not defined แทน katex is not defined เป็นเท็จ
ดังนั้น katex is not defined เป็นเท็จ เมื่อ katex is not defined = {katex is not defined}
3. katex is not defined
วิธีทำ ให้ katex is not defined แทนประโยคเปิด katex is not defined เนื่องจาก katex is not defined แทน katex is not defined เป็นจริง
ดังนั้น katex is not defined เป็นจริง เมื่อ katex is not defined = {katex is not defined}
4. katex is not defined
วิธีทำ ให้ katex is not defined แทนประโยคเปิด katex is not defined เนื่องจาก
katex is not defined แทน katex is not defined เป็นเท็จ
katex is not defined แทน katex is not defined เป็นเท็จ
katex is not defined แทน katex is not defined เป็นเท็จ
ดังนั้น katex is not defined เป็นเท็จ เมื่อ katex is not defined = {katex is not defined}
ข้อสังเกต
ถ้าเราอยากตรวจสอบว่า katex is not defined เป็นจริงหรือเท็จ ให้น้อง ๆ พยายามหา katex is not defined หนึ่งตัวที่นำไปแทนใน katex is not defined แล้วจะทำให้เป็นเท็จจะง่ายกว่า เพราะถ้ามี katex is not defined เพียงตัวเดียวที่ทำให้เป็นเท็จ katex is not defined จะเป็นเท็จเลยทันที
และถ้าเราอยากตรวจสอบว่า katex is not defined เป็นจริงหรือเท็จ ให้น้อง ๆ พยายามหา katex is not defined หนึ่งตัวที่นำไปแทนใน katex is not defined แล้วจะทำให้เป็นจริงจะง่ายกว่า เพราะถ้ามี katex is not defined เพียงตัวเดียวที่ทำให้เป็นจริง katex is not defined จะเป็นจริงเลยทันที
น้อง ๆ บางคนอาจสับสนว่าแล้วถ้าตัวบ่งปริมาณนั้นมีตัวเชื่อมอยู่ด้านนอก หรือมีตัวเชื่อมอยู่ด้านในประโยคเปิด พี่จะบอกว่ามันแตกต่างกันนะ วิธีการหาค่าความจริงก็แตกต่างกัน ตามตัวอย่างด้านล่างนี้เลย
ตัวอย่างที่ 9 กำหนดเอกภพสัมพัทธ์ katex is not defined= {katex is not defined} จงหาค่าความจริงของประพจน์ต่อไปนี้
1. katex is not defined
แนวคิด ให้น้อง ๆ พิจารณาค่าความจริงของ katex is not defined และ katex is not defined แยกกัน แล้วนำค่าความจริงที่ได้มาเชื่อมกันด้วยตัวเชื่อม katex is not defined
วิธีทำ ให้ katex is not defined และ katex is not defined แทนประโยคเปิด katex is not defined และ katex is not defined ตามลำดับ
- จะได้ว่า katex is not defined มีค่าความจริงเป็นจริง
เนื่องจาก katex is not defined แทน katex is not defined ซึ่งเป็นจริง
นั่นคือ katex is not defined
- จะได้ว่า katex is not defined มีค่าความจริงเป็นเท็จ เนื่องจาก
katex is not defined แทน katex is not defined ซึ่งเป็นเท็จ
katex is not defined แทน katex is not defined ซึ่งเป็นเท็จ และ
katex is not defined แทน katex is not defined ซึ่งเป็นเท็จ
นั่นคือ katex is not defined
จะได้ว่า katex is not defined
ดังนั้น katex is not defined มีค่าความจริงเป็นเท็จ
2. katex is not defined
แนวคิด ให้น้อง ๆ พิจารณาค่าความจริงโดยแทนค่า katex is not defined จาก katex is not defined ลงใน katex is not defined เป็นก้อนเดียวกันไปเลย
วิธีทำ ให้ katex is not defined แทนประโยคเปิด katex is not defined
เนื่องจาก
katex is not defined แทน katex is not defined ซึ่งเป็นเท็จ
katex is not defined แทน katex is not defined ซึ่งเป็นเท็จ
katex is not defined แทน katex is not defined ซึ่งเป็นเท็จ
ดังนั้น katex is not defined มีค่าความจริงเป็นเท็จ
สมมูลและนิเสธของประโยคที่มีตัวบ่งปริมาณ
สมมูล
- katex is not defined ก็ต่อเมื่อ katex is not defined
- katex is not defined ก็ต่อเมื่อ katex is not defined
นิเสธ
- katex is not defined
- katex is not defined
ถ้าน้อง ๆ จะกระจายนิเสธเข้าไป จะต้องกระจายไปที่ตัวบ่งปริมาณ แล้วอย่าลืมกระจายเข้าไปใน katex is not defined ด้วยน้าา
ตัวอย่างที่ 10 จงพิจารณาว่าประโยคในข้อต่อไปนี้สมมูลกันหรือไม่
- katex is not defined
สมมูลกัน เนื่องจาก katex is not defined - katex is not defined กับ katex is not defined
ไม่สมมูลกัน เนื่องจาก katex is not defined
ดูคลิปติวฟรี ตรรกศาสตร์ ม.4
ดูคลิปติวฟรีอื่น ๆ ได้ที่ YouTube : SmartMathPro
เป็นยังไงกันบ้างงง สำหรับเรื่อง “ตรรกศาสตร์ ม.4” ที่พี่เอามาฝากกันในวันนี้ ได้ความรู้กันไปแบบจุก ๆ เลยใช่มั้ยย ถ้าใครอยากเข้าใจมากขึ้น พี่แนะนำให้ฝึกทำโจทย์กันเยอะ ๆ เพราะจะได้ทบทวนเนื้อหาและความเข้าใจของตัวเองไปในตัว แถมยังใช้ต่อยอดในการเตรียมสอบเข้ามหาลัยฯ ได้อีกด้วย ซึ่งพี่ก็มีข้อสอบ ตรรกศาสตร์ ม.4 ในคลังข้อสอบให้ทุกคนได้ไปดาวน์โหลดมาฝึกทำเพียบบบบ !!
แต่ถ้าใครอ่านแล้วยังไม่เข้าใจก็ไม่เป็นไรน้าาาา พี่แนะนำว่าให้ทบทวนและฝึกทำโจทย์เป็นประจำ พอได้เจอโจทย์หลาย ๆ แบบก็จะทำให้เข้าใจในเนื้อหามากขึ้น แต่ถ้าใครยังกังวล กลัวว่าถ้าทบทวนเองแล้วจะไม่เข้าใจ จนทำให้เรียนบทอื่นต่อไม่ได้ อยากได้คนช่วยไกด์
พี่ขอแนะนำคอร์สติวคณิตศาสตร์ ม.4 – 6 แบบบุฟเฟต์สำหรับเสริมเกรด จาก SmartMathPro เลยย สมัครครั้งเดียวคุ้มมากกเรียนได้จนจบม.6 พร้อมส่วนลดสูงสุด 35% โดยในคอร์ส พี่ปูพื้นฐานละเอียด เจาะลึกเฉพาะบท อิงตามหลักสูตร สสวท. ใครพื้นฐานไม่ดีก็เรียนได้สบายมากใครสนใจดูรายละเอียดเพิ่มเติมก็ คลิก ได้เลย
บทความ แนะนำ
สำหรับน้อง ๆ ที่สนใจสอบถามข้อมูลเพิ่มเติม รวมถึงติดตามข่าวสารต่าง ๆ ที่อัปเดตอย่างเรียลไทม์ ได้ที่
Line : @smartmathpronews
FB : Pan SmartMathPro ติวคณิต By พี่ปั้น
IG : pan_smartmathpro
X : @PanSmartMathPro
Tiktok : @pan_smartmathpro
Lemon8 : @pan_smartmathpro
























